[ML] 7편 - Regression criteria(회귀 평가지표)와 Gradient Descent algorithm(경사하강법)

재로미·2021년 2월 16일
머신러닝
1

Machine Learning

목록 보기
7/7
post-custom-banner

Review : Linear regression

약 2~3편에 걸쳐서 linear regression, 즉 선형 회귀에 대해 공부했었다. 간단히 복습을 하자면, 회귀분석은 데이터 분석법 중 하나로, 주어진 데이터 사이에 나타나는 관계를 함수식으로 세워 통계적으로 추론하고 나아가 예측하는 분석법이다. 수치형 설명 변수 X와 연속형 숫자인 결과 변수 Y간에 선형 관계가 나타난다고 할 때 이를 가장 잘 표현할 수 있는 회귀계수를 추정하는 모델을 수립하는 것이라 할 수 있고, 수학적 표현은 아래와 같다.
linear_reg

yj^=fj(x)=w1jx1+w2jx2+⋯+bj=∑iwijxi+bj\hat{y_j} = f_j(x) = w_{1j}x_1 + w_{2j}x_2 + \cdots + b_j = \sum_iw_{ij}x_i + b_j

그리고 실제값과 추정값의 차를 제곱한 오차제곱합을 최소화하는 것이 선형회귀 분석의 목적이 될 수 있다고 하였다. 이렇게 수립한 회귀식이 얼마나 잘 적합한지, 다른 회귀식이나 방법으로 구축된 추정식을 비교하여 성능을 가늠할 수 있는 지표도 필요한데 대표적으로 MAE, MSE, RMSE, MSLE, RMSLE, 그리고 R2R^2가 있다.

회귀 성능 평가 척도

  • 평균제곱오차 - MSE (Mean Squared Error)

여러 지표들 중 대표적으로 사용되는 방법으로, 실제값과 예측값의 차이 즉 오차제곱합의 평균을 구하여 성능으로 삼는 것이다. 수식은 오차제곱합에 데이터 개수를 나눈 공식이다.

MSE=1N∑i=1N(yi−y^)2MSE = {1 \over N} \sum_{i=1}^N(y_i - \hat{y})^2
  • 평균절대오차 - MAE (Mean Absolute Error)

실제값과 추정치의 차이에 절댓값을 취한 후 이들을 더해 평균을 낸 것이다.

MAE=1N∑i=1N∣yi−y^∣MAE = {1 \over N} \sum_{i=1}^N |y_i - \hat{y}|
  • 제곱근평균제곱오차 - RMSE (Root Mean Squared Error)

오차들을 제곱하는 이유는 부호를 날려버리기 위함인데, 제곱을 함으로써 실제 오차들보다 값이 많이 커지는 특성이 있어 MSE에 루트를 씌운 척도도 있으며 이를 RMSE라고 부른다.

RMSE=MSE=1N∑i=1N(yi−y^)2RMSE = \sqrt{MSE} = \sqrt{{1 \over N} \sum_{i=1}^N(y_i - \hat{y})^2}
  • 로그평균제곱오차 - MSLE (Mean Squared Log/Logarithm Error)

실제값과 추정값에 로그를 씌운 후 오차제곱합 하여 성능을 평가하기 위한 지표로, yi=0y_i=0일 때 마이너스 무한으로 발산하는 것을 막기 위해 +1을 취해 준 형식을 띈다.

MSLE=1N∑i=0N(log⁡(yi+1)−log⁡(yi^+1))2MSLE = {1 \over N} \sum_{i=0}^N(\log (y_i+1) -\log (\hat{y_i}+1))^2
  • 제곱근 로그평균제곱오차 - RMSLE (Root Mean Squared Log Error)

로그평균제곱오차 마찬가지로 제곱을 함으로써 값이 과하게 커지는 특성을 가지므로 이를 줄이고자 root를 씌워 값을 낮춘 평가 지표이다.

RMSLE=1N∑i=0N(log⁡(yi+1)−log⁡(yi^+1))2RMSLE = \sqrt{{1 \over N} \sum_{i=0}^N(\log (y_i+1) -\log (\hat{y_i}+1))^2}
  • R-스퀘어 - R2R^2 (R-Square)

통계학 기법인 분산 분석(ANOVA) 기반으로 예측 성능을 평가하기 위한 지표이며, 0과 1사이의 값을 가지고 1에 가까울 수록 예측 정확도가 높다고 하나 데이터의 선형관계 여부에 관계없이 설명변수의 개수가 많으면 증가 하기 때문에 분석에 유의미한 영향을 줄 수 있다고 오인할 수 있다는 단점을 지닌다. 아래 수식의 용어들이 이해가 안 간다면 여기를 참조하길 바란다.

SSRSST=1−SSESST=R2{SSR \over SST} = 1 - {SSE \over SST} = R^2

그럼 RMSE와 RMSLE간에 무슨 차이가 있냐?

RMSLE는 log를 통해 값을 낮춤으로써 outlier에 강하다는 특성을 지니고, 이 외에도 로그 공식을 통한 상대적 비율을 구할 수 있다는 것, 예측값이 실제값보다 작게 추정된 과소평가된 것에 큰 패널티를 부여한다는 장점이 있다.

Gradient Descent: One of key points in ML

분류와 회귀에 관한 지난 포스트들에서 언급하였지만 구체적으로 다루지 않은 개념이 있다면 대표적으로 머신러닝과 딥러닝의 키포인트 중 하나라고 할 수 있는 경사하강법, 영어로는 gradient descent algorithm이다. 기계학습의 근간이 되는 최적의 학습 알고리즘의 하나로, 지금까지 다룬 분류와 회귀를 넘어 non-linear한 테스크를 다루는데에도 사용된다.

경사 하강 알고리즘의 원리를 간단히 비유하면 이러하다.

산을 넘다가 길을 잃었고 골짜기까지 내려가야 하는데 어느덧 해가 저물고 있어 서둘러야 한다. 이 때 가장 빨리 내려갈 수 있는 방법은 골짜기 쪽으로 제일 경사가 가파른 지점을 통과하는 것이며 안전은 무시하고 가파른 곳들만 통과하다보면 완만한 구간들만 통과하는 것보다 더 빠르게 골짜기에 도착할 수 있을 것이다.

이러한 이유로 경사하강법은 steepest descent algorithm이라고도 불리는데, 함수에서의 설명변수인 독립 변수 값을 변형시켜가면서 궁극적으로 함수의 값인 종속변수가 최소가 되도록 하는 독립 변수 값을 찾는 방법이다. 단순히 함수의 값을 최소/최대화 하는 것이면 미분했을 때의 값이 0이면 되지 않겠냐 생각할 수 있다.

그러나 계산하는 함수가 비선형함수이거나 열린 형태(opened form)이면 오히려 미분계수와 해를 구하기 어렵고, 미분 계수 구하는 과정보다 gradient descent 알고리즘을 컴퓨터에 직접 적용하는 것이 연산이 더 빠르기 때문에 함수의 최솟값이 아닌, 최소로 하는 독립변수의 값을 찾는데에 그 의의를 둔다.

정리하자면 경사하강법은 함수의 기울기(원래 slope지만 여기서는 gradient도 해당한다고 하자)를 이용해 종속변수 xx를 어디로 옮겼을 때 함수값 yy가 최소가 되는지 알아보는 방법이다. 기울기가 양수이면 xx값이 커질 수록 yy값도 커지고, 음수이면 xx가 커짐에 따라 yy는 작아진다.

선형 회귀를 예로 들어보자. 위에서 언급한 것처럼 회귀식은 y=Σwx+by= \Sigma wx+b와 같이 수립할 수 있고, 오차제곱합에 평균을 취한 MSE가 회귀 성능 평가 지표이자 cost function, 우리말로 최적의 회귀식을 구하기 위한 '비용함수' 가 된다.

머신의 관점에서는 이 비용함수를 최소화하는 w와 b를 찾아야 하는데, 평균제곱오차의 공식에 따라 비용함수는 2차원의 포물선 함수형태를 띄어 다음과 같이 표현된다.

linreg_costfunc

IMG Source from bskvision's blog

위 포물선 그림은 각각 w와 b에 대한 이차함수이며, 이 각각의 그림에서 값이 최소가 되는 지점을 찾아야 하는 것이 목적인데 이는 그림에서의 골짜기이며, 수학적으로 미분했을 때 0인 지점이다. 기계는 학습을 할 때 아래 그림과 같이 초기 w(b)값을 임의로 잡고 최솟값을 서서히 찾아간다.(아래 그림은 기울기가 음수일 때의 예시)

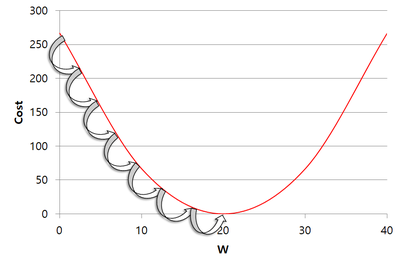
initial_pointcurve and arrow

IMG Source from bskvision's blog, Avengineers's blog

이를 수학적으로 표기하면 cost function을 w에 대한 편미분값에 '학습률(learning rate)'이라는 파라미터 α\alpha(또는 η\eta로 표기)를 곱한 것을 초깃값 w에 빼준 것이며, 공식으로 나타내면 다음과 같다.
다음 포인트 = 현재포인트 - 이동거리 x 기울기의 부호

Wt+1=Wt−η∇E(W)∇Wt∇E(W)∇Wt=(∂E∂w1,∂E∂w2,…,∂E∂wM)W^{t+1} = W^t - \eta{\nabla E(W) \over \nabla W^t} \\ \\ {\nabla E(W) \over \nabla W^t} = ({\partial E \over \partial \bold w_1},{\partial E \over \partial \bold w_2}, \dots,{\partial E \over \partial \bold w_M})

이렇게 반복해서 조정해주면 최소의 값을 찾게 되고, 학습률은 얼마나 빠르게 내려갈 것인지에 대한 스텝 사이즈를 결정한다. 학습률의 영향력을 그림으로 나타내면 이러하다.
difference learningRate

IMG Source from Avengineers's blog

좀 더 동적으로 조정되는 것을 살펴보자. 두번째 움짤에서의 첫번째는 linear regression에서의 GD 알고리즘에 해당된다.
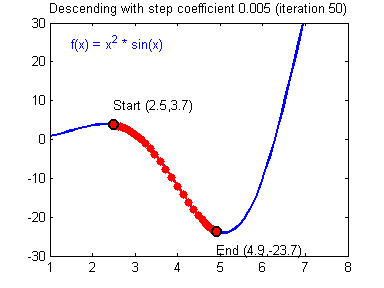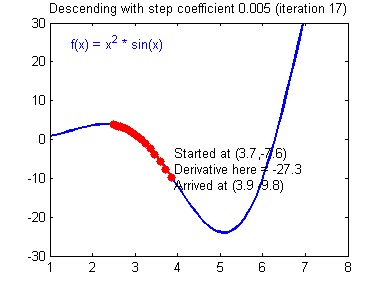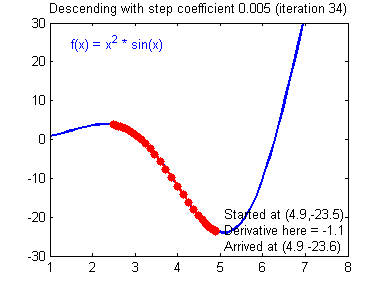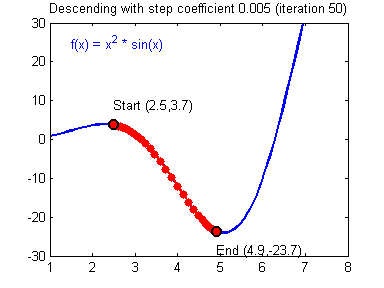
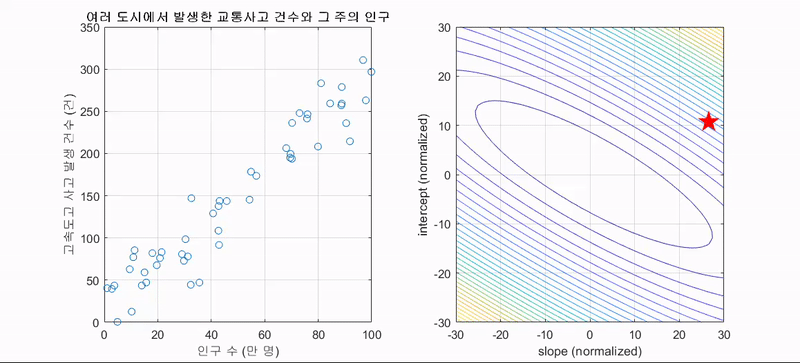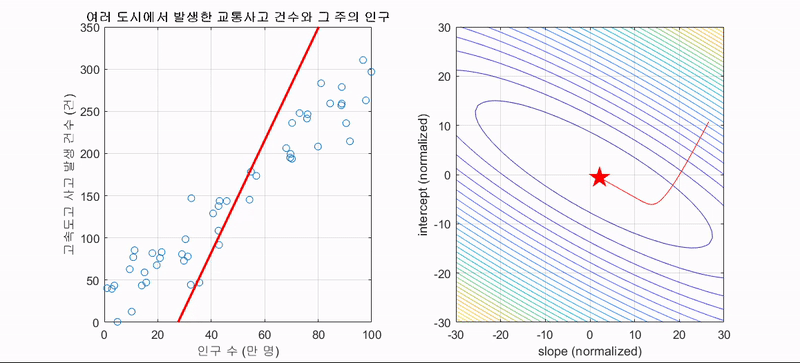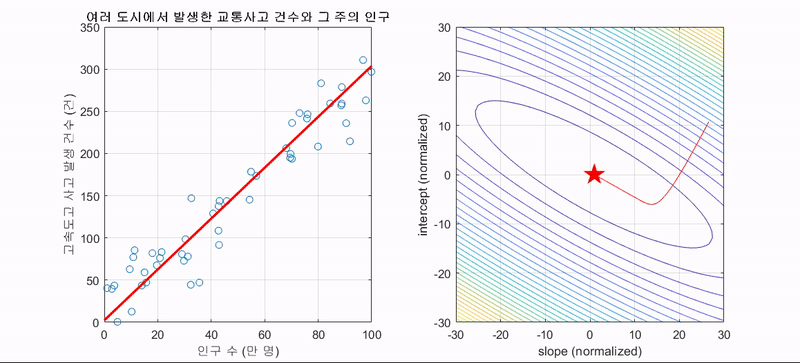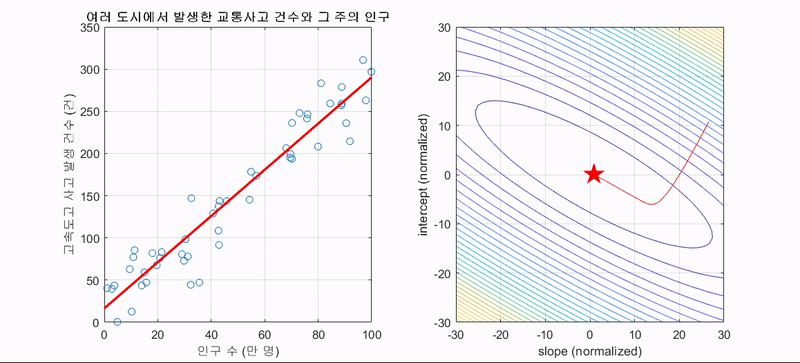
movingGDregressionGD

IMG Source from Angeloyeo's blog

위 예시들은 경사하강법이 머신러닝에서 얼마나 강력한 힘을 발휘하는 알고리즘인지를 잘 표현해주고 있다. 경사하강법은 모든 차원과 모든 공간, 심지어 무한 차원상에서의 적용이 가능하다는 장점을 갖는다. 그러나 단점이라고는 있을까 싶은 이 알고리즘도 명확한 단점이 있는데 정확성을 위해 극값으로 이동함에 있어 많은 수정 단계들을 거쳐야 하고 2차원이 아닌 다차원의 문제를 풀려고 할 때 다음과 같은 문제가 발생할 수 있다.
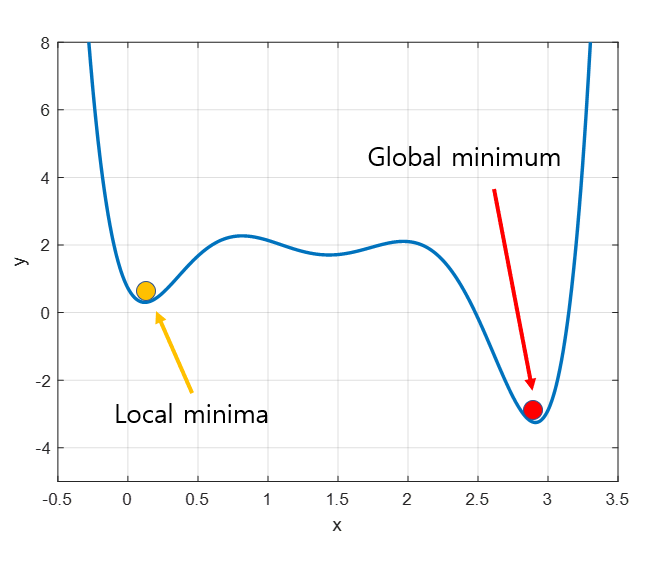
local minima

IMG Source from Angeloyeo's blog

경사하강법이 시작하는 위치는 매번 다르기 때문에 다음과 같이 골짜기가 두 개 이상일 때 실제로는 더 작은 최솟값이 있음에도, 다른 골짜기에 빠져버리는 문제를 담게 된다. 이를 local minima 또는 local minimal이라 하며, 이 local minima 문제를 해결 하기 위한 여러가지 시도들이 현재도 머신러닝 대가들 사이에서 이루어지고 있다.

경사 하강의 종류

지금까지 언급한 경사하강 알고리즘은 full batch라고 하여, 학습데이터를 전부다 읽고 나서 스텝을 밟아나가는 것이다. 머신러닝을 하다보면 학습 데이터가 정말 많아 이를 다 넣고 경사하강법을 시행하기에는 아무래도 효용과 비용을 무시 못하는데, 보통 학습데이터의 일부를 취해 gradient를 구하는 Stochastic Gradient Descent(줄여서 SGD) 기법을 많이 사용한다.
SGD

IMG Source from imgur.com

이런 SGD 기법 외에도 Momentum, RMSProp, Adam 등 다양한 방식이 지금까지 제시 되었고, 딥러닝에서 경사하강법이 많이 사용되는데 아래 도식과 같은 다양한 기법들을 python에서는 가져다 쓸 수 있고, Adam이 주로 많이 사용된다[보물찾기 블로그 포스트, 2017 인용]
kindsOfGD

IMG Source from imgur.com

References

profile
재로미
정확하고 체계적인 지식을 가진 개발자 뿐만 아니라, 가진 지식을 사람들과 함께 나눌 수 있는 계발자가 되고 싶습니다
이전 포스트

[ML] 6편 - Linear tasks : Logistic Regression

post-custom-banner

0개의 댓글