데브코스 48일차 - 머신러닝(SVM, Decision Tree, 비지도 학습)

키워드

SVM, Decision Tree, 비지도학습

SVM

SVM (선형 이론)

• 각 클래스의 데이터 샘플로부터 거리(마진)가 가장 멀리 위치해있다 → 일반화 성능이 좋다

• 마진을 구성하는 데이터 포인트를 서포트 벡터 라고 함

• SVM의 경우 마진을 최대화하는 최적 직선(최대 마진 초평면)을 만드는 것이 목적임

• 최적화 문제

  • 평행한 두 직선 위에 서포트 벡터가 존재
  • 서포트 벡터에 대해 |w^Tx+b|
  • 마진 = 2/||w||

• 최적화 문제 2

  • 마진을 키우면서 모든 데이터를 알맞게 분류

• SVM 종류

  • 하드 마진 svm
    • 어떠한 오분류도 허용하지 않고 완벽한 선형 모델로 분리가 가능
  • 소프트 마진 svm
    • 데이터가 섞인 경우 완벽한 선형 분리가 불가능함
    • 어느정도의 오분류를 허용하면서 오차 발생에 따른 패널티를 비용함수에 부과
    • 하드마진 svm 최적화 과정에 규제 패널티를 도입해 일반화 성능을 올림

• 슬랙 변수

  • 소프트 마진 svm에서 사용하는 개념. 각 데이터 포인트 당 하나의 슬랙변수가 할당
  • 마진을 얼마나 위반하는지를 수치적으로 나타냄
  • 슬랙변수를 최소화하고자 함 → 규제로 사용, 규제의 정도를 정해주기 위해 c라는 하이퍼 파라미터를 사용
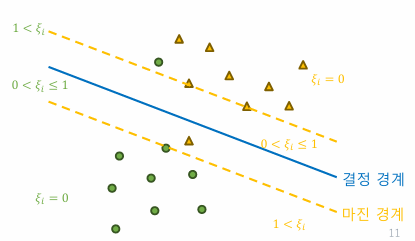
  • 마진을 위반하지 않은 데이터, 슬랙변수=0
    • 서포트 벡터, 서포트벡터보다 멀리있는 데이터
  • 마진을 위반한 데이터
    • 마진 경계~결정 경계: 0<슬랙변수<1
    • 결정 경계 이후: 1<슬랙변수 → 올바르지 못한 클래스로 분류됨
  • 1-슬랙변수: 결정 경계에서 슬랙변수만큼 벗어날 수 있음을 허용하는 과정

선형 실습

SVC(kernel='linear', C=0.1)

• C의 값이 크면 경계를 위반하는 것을 허용하지 않는 것이고, C값이 작으면 어느정도의 위반을 허용하는 것이다.
• C에 따라서 슬랙 변수 크기도 달라짐
• C가 커지면 경계를 위반한 것에 대해 강한 패널티 적용, 결정 경계와 마진 경계 사이 거리가 좁아짐

SVM (비선형)

• 데이터의 복잡성으로 인해 선형 결정 경계로 데이터를 분류할 수 없는 경우가 많음

• 저차원에서 선형으로 나뉘지 않는 데이터를 고차원으로 변형하면 초평면으로 분리할 수 있음

  

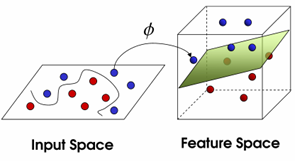
  • 차원이 증가하면 데이터 포인트 간의 상대 거리는 증가
  • 하지만 계산량이 늘어난다는 단점이 있음
  • 이를 해결하기 위해 커널 트릭이 제시됨 → 높은 차원의 장점을 취하면서도 계산의 복잡성이 증가되지 않는 기법

• 커널 트릭

  • 데이터 포인트 사이 내적 계산이 수행되어야 함 → 계산량이 매우 많이 소모됨(고차원 벡터)
  • 이때, 고차원의 내적 연산 결과와 똑같은 결과를 보여주는 저차원 벡터끼리의 연산 함수가 있다면? → 이게 ‘커널’
  • 비선형 SVM에서 많이 사용하는 커널 함수
    • 다항 커널: 다항식으로 보냈을 때의 효과를 누리게 함
    • RBF 커널 (가우시안 커널): 데이터 간 거리에 초점을 맞춘 커널, 일반적으로 많이 사용됨
    • 시그모이드 커널: 이진 분류에 최적화

SVR (Support Vector Regression)

• 회귀 문제로 확장한 SVM 방법
• 주어진 데이터에서 가능한 많은 데이터 포인트를 포함하는 마진 구역(엡실론(허용 오차) 내부의 구역)을 설정

  • 그 구역안에서 회귀 곡선(혹은 초평면)을 찾는 걸 목표로 함

    

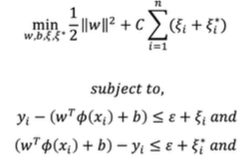
Decision Tree

• 데이터를 나누기 위한 조건은 다양함. 어떤 조건을 선택하냐에 따라 분류 속도가 달라질 수 있음

용어

• 노드: 데이터에 대한 특정 질문이나 조건. 데이터 분류 과정에서 사용
  • 루트 노드: 트리 가장 상단에 위치한 노드
  • 분할 노드(=결정 노드): 데이터를 더 작은 하위 집합으로 나누는 데 사용되는 중간 노드
  • 리프 노드(=터미널 노드): 트리 말단에 위치한 노드. 자식 노드가 없음
• 엣지: 노드와 노드 연결 선

분류 Decision tree

• 데이터 분할하는 기준을 결정하는 데 사용되는 방법론

• 엔트로피: 어떤 상황이나 현상이 품고있는 불확실성 (포함하는 정보량과 반비례)

  

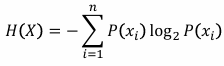
  • 불확실성이 높은 상황일수록, 다양한 사건의 발생 확률이 균일
  • 결정 트리 관점에서 본다면, 각 노드에 포함되는 데이터의 순도(클래스)에 따라 엔트로피가 계산될 수 있음
  • 순도가 높아지도록(엔트로피가 낮아지도록) 트리 구성
  • 부모 노드와 자식 노드들의 엔트로피를 계산해, 엔트로피가 낮아지는 방향으로 결정 경계를 선정! → 정보 이득 (최대화)

• 지니 불순도: 데이터의 클래스 분포의 불균형을 평가하는 방법 (순도를 측정하는 또다른 방법)

  • 0~1의 값을 가짐 → 0: 순도가 높은 상태

    

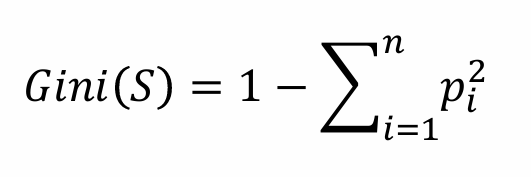
  • 즉 하나의 클래스로만 구성되어있다면(순도가 높다면) p^2의 sum이 1이 되어 지니 불순도가 0이 됨(불균형이 없다는 것을 의미 → 순도가 높음을 의미)

  • 마찬가지로 순도가 높아지도록(지니 불순도가 낮아지도록) 트리를 구성

DecisionTreeClassifier(criterion='entropy', # 'entropy', 'gini'
											 max_depth=3, # 최대 깊이
											 min_sample_split=3) # 데이터 분류를 위한 최소 데이터 수

회귀 Decision tree

• MSE 최소화 방식

  • 각 노드에서 실제 정답과 예측값 사이의 평균 제곱 오차(mse)의 평균을 계산하고 이 값을 최소화하는 노드를 찾아가는 방식으로 트리가 만들어짐

  • 특정 포인트(x)에서 데이터를 두 그룹으로 나누고 각각에서 mse가 최소가 되는 선(x 평행)을 그음 → 각 그룹을 또 두 그룹으로 나눔 → 반복…

    

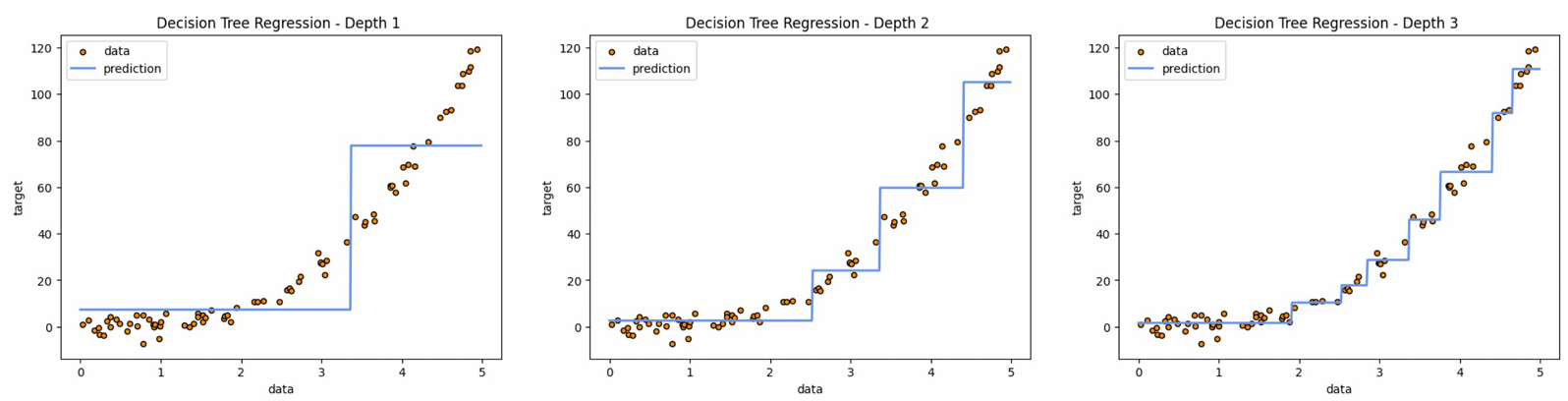
  • max depth가 너무 크면 각 데이터에 너무 맞춰져서 오버피팅 되는 선을 그을것

• 장점

  • 해석 용이성
  • 스케일링에 둔감함

• 단점

  

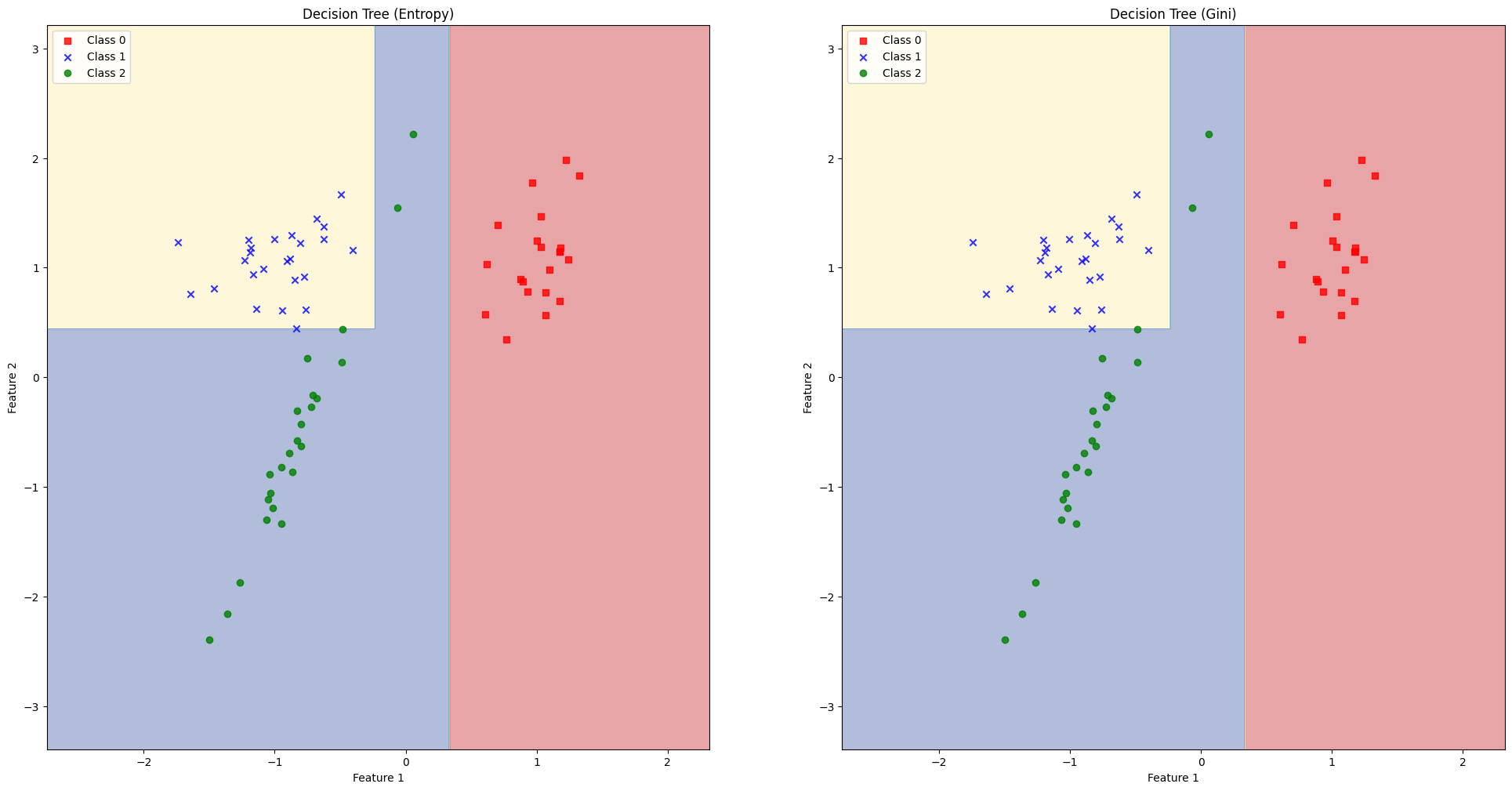
  • 축에 수직인 방향으로 데이터가 분할됨 → 모서리 부분에서 오버피팅이 나타나 일반화가 어려울 수 있음
    • 필요시 주성분 분석을 통한 데이터 회전이 필요할 수 있음
  • 노이즈에 굉장히 민감 (결정 경계면 지정에 영향을 줄 수 있음)
  • depth가 깊다면 강한 오버피팅의 위험이 큼

• 여러개의 tree를 만들어서 다수결 결정을 할 수도 있음 → random forest

실습

SVM 학습 시간은 선형 모델에 비해 오래 걸림

Decision Tree는 SVM에 비해 짧음

• 성능 평가 지표
  • 정확도 (accuracy)
    • 전체 중 얼마나 정답을 맞췄는지 (TP+TN/all)
  • 정밀도 (precision)
    • 예측한 양성 결과 중 실제로 얼마나 진짜 양성인지 (TP / TP+FP)
    • ex) 스팸 메일 중 100% 스팸 메일만 분류해내는 게 중요
  • 재현율 (recall)
    • 실제 양성 중 얼마나 양성을 찾아냈는지 (TP / TP+FN)
    • ex) 암의 경우, 100% 암이 아니더라도 골라내는 게 중요
  • 정밀도와 재현율은 trade-off 관계에 있음
  • f1 score
    • 재현율과 정밀도의 조화 평균
    • 둘 다 적당히 좋은 값을 가져야 높은 f1 score를 가질 수 있음
• learning curve
  • 모델의 크기가 커지고 복잡도가 증가하면 모델의 성능은 올라감
  • 하지만 과적합이 발생하면 오히려 성능 하락 → 학습 데이터에 대한 성능은 지속적으로 상승하지만, 평가 데이터에 대한 성능이 하락
  • 평가 데이터에 대한 성능이 낮아지기 시작하는 지점의 세팅을 이용해 모델을 최적화해야함
• Decision Tree에서 max_depth를 변경해 실험해보며 러닝 커브를 그려보고 적합한 max_depth를 찾음 → 더 높은 성능을 보임
• SVM도 C 상수값을 변경해보거나, 커널을 변경해봄으로써 최적화해볼 수 있음

비지도학습

비지도 학습 (un-supervised learning)

• 정답 레이블이 지정되지 않은 데이터로부터 패턴을 찾아내는 학습 방법론

• 라벨링 할 필요가 없어 비용과 시간이 절약

• 데이터 내부의 구조를 탐색하기때문에 다양한 통찰이 도출될 수 있음

• but, 결과를 해석하기 어려울 수 있음

• 명확한 정답이 없어 모델의 성능 객관화와 평가가 어려움

• 노이즈에 매우 민감함

• 군집화 (Clustering)

  • 데이터를 유사한 특성(내재된 구조)을 가진 하위 그룹으로 분할
  • 군집화 한 데이터의 의미는 사람이 부여해야함!! → 전문가가 투입돼야함

• 차원 축소 (Dimensionality Reduction)

  • 고차원 데이터를 핵심적인 특성을 유지하면서 특성(컬럼)을 줄여 더 낮은 차원의 표현으로 만드는 과정
  • 데이터 시각화, 노이즈 감소, 데이터 해석 등을 목적으로 함

• 이상 탐지

  • 데이터에서 비정상적인 패턴, 예외적 사례를 탐지
  • 일반적인 특성에서 많이 벗어난 데이터를 식별하는 과정에 사용 → 보안, 금융, 의료 분야에서 중요한 역할

비지도학습 대표 알고리즘

• 군집화
  • K-means
    • 데이터를 K개의 클러스터로 그룹화 → 각 클러스터의 중심을 계산하고 각 데이터 포인트를 가장 가까운 클러스터 중심에 할당 (반복을 통해 중심을 업데이트하며 최적화)
  • 계층적 군집화
    • 데이터 포인트를 개별 클러스터로 가정해 시작 → 점차 병합, 세분화
  • DBSCAN
    • 데이터가 모여있는 밀도를 기반으로 클러스터 형성. 너무 저밀도면 이상치로 분류
• 차원 축소
  • 주성분 분석 (PCA)
    • 데이터의 분산을 최대한 보존하는 방향의 축을 찾아 해당 축을 기준으로 고차원 데이터를 저차원으로 변환
  • t-SNE
    • 고차원 데이터의 구조적 특성을 보존하면서 저차원으로 매핑
    • 이를 이용해 시각화를 많이 함
  • 오토 인코더 (Autoencoder: encoder+decoder)
    • 딥러닝을 이용한 차원 축소 기법 → 입력 데이터를 저차원으로 압축 후 다시 원래 차원으로 복원하는 방식으로 핵심 특징을 만들어냄
• 이상 탐지
  • Isolation Forest
    • tree를 기반으로 특정 데이터 포인트를 격리시키는 데 필요한 분할 수를 기준으로 이상치를 탐지 (떨어져있는 데이터의 경우 분할수가 작음)
  • One-class SVM
    • 정상 데이터만을 이용해 SVM을 학습 → 이상치를 받으면 output 점수가 낮음 → 이상치 탐지
  • LOF (Local Outlier Factor)
    • 주어진 데이터 주변의 데이터 밀도를 계산 (밀도가 낮으면 이상치!)