데브코스 49일차 - 머신러닝(K-means Clustering, Isolation Forest)

키워드

k-means clustering

K-means Clustering

• K-평균 군집화

  • 전체 데이터를 K개의 덩어리(클러스터)로 나누는 비지도 학습법
  • 각 클러스터의 좌표 값의 평균으로 중심을 정할 수 있음

• 로이드 알고리즘 vs 엘칸 알고리즘(거리 계산시 삼각 부등식 사용)

• 순서

  • 초기화
    • K개의 클러스터 중심점(최종 결과에 큰 영향을 미칠 수 있음)을 임의로 선택
    • 각 중심점이 최대한 멀어질 수 있도록 k-means++ 초기화 방법을 많이 사용
  • 할당
    • 각 데이터 포인트를 각 클러스터 중심과 (유클리드) 거리를 계산해 가장 가까운 중심의 클러스터에 할당됨
  • 업데이트
    • 각 클러스터의 데이터 평균 위치로 중심의 위치를 업데이트
  • 반복
    • 다시 클러스터 중심과 각 데이터 포인트들과의 거리를 계산해 클러스터 재할당
    • 중심의 위치 변화가 없거나, 클러스터 변화가 없거나, 지정된 횟수에 도달할 때까지 반복

• 엘보우 메소드

  • 적절한 K를 고르는 방법. 적절한 K를 선택해야 데이터가 잘 나뉘게 됨
  • 클러스터 수를 늘려가며 각각에 대한 클러스터링 성능을 측정
  • 클러스터의 성능은 SSE(Sum of Squared Errors-각 클러스터 내의 데이터포인트와 클러스터 중심간의 거리의 제곱합) 값을 활용
    • 무조건 SSE가 낮다고 좋은 게 아님 → SSE의 감소율이 급격히 줄어드는 지점을 최적 클러스터 수(K)로 간주
  • 직접 보고 골라야함

• 실루엣 계수 (보조적인 평가 방법)

  • 클러스터 안의 응집도와 서로 다른 클러스터 간의 분리도를 고려해 군집화의 품질을 평가하는 방법
  • 응집도(↓, a(i)): 특정 데이터에 대해 동일한 클러스터 안에 들어있는 다른 데이터들과의 평균 거리
  • 분리도(↑, b(i)): 특정 데이터에 대해 다른 클러스터 중 가장 가까운 클러스터의 중심까지의 거리
  • s(i) = b(i) - a(i) / max(a(i), b(i))
    • 최대값 1 → a(i)가 거의 0에 근접해 b(i)만 남는 상황 → 좋은 상황
    • 최소값 -1 → b(i)가 작아지고 오히려 a(i)가 커지는 경우 → 나쁜 상황

실습

• 데이터: mall customer data: 200명의 쇼핑몰 고객에 대한 정보 데이터

  • 나이, 연간 소득, 쇼핑 점수와 같은 수치형 데이터는 스케일 매칭해줘야 함 → 이는 거리 기반 군집화에서 중요한 요소임

• 문제: 주어진 고객 데이터를 바탕으로 고객을 세분화, 군집화

  • 즉 나이, 성별, 소득, 쇼핑 점수 등이 입력으로 들어오면 몇 번 클러스터인지 분류해냄

• 전처리

  • 성별 (카테고리 데이터) 원핫 인코딩
  • 수치형 데이터 스케일링 (standard scale)

• K 값을 찾으려면 sse, 실루엣 계수를 살펴보고 결정

  • 실루엣 계수 간 차이가 크지 않다면 작은 K를 기준으로 하는 게 좋은 선택

• sse, 실루엣 계수들을 이용해 결과를 평가하는 것도 좋지만, 결국은 데이터를 그려보고 해석해야함

• t-sne를 이용해 4차원 데이터를 2차원으로 변환

• kmeans.labels_ 로 각 데이터에 클래스 번호를 붙인 데이터를 볼 수 있음

• 이 데이터의 기술 통계를 확인해 각 클러스터의 특징을 살펴본다.

  • 만들어진 클러스터가 어떤 의미가 있는지 도메인 지식을 이용해 추측해야함

이상탐지

• 이상치 판단 및 제거 (전통적인 통계 기반 방법)
  • IQR → 1사분위수(Q1), 3사분위수(Q3)
  • 계산이 복잡하지 않고 해석이 직관적임. 하지만 데이터가 대칭이 아니거나 복잡한 분포를 갖고있다면 오인식의 가능성 커짐
• 머신러닝을 활용한 이상탐지
  • 모델로 데이터의 패턴을 익히고 그 패턴에서 벗어난 데이터를 이상치로 취급
  • 복잡한 데이터의 패턴에 적응적
  • but, 모델이 복잡하고 사람이 해석하기 어려울 수 있으며, 양질의 데이터가 다수 필요

Isolation Forest

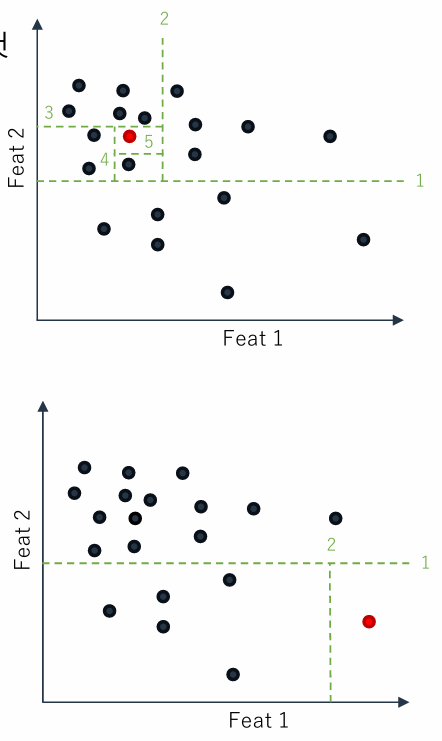
• 정상 데이터는 다른 비슷한 데이터와 밀도있게 모여있을 것. 반면 이상치 데이터는 밀도가 낮은 공간에 존재 → 하나의 데이터를 고립하도록 어떤 특성과 그것의 분할값을 기준으로 나눔

  • like Decision Tree..

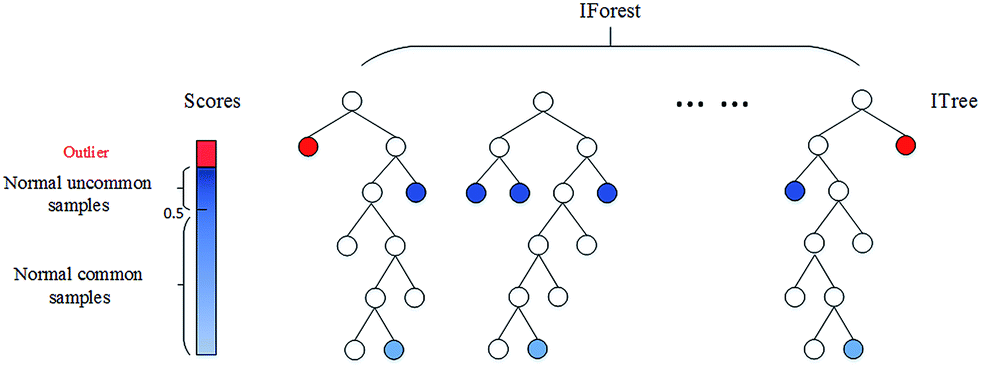
  • 이상치 데이터는 낮은 수준(depth)의 분할 과정으로도 쉽게 고립시킬 수 있다.

    

    

• 과정

  • 데이터 준비
    • 전체에서 무작위로 서브 데이터셋 선택 (하나의 데이터가 여러 서브 데이터셋에 포함될 수 있음)
  • 트리 생성
    • 하나의 서브 데이터셋마다 개별 Isolation Tree(ITree)를 준비
  • 고립 시작
    • 각 트리에 소속된 데이터셋을 하나씩 고립
    • 임의의 특성과 임의의 특성 분할값을 선택. 데이터셋이 리프 노드에 도달할 때까지 반복
    • 각 데이터포인트는 리프노드까지 도달한 깊이를 저장하고있음
  • 고립 완료
    • 하나의 트리에 소속된 모든 데이터셋을 전부 고립
  • 이상치 점수 계산
    • 평균 깊이를 바탕으로 특정 함수를 통해 각 데이터 포인트의 이상치 점수를 계산
  • 이상치 추출
    • 이상치 점수와 특정 임계값을 비교해 이상치 추출

n_estimators = 고립 트리의 수(=서브 데이터셋 수, 이 값이 클수록 안정성과 정확성 향상 but 메모리 사용량도 증가)
max_samples = 서브 데이터셋에 포함될 최대 데이터 포인트의 수
contamination = 전체 데이터셋에서 이상치 데이터가 차지할 비율 (모른다면 'auto'로 설정)

• 평가
  • 이상치 데이터 정답을 알고 있다면, 이상 데이터를 양성으로 놓고 분류 형태의 문제로 평가 가능
  • 정확도, 재현율, 정밀도, f1 score 등을 이용
  • 정답이 없다면, 시각화를 통한 전문가 검토 진행

실습

• credit card fraud detection 데이터

• 입력: 거래 관련 데이터(time, amount, v1~v28) 출력: 이상치 여부

• time(시계열 데이터)의 경우 주기성을 갖고있음 → 주기함수를 적용하는 것도 좋은 방법이지만, 여기선 추가적인 정보가 부족.

  • 큰 outlier가 없어보이므로 min-max scaler을 사용

• amount는 치우침이 있지만 의미가 있기 때문에 log 스케일링 진행

• V 데이터는 pca를 통해 차원 축소된 데이터기 때문에 어떤 의미를 갖는 데이터인지는 알 수 없음

• confusion matrix를 통해 결과 확인. TP 값이 커야 잘 한 분류임

• 쉬운 task는 아니다.. (데이터에서 양성의 비율이 작기 때문에)