Fall 2021 machine learning lecture
관계를 잘 설명하는 직선은 산점도에 있는 점들 대부분이 직선과 가까운 위치에 있는 경우
어떤 점의 경우 직선 위에 놓여있을 정도로 가까운 직선이라면 우리가 찾던 직선일 가능성이 높다. 아쉽게도 모든 점들이 직선 위에 놓일 수는 없기 때문에 우리는 직선이 모든 점에 대해 가장 가깝다고 객관적으로 판단할 수 있는 기준을 삼아야한다. 그 기준을 모든 점에서 떨어진 거리를 측정했을 떄, 평균적으로 가장 가까운 직선으로 생각해 볼 수 있다.
최적선을 찾는다 line of best fit, 데이터에 가장 잘 맞는 가설 함수를 찾아야 함
이런 직선을 찾는 방법을 선형 회귀, Linear regression 이라고 한다.
최적선을 찾아내기 위해 다양한 함수 시도
시도하는 함수 하나하나를 가설 함수 (hypothesis function)이라고 부름
선형 회귀의 임무는 계수 a와 상수 b를 찾아내는 것 y= ax + b
OLS 최소제고법, 예측과 훈련세트에 있는 타깃y 사이의 평균제곱오차를 최소화하는 파라미터를 찾는다.
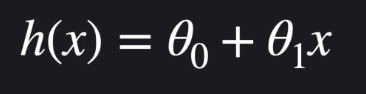
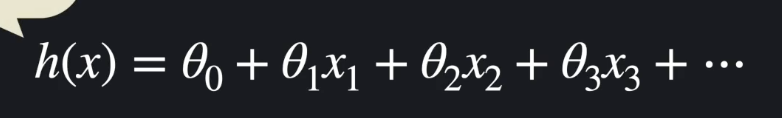
선형 회귀 임무는 가장 적절한 세타 값을 찾아내는 것
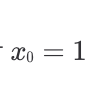
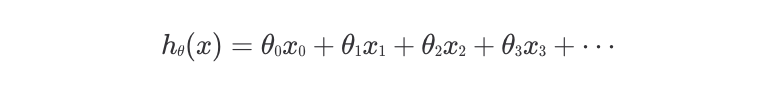
가설함수 h가 세타 값들에 의해 결정된다
Y 종속 변수 = 답 > 지도학습, 회귀
목표 변수 x : 맞추려고 하는 값 target variable / output variable
입력 변수 y : 맞추는데 사용하는 값 input variable / feature
학습 데이터의 개수 : m
단순 선형 회귀 (simple Linear Regression)
1개의 독립변수(x)를 통해 종속변수(Y)를 설명 또는 예측 하는 경우
다중 선형 회귀
1개 이상의 독립변수를 통해 종속변수를 설명 또는 예측하는 경우
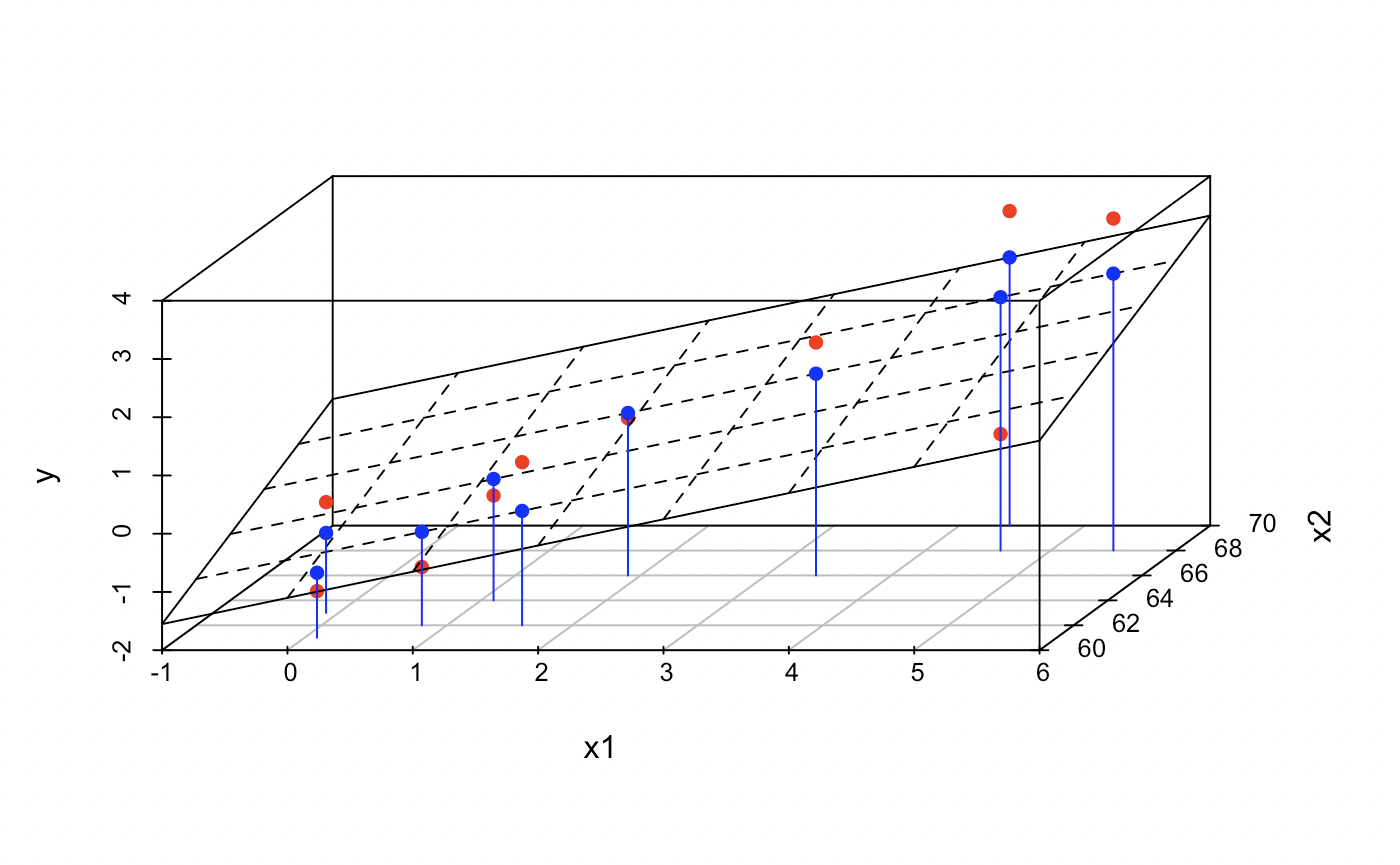
다중 선형 회귀의 경우, 독립 변수가 2개인 경우까지는 3차원 그래픽을 통해 회귀 평면 (regression plane)을 시각적으로 확인할 수 있지만 독립변수가 3개 이상이 되면 시각적으로 확인이 불가능하다.
상상할 수 없지만 4차원 이상 고차원에서의 평면을 초평면(hyper plane)이라고 한다.
모형 = 모델
선형 회귀 모형은
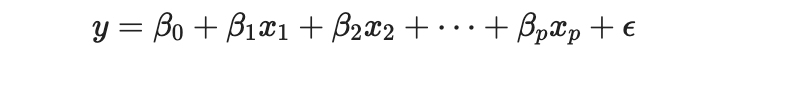
독립변수(X)들은 종속변수(Y)를 설명할 수 있는 변수들로 선택됨
테스트 데이터로 학습하는 과정을 통해 각 독립변수가 종속변수에 어떤 영향을 주는지 설명할 수 있는 beta값을 추정하게 된다. epsilon의 경우 우리가 선택한 독립변수 이외에 종속변수에 영향을 줄 수 있는 노이즈(noise)를 모형에 고려하기 위해 추가된 것
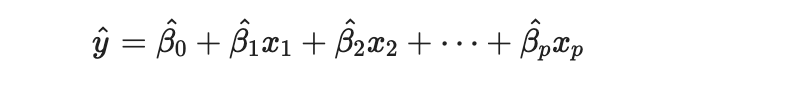
학습으로 beta를 추정해 생성된 모형
성능평가지표 MSE, R^2
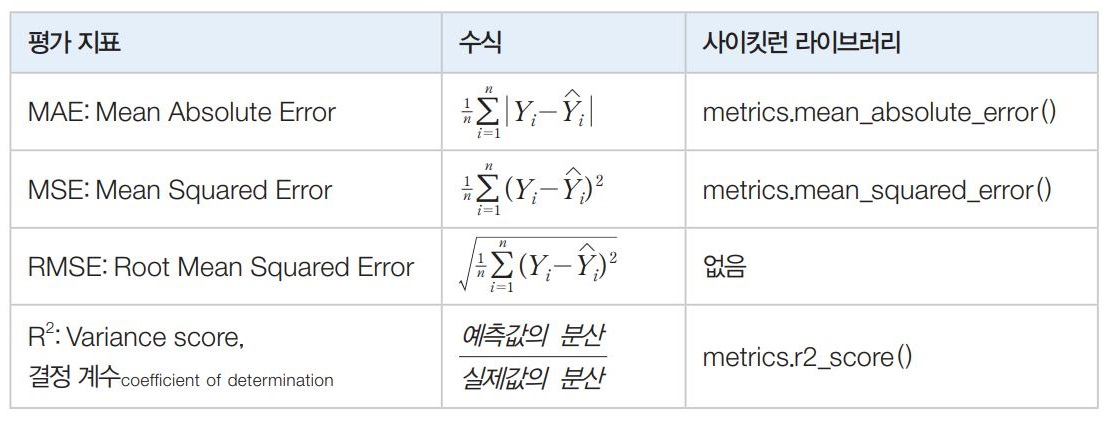
MAE(Mean Absolute Error) : 실제값과 예측값의 차이를 절댓값으로 변환해 평균한 수치
MSE(Mean Sqaured Error) : 실제값과 예측값의 차이를 제곱하여 평균한 수치
RMSE(Root Mean Squared Error) : MSE에 루트(제곱근)을 씌운 수치. 실제 오류 평균보다 더 커지는 특성이 있으므로 이를 방지해준다.
RMSE같은 경우는 직접적으로 제공하지 않아 MSE지표에서 직접 Sqrt()를 씌워주어야 한다.
R2 Score(결정계수) : 분산 기반으로 예측 성능을 평가한다. 실제 값의 분산 대비 예측값의 분산 비율을 지표로 하며, 1에 가까울수록 예측 정확도가 높다.
가설 함수 평가법
평균 제곱 오차 (Mean Squared Error) : 이 데이터들과 가설 함수가 평균적으로 얼마나 떨어져 있는지 나타내기 위한 하나의 방식
오차는 예측 값에서 원래 값을 뺀다. 이 오차값들을 모두 제곱한다. 제곱한 값들을 더한다. 그리고 이것들의 평균을 내기 위해서 총 데이터 개수 만큼 나눈다.
평균 제곱 오차가 크다는 건 가설 함수와 데이터들 간의 오차가 크다는 거고, 결국 그 가설 함수는 데이터들을 잘 표현해 내지 못한 것
- 평균 제곱 오차가 크면 : 가설 함수가 데이터에 잘 안맞다
- 평균 제곱 오차가 작으면 : 가설 함수가 데이터에 잘 맞다
왜 오차의 제곱을 더할까?
- 차이를 계산하며 양수일 때도 있고 음수 일 때도 있기 때문, 양수 5든 음수 -5든 똑같이 취급해야한다.
- 더 큰 오차를 부각시키기 위해서
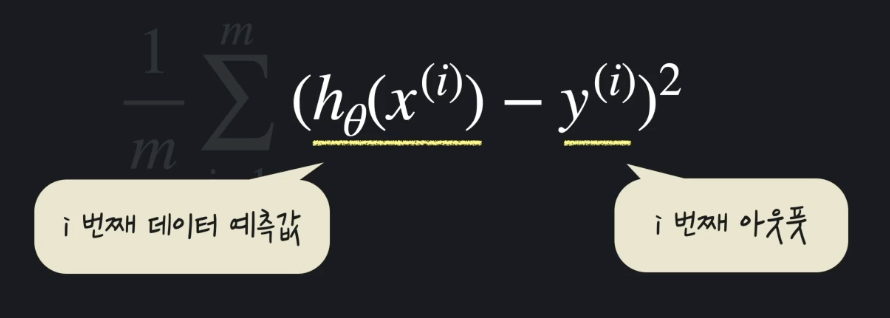
예측값 - 실제 데이터 값 = 오차
가설 함수에서 바꿀 수 있는 것은 세타 값. 세타 값들을 잘 조율해서 가장 적합한 가설 함수를 찾아내는 것.
결국 손실 함수의 아웃풋은 이 세타 값들을 어떻게 설정하느냐에 달려 있는 것.
손실 함수의 인풋이 세타, x와 y는 변수처럼 보이지만 사실 정해진 데이터를 대입하는 것이기 때문에 얘네들이 오히려 변수가 아니라 상수라고 할 수 있다.
손실 함수 (Loss Function) = 비용 함수 (Cost Function)
가설 함수의 성능을 평가하는 함수
손실 함수가 작으면 : 가설 함수가 데이터에 잘 맞다
손실 함수가 크면 : 가설 함수가 데이터에 잘 안 맞다
경사 하강법 (Gradient Descent)
극소점 찾기
학습률 알파가 너무 크면 경사 하강을 한 번 할 때마다 쎄타 값이 많이 바뀜
너무 크면 경사 하강법을 진행할 수록 손실 함수 J의 최소점에서 멀어질 수 있음. 너무 크면 아예 극소점에서 점점 멀어질 수도 있다.
학습률 알파가 너무 작으면 최소 지점을 찾는데 너무 오래 걸림. 극소점까지 너무 오래 걸릴 수 있다.
적절한 학습률, 알파를 적당한 크기로 정하는 게 중요. 빠르고 정확하게 최소점까지 도달하는 학습률이 가장 좋음.
가설 함수 = 모델
sklearn 라이브러리
KNN Regression과 비교하면 직선을 사용한 예측이 더 제약이 많아 보인다. 데이터의 상세 정보를 모두 잃어버린 것처럼 보임. 타깃 y가 특성들의 선형 조합이라는 것은 매우 과한 가정, 하지만 특성이 많은 데이터셋이라면 선형 모델은 매우 훌륭한 성능을 낼 수 있음. 훈련 데이터보다 특성이 더 많은 경우라면 어떤 타깃y도 완벽하게 훈련 세트에 대해서 선형 함수로 모델링할 수 있다.
매개변수가 없는 것이 장점이지만 모델의 복잡도를 제어할 방법이 없다.