Binary Search

Binary Search

이진 검색? 이분 탐색? 이진 탐색? 개념은...

Binary Search

이진 검색 알고리즘(binary search algorithm)은 오름차순으로 정렬된 리스트에서 특정한 값의 위치를 찾는 알고리즘이다. 처음 중간의 값을 임의의 값으로 선택하여, 그 값과 찾고자 하는 값의 크고 작음을 비교하는 방식을 채택하고 있다. 처음 선택한 중앙값이 만약 찾는 값보다 크면 그 값은 새로운 최댓값이 되며, 작으면 그 값은 새로운 최솟값이 된다. 검색 원리상 정렬된 리스트에만 사용할 수 있다는 단점이 있지만, 검색이 반복될 때마다 목표값을 찾을 확률은 두 배가 되므로 속도가 빠르다는 장점이 있다.

고마워요 위키백과!

길이가 N인 정렬된 배열에서 원하는 값의 위치를 찾을 때,

시간 복잡도는 $O(logN)$
증명은 검색만 해도 너무 많이 나와서 생략, 대충 길이가 N인 배열을 반으로 가르고, 가르고 k번 가르면 $N = 2^{k}$ 가 되어서...

구현

주어진 정렬 된 배열에서 원하는 값의 위치를 찾는 기능은
Python의 경우 내장 라이브러리인 bisect 라이브러리로 쉽게 쓸 수 있다. bisect를 뜯어보자.

def bisect_left(a, x, lo=0, hi=None):
    if lo < 0:
        raise ValueError('lo must be non-negative')
    if hi is None:
        hi = len(a)
    while lo < hi:
        mid = (lo+hi)//2
        # Use __lt__ to match the logic in list.sort() and in heapq
        if a[mid] < x: lo = mid+1
        else: hi = mid
    return lo

def bisect_right(a, x, lo=0, hi=None):
    if lo < 0:
        raise ValueError('lo must be non-negative')
    if hi is None:
        hi = len(a)
    while lo < hi:
        mid = (lo+hi)//2
        # Use __lt__ to match the logic in list.sort() and in heapq
        if x < a[mid]: hi = mid
        else: lo = mid+1
    return lo

오름차순으로 정렬 된 배열 a와 목표 값 x를 받으면, 배열에서 정렬을 유지하도록 x가 삽입될 때 그 index 값을 반환한다.

bisect 라이브러리 함수들은 C로 구동되기 때문에, 훨씬 빠르다. 그냥 쓸 수 있으면 쓰자!

그럼 이분탐색을 왜 공부하지?

이분탐색의 핵심 아이디어인 중앙 값 조사 후 구간 재설정으로 효율적으로 풀 수 있는 문제가 많기 때문이라고 본다.

특히 Parametric Search나 분할 정복 문제에도 비슷한 아이디어가 쓰인다.

분할 정복의 경우 mid를 기준으로 주어진 문제를 분할하여 더 작은 구간에 대해서 분할을 반복하여 문제를 푼다. 분할할 때 주로 구간의 중앙값을 활용한다. (반드시 중앙값일 필요는 없다.)

def quick_sort(arr):
    def sort(low, high):
        if high <= low:
            return None

        mid = partition(low, high)
        sort(low, mid - 1)
        sort(mid, high)

    def partition(low, high):
        pivot = arr[(low + high) // 2]
        while low <= high:
            while arr[low] < pivot:
                low += 1
            while arr[high] > pivot:
                high -= 1
            if low <= high:
                arr[low], arr[high] = arr[high], arr[low]
                low, high = low + 1, high - 1

        return low

    return sort(0, len(arr) - 1)


def merge_sort(arr):
    def sort(low,high):
        if high-low <= 1:
            return arr[low:high]

        mid = (low+high)//2
        left_list = sort(low,mid)
        right_list = sort(mid,high)
        return merge(left_list,right_list)

    def merge(left,right):
        result = []
        i = 0
        j = 0
        while i < len(left) or j < len(right) :
            if i < len(left) and j < len(right):
                if left[i] <= right[j]:
                    result.append(left[i])
                    i += 1
                else:
                    result.append(right[j])
                    j += 1
            elif i < len(left):
                result.append(left[i])
                i += 1
            else:
                result.append(right[j])
                j += 1
        return result
    return sort(0,len(arr))

분할정복의 예인 퀵소트와 머지 소트

---

Parametric Search는 결정 문제 (얘보다 더 나은 답이 있나요?)를 최적화 문제 (최적 답이 무엇인가요?)로 바꿀 수 있다.

뭐 주어진 조건에서 가능한 최소값을 구하라거나, 최대 값을 구하라는 문제에서 답의 후보들 중 최소값을 low_bound로, 후보 중 최대값을 upper_bound로 잡고, 이분 탐색을 통해 조건이 만족되는 경계를 찾을 수 있다.

너모 대충 그린 그림...

느낌 아시겠죠? ^~^

예제들
BOJ_랜선 자르기
BOJ_나무 자르기

(다 자르네)

그래서 언제 써야 좋을까?

최적화 문제는 꼭 이분탐색으로만 풀 수 있는 것은 아니다.
경우에 따라 그리디 알고리즘, 동적 프로그래밍, (백트래킹을 끼얹은) 완전탐색이 나을 수도 있다. 어쩔 때는 그냥 문제를 표현하는 수식이 구해져서 그냥 풀리는 경우도 있다.

개인적으론 함수의 개형은 잘 모르겠지만, x에 대해 f(x)를 구하기가 그렇게 어렵지 않은 경우, 점화식이 딱히 없는 경우, 최적 해가 유일한 값임이 자명하고 다변수라면 차원이 독립적일 때, 최적 해를 기준으로 f(x) 값이 확실히 구분될 때 (단조함수일 때) 이분 탐색 접근이 빛을 발한다.

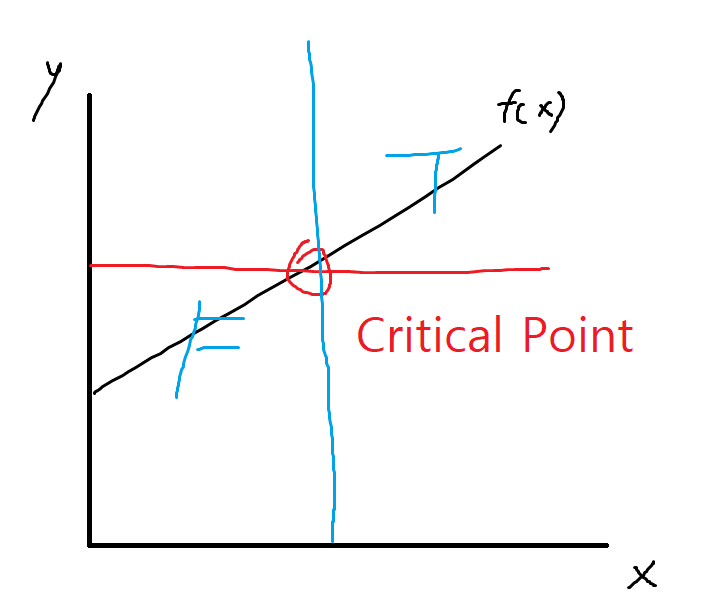
이런 경우... x에 대한 f(x) 값을 구하면서 이분 탐색을 통해 최적 x를 찾아갈 수 있다.

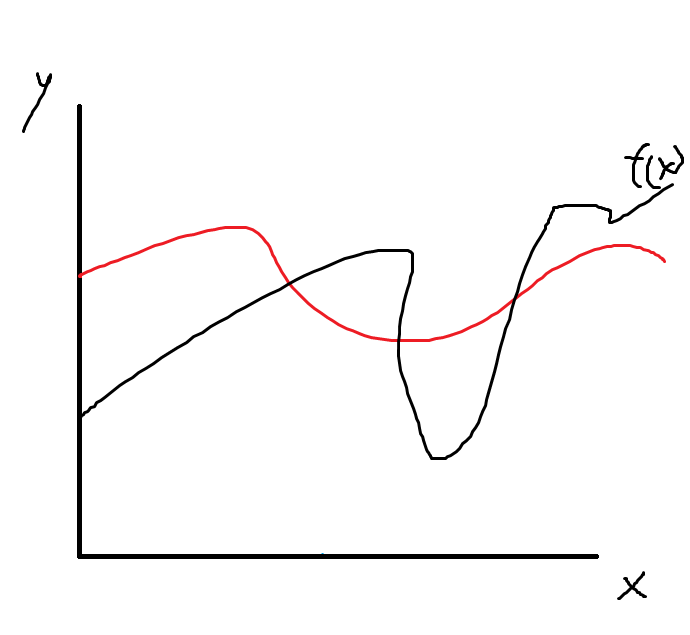
이런 f(x)나 임계 조건을 주고 빨간 선과 만나는 부분들을 찾으라면 이분 탐색은 바보가 되어버린다... ㅜ

(적절한 구간 설정으로 못할 건 없지만, 다른 접근이 더 유용할 가능성이 높다)

그 밖에 의외의 문제도 이분 탐색을 사용해서 접근할 수 있다.

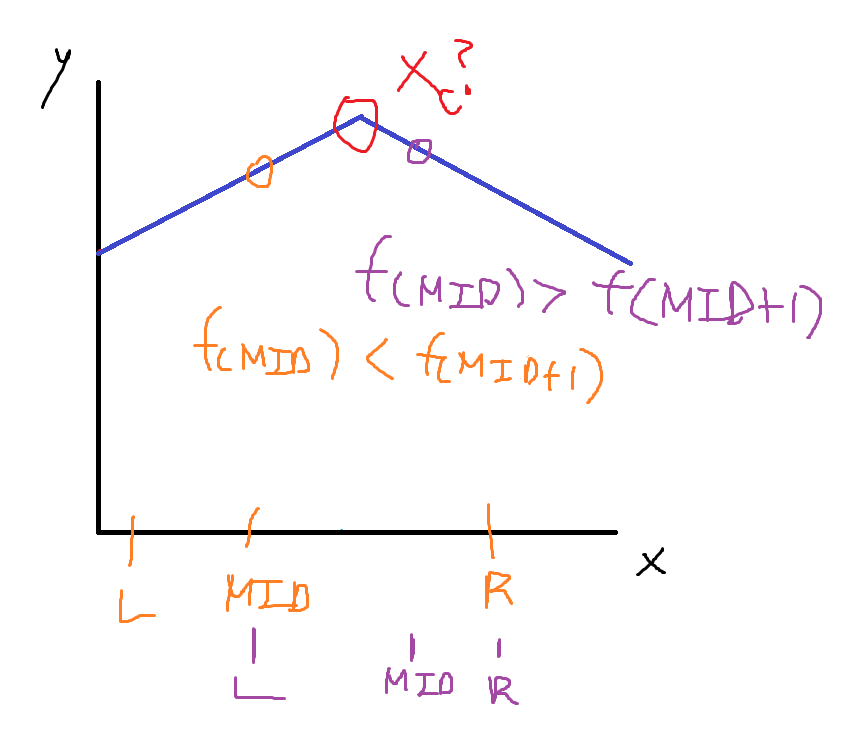
주어진 함수의 극 값을 구하는 문제, 함수의 개형을 안다면 미분을 통해 쉽게 구할 수 있지만 모른다면 다음과 같이 f(x) < f(x+1) 일때를 False, f(x) > f(x+1) 일 때를 True로 보고 이분탐색을 통해 $x_c$를 구할 수 있다.

이 경우 구간을 이분하는 것이 아닌 삼분하는 접근으로도 풀 수 있긴 하다.

알고리즘 문제 풀이 시 이분 탐색의 핵심 아이디어인 구간을 2개로 나누어서 f(mid) 값에 따라 구간을 선택하여 구간을 줄이는 방법은 숙지만 잘 하면 되고, 중요한건 주어진 문제에서 f(x)를 얻는 함수를 구현하는 것과 이분 탐색을 써도 되는지 검증하는 것이 더 중요하다고 생각한다.

---

추천 문제

BOJ_상근타워
유형은 이분탐색인데 안 써도 되는 문제

BOJ_두 수의 합
역시 유형은 이분탐색인데 투 포인트 알고리즘이 더 풀기 편하다.

Programmers_징검 다리
이분 탐색으로 풀긴 했는데 그리디로도 충분히 풀 수 있을 듯 하다.

어째 올리고 보니 이분탐색을 쓰지 말라는 문제만 올린다.

Programmers_금과 은 운반하기
월간 코드 챌린지 시즌3 9월 3번 문제, 이분 탐색은 맞는데, f(x)를 구하는 것이 꽤 골치인 문제. 저는 당시 못 풀었었습니다.

BOJ_뱀파이어 김상근 백작
완전 탐색의 가짓 수를 이분 탐색을 활용하여 줄이자.

---

그 밖에 구현 시 자주 겪는 문제들

이-글이 정리가 잘 되어 있어서 그냥 링크합니다.

left = mid +1 이냐, right = mid -1 이냐, while left < right: 를 했더니 왜 루프가 안끝나니! 할 때 봅시다. (보통은 그냥 생각하기 귀찮아서 테스트 케이스를 왕창 넣는 것과 로깅으로 해결하긴 합니다...)