Prim 알고리즘 (2) 힙과 인접 리스트 사용

Jeuk Oh·2021년 8월 30일

그래프 알고리즘

알고리즘 정리

목록 보기

4/5

개요

이전 포스팅에서 MST를 인접 행렬을 사용하여 구하는 Prim 알고리즘을 공부해보았다.

이전 글을 빌리면,

시간복잡도는 편입될 정점 V개를 정하고, 인접행렬에서 간선의 개수를 검색하는데 V개의 연산이 필요하므로 $O(V^2)$

위키에 따르면, 인접 행렬이 아닌 이진 힙 + 인접 리스트를 사용하면 $O(ElogV)$

오늘은 힙과 인접 리스트를 사용한 Prim 알고리즘을 알아보자.

Prim 알고리즘이란

복습 ~~겸 분량 채우기~~

한 정점에 연결된 간선 중 하나씩 선택하면서 최소 신장 트리를 완성하는 알고리즘

시작 정점을 루트로 하는 그래프 내 트리를 생각하자
시작 정점에 연결 된 간선 중 최소 가중치로 연결된 정점을 트리에 자손으로 편입
트리에 편입된 정점과 비트리 정점과 연결된 모든 간선 가중치를 확인하고 또 다음 비트리 정점을 편입하러 간다.
모든 비트리 정점들은 트리에 인접할 수 있는 최소 가중치를 업데이트 및 저장 (인접 안할 땐 INF 값)
어떤 비트리 정점을 편입시키느냐 -> 트리에 편입하는 비용이 가장 낮은 비트리 정점.
시작 정점을 제외하고 모든 비트리 정점 V-1개에 대해 1개의 간선을 선택하므로 V-1개의 간선이 선택된다.

선택된 트리와 간선이 최소신장트리

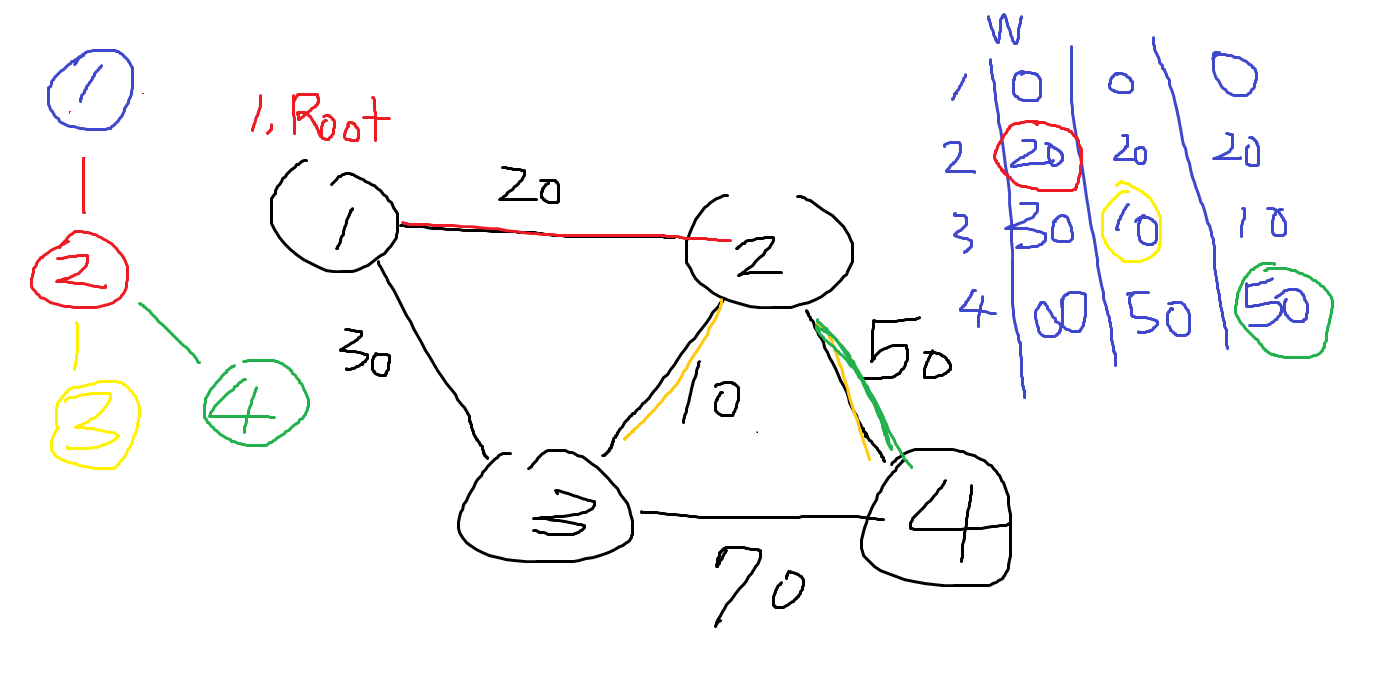
차이점

이전 글을 열심히 복기해보자. Prim 알고리즘의 핵심은

1. 트리에 속하지 않은 정점들 중
2. 트리에 인접한 간선에서
3. 최소 가중치의 간선을 선택

으로 볼 수 있다.

지난 글에서 구현한 인접 행렬을 이용한 Prim 알고리즘은 세 핵심 구조를 다음과 같이 처리한다.

1. visited 리스트를 사용하여 처리
2. 정점이 트리에 편입 될 때마다 정점의 인접 간선 정보를 업데이트
3. 정점 별 최소 비용을 업데이트하여 다음 최소 가중치 간선을 고름 (min_adj)

이 때, 정점 V개에 대해서 편입 정점을 고르고 간선을 업데이트 과정에서 $O(V^2)$ 시간 복잡도가 나타난다.

극단적인 경우에는 E가 V-1개라고 하더라도 같은 시간 복잡도를 가져 좋지 않다.

간선의 개수가 적다면 인접 행렬은 대부분 비어있다. 굳이 V*V 사이즈의 행렬을 가질 필요가 없다 -> 인접 행렬을 인접 리스트로 바꿔주어 시간 복잡도를 줄일 수 있다. V -> E
인접 행렬의 방법을 보면, 최소 가중치 정점을 고르고 최소 간선을 트리와 잇고 인접 간선 정보를 업데이트 하는 것을 반복한다. -> 최소 가중치 정점에 대한 것을 모두 생략하고 트리와 인접한 간선의 정보 중 최저 간선만 쓰면 된다.

이 때 트리와 인접한 간선들 중 최소 간선만 빠르게 얻기 위해 힙 구조를 사용한다.

힙에 대한 것은 다음에... 배열 전체를 정렬하진 않고 배열의 최소, 최대 값을 이진트리 구조로 빠르게 얻어낼 수 있어 배열의 모든 값에 접근할 필요가 없을 때 편하다.

구현

#인접 리스트를 편리하게 사용하기 위한 defaultdict와
from collections import defaultdict
# 힙 구조 사용을 위한 heapq import
from heapq import *

#인접 리스트 저장용
adj = defaultdict(list)
#인접 리스트는 adj[V1] = [[weight,V2],..] 
#형식으로 저장되어있다.
...

# 트리의 노드들 저장 (vistied와 같은 역할)
Tree_node = set([0])
# 트리에 인접한 간선을 저장하는 cand_list
# 첫 간선으로 0번째 노드의 간선을 몽땅 저장
cand_list = adj[0]
# heap 구조화시켜 최저 가중치 간선이 제일 앞으로 옴
heapify(cand_list)
# 최소 신장 트리 값을 저장할 MST
MST = 0

while cand_list:
	# 트리에 인접한 간선을 하나씩 꺼내서 (최소 순으로 꺼내진다.)
	w, node = heappop(cand_list)
    	# 간선의 목적지가 트리가 아니면 (cycle 방지)
	if node not in Tree_node:
    		# 정점을 트리에 편입 (가중치가 최소닌까) 
		Tree_node.add(node)
        	# 가중치 추가
		MST += w
        # 트리에 정점이 추가되었으니 트리 인접 간선 추가요
	for e in adj[node]:
    		# 근데 트리면 안댐 ㅋ
    		if e[1] not in Tree_node:
        	# heappush로 넣어서 
            	# 가중치 최소 간선이 제일 앞으로..
        		heappush(cand_list,e)

실행

입력

# TestCase 1
2 3 # V, E
0 1 1 # a, b, W
0 2 1
1 2 6

# TestCase 2
4 7
0 1 9
0 2 3
0 3 7
1 4 2
2 3 8
2 4 1
3 4 8

출력

{0}	#Tree_node
[[1, 1], [1, 2]]	#Cand_list [Weight, Node]
{0, 1}
[[1, 2], [6, 2]]
{0, 1, 2}
[[6, 2]]

2 #MST

----

{0}
[[3, 2], [9, 1], [7, 3]]
{0, 2}
[[1, 4], [7, 3], [8, 3], [9, 1]]
{0, 2, 4}
[[2, 1], [7, 3], [8, 3], [9, 1], [8, 3]]
{0, 1, 2, 4}
[[7, 3], [8, 3], [8, 3], [9, 1]]
{0, 1, 2, 3, 4}
[[8, 3], [8, 3], [9, 1]]
{0, 1, 2, 3, 4}
[[8, 3], [9, 1]]
{0, 1, 2, 3, 4}
[[9, 1]]

13

트리에 인접하고 트리에 속하지 않은 정점들과 이어진 간선들이 잘 보관되어 있다. 어떤 간선들이 선택되는지까지 알고싶다면, 인접 리스트를 [w,a,b] 구조로 저장해야한다. 잘 보면 코드에 정점에 대한 언급이 거의 없다.

특징

정점에 대한 접근이 없이 간선을 힙에 push하고 pop하는 것이 주요 연산
최악의 경우는 모든 간선이 cand_list에 들어가서 while 문을 반복하고 heap 연산을 반복하는 것. 이 때 시간복잡도는 $O(ElogE)$ . E는 최대 $V^2$ 까지 될 수 있으므로 간선이 많다면 오히려 역효과가 날 수도 있다.

정점에 비해 간선이 매우 적다면 인접행렬 접근보다 매우 큰 효율을 보이는 방법

여기서 또 개선을 하면 드더이 시간복잡도가 $O(ElogV)$ 인 Prim 알고리즘을 짤 수 있다는데, 다음 기회에... 난 몰라!

https://ko.wikipedia.org/wiki/%ED%94%84%EB%A6%BC_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

느낀 점

같은 알고리즘에서도 자료구조 및 접근 방법에 따라 시간복잡도가 다른 것이 재밌습니다. 인접 행렬과 힙,인접리스트 접근법, 이 두개만 알아도 문제에 따라서 다르게 잘 사용하여 MST에 대해선 매우 강해졌지 않을까요? 개선된 Prim 알고리즘 공부를 하기 싫어서 그러는 게 아닙니다. 허허

얘가 훨씬 코드가 간결해서 좋았습니다. 파이썬 조아 ㅎㅎ