최소 신장 트리와 Prim 알고리즘

Jeuk Oh·2021년 8월 26일

그래프 알고리즘

알고리즘 정리

목록 보기

3/5

신장 트리 (Spanning Tree)

무향 그래프 중 모든 정점이 연결되어 있고 사이클이 없는 트리
사이클 : 임의의 정점 s에서 출발하여 다른 간선을 통해서 다시 정점 s로 도달하는 경로가 있는 경우.
사이클이 없고 모든 정점이 연결되어있다면, 정점 v개에 대해 간선의 개수가 v-1개가 된다.
한 그래프에 여러 신장 트리를 구하는 것이 가능하다.
DFS나 BFS를 통해서 신장트리를 구할 수 있다.

최소 신장 트리 (MST)

신장 트리 중 간선의 가중치 합이 최소인 신장 트리
단순히 모든 정점의 가중치가 최소인 간선을 V-1개 고르면 -> 사이클이 될 수 있음.
시작 정점에서 가중치가 최소인 간선들만 탐색하며 가면 -> 가중치 합이 최소가 아닐 수 있음.

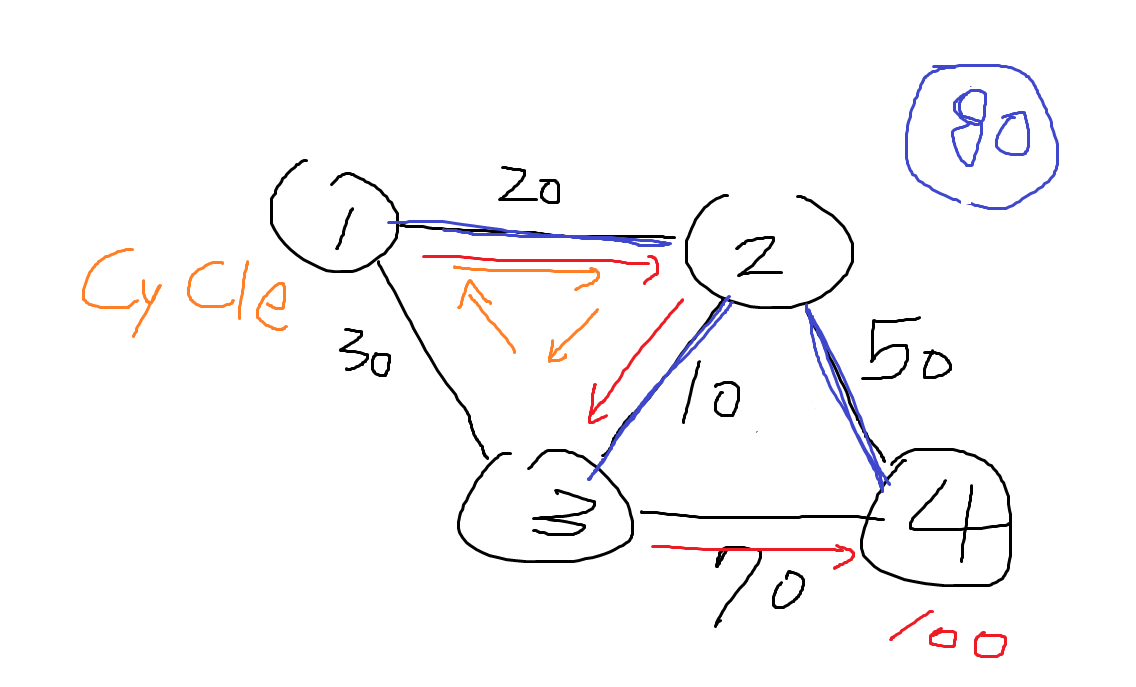
(그림판 ㅈㅅ ㅎㅎ!)

그림처럼 정점과 간선이 주어진 경우,

주황 : 단순히 가중치가 최소인 간선을 V-1개 고른 경우 -> 사이클

빨강 : 시작 정점 1에서 가중치가 최소인 간선들만 통해가는 경우 -> 최소 신장 트리가 아님

파랑 : 올바른 최소 신장 트리

문제 유형 : 모든 정점을 최소 비용으로 연결하는 문제
- 네트워크 연결 (https://www.acmicpc.net/problem/1922)
- 도시 전력, 도로 연결 (https://www.acmicpc.net/problem/6497)

Prim 알고리즘, Kruskal 알고리즘으로 최소 신장 트리를 구할 수 있다.

Prim 알고리즘

한 정점에 연결된 간선 중 하나씩 선택하면서 최소 신장 트리를 완성하는 알고리즘

시작 정점을 루트로 하는 그래프 내 트리를 생각하자
시작 정점에 연결 된 간선 중 최소 가중치로 연결된 정점을 트리에 자손으로 편입
트리에 편입된 정점과 비트리 정점과 연결된 모든 간선 가중치를 확인하고 또 다음 비트리 정점을 편입하러 간다.
모든 비트리 정점들은 트리에 인접할 수 있는 최소 가중치를 업데이트 및 저장 (인접 안할 땐 INF 값)
어떤 비트리 정점을 편입시키느냐 -> 트리에 편입하는 비용이 가장 낮은 비트리 정점.
시작 정점을 제외하고 모든 비트리 정점 V-1개에 대해 1개의 간선을 선택하므로 V-1개의 간선이 선택된다.

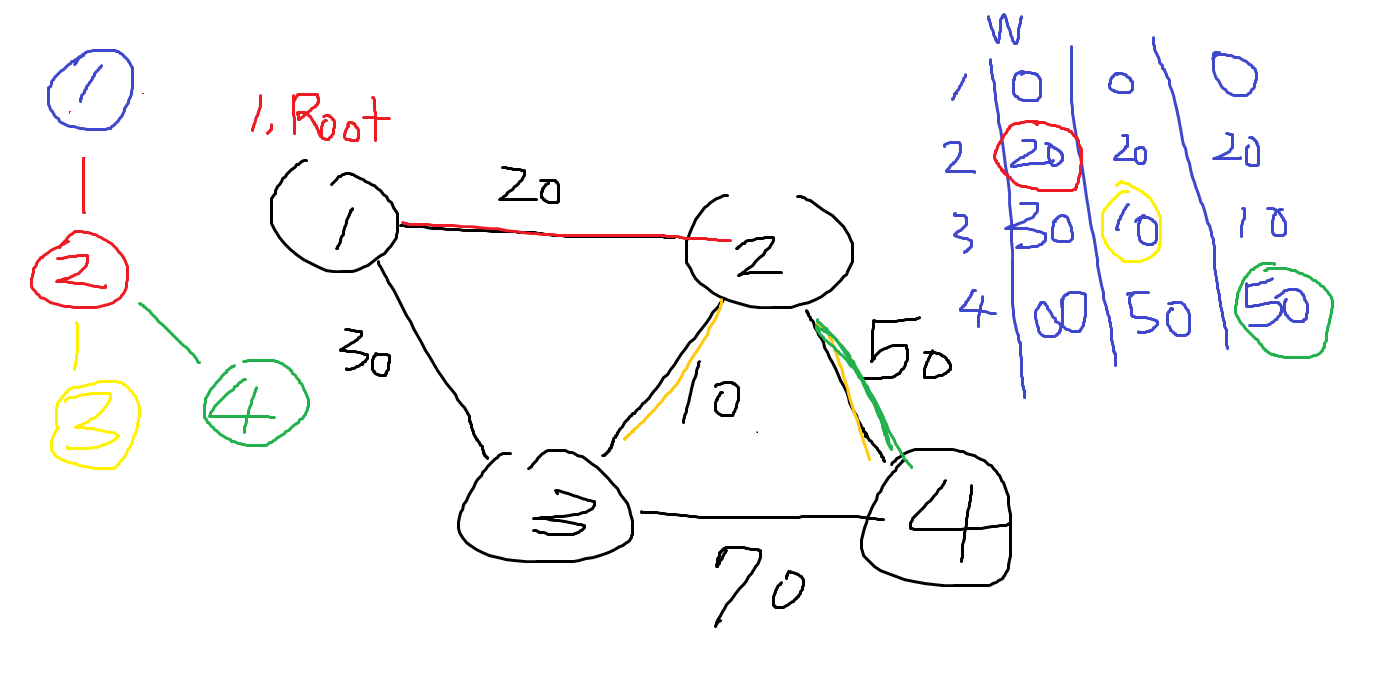
앞 선 예제에 Prim 알고리즘 동작을 그리자면 이런 느낌.
시작 정점이자 트리의 루트인 1번 정점을 시작으로
트리에 연결된 정점의 최소 가중치를 업데이트하고,

최소인
정점을 골라서 트리에 편입 -> 트리가 커졌으니 다시 최소 가중치를 업데이트해서 반복.

구현

앞선 그림 예제를 이용하여 구현해보자.

먼저 인풋을 받아 인접 행렬을 구성하자.

import sys; readline = sys.stdin.readline
N = int(input())
M = int(input())

adj = [[sys.maxsize]*(N+1) for _ in range(N+1)]

for _ in range(M):
    a, b, w = map(int,readline().split())
        adj[a][b] = w
        adj[b][a] = w

다음으로 Prime 알고리즘을 짜자.
시작 정점을 매개변수로 받아. 정점 가중치 배열과 트리에 속해 있는지 확인하는 (visit과 같은 역할이기도 하다.) 배열, 트리를 저장하는 배열을 만들자트리는 부모 정점을 가르키게 해서 저장한다. 주석으로 정리하겠습니다.

def Prime(s):
	# N번째 정점이 트리에 편입하는데 드는 비용을 저장 
   min_adj = [0]+[sys.maxsize]*N
   # 방문처리 -> 방문된 정점은 트리에 편입된 것이기도 함.
   visit = [False]*(N+1)
   # 정점 idx가 1~N+1 까지 이므로 0을 방문처리해서 고려안함
   visit[0] = True
   # 트리를 저장하는 배열, 먼저 자기자신을 루트로 초기화
   root = [i for i in range(N+1)]
   
   # 시작 정점은 트리의 루트가 되므로 비용을 0으로 초기화
   min_adj[s] = 0
   
   # 트리에 편입될 정점을 N번 찾아야함
   for _ in range(N):
   	# min_adj가 최소인 값을 찾기위한, idx
       min_idx = -1
       tmp_min = sys.maxsize

       # 비트리 정점 중 가중치가 최소인 정점 선택
       # 처음엔 모든 정점이 비트리 정점
       # 시작정점 s를 가중치 0으로 설정했으므로
       # 무조건 처음엔 시작정점이 트리로 편입된다.
       for i in range(1,N+1):
       # visit -> 트리인가? 
       # min_adj[i] < tmp_min -> 비트리 정점 중 가중치가 최저인가?
           if not visit[i] and min_adj[i] < tmp_min:
               tmp_min = min_adj[i]
               min_idx = i
       # 트리에 편입될 정점을 찾았으므로 방문 처리
       visit[min_idx] = True

       print(min_idx)
       # 선택된 정점(새로 편입된 정점)에 연결된 간선 들을 확인 -> 간선값 adj_value, 연결된 정점 adj_idx
       for adj_idx, adj_value in enumerate(adj[min_idx]):
       
       # 간선과 연결된 정점이 비트리이며 편입비용이 현 편입비용보다 작다면,
       # 업데이트해주며 새로 편입된 정점을 루트로 정해준다.
           if not visit[adj_idx] and adj_value < min_adj[adj_idx]:
               min_adj[adj_idx] = adj_value
               root[adj_idx] = min_idx
       print(root)
       print(min_adj)

	# 루트 정보를 반환 (문제에 따라 다름)
   return root

실행

입력

4 # V_Number
5 # E_Number
1 2 20 # A, B, Weight
1 3 30
2 3 10
2 4 50
3 4 70

출력

1 # 트리에 편입되는 정점 min_idx
[0, 1, 1, 1, 4] # 트리 상태 root
[0, 0, 20, 30, 9223372036854775807] # 최소편입비용 adj_min 
2
[0, 1, 1, 2, 2]
[0, 0, 20, 10, 50]
3
[0, 1, 1, 2, 2]
[0, 0, 20, 10, 50]
4
[0, 1, 1, 2, 2]
[0, 0, 20, 10, 50]
[0, 1, 1, 2, 2]

그림과 일치한다! 이 예제에서는 min_idx가 2일 때, 모든 루트와 adj_min이 결정되지만 정점 3과 4도 트리에 편입해주면서 간선을 확인해주어야한다.

특징

핵심은 트리와 비트리를 구분하고, 임의의 비트리 정점이 트리에 편입하기 위한 최소 가중치를 업데이트하는 것.

다음 트리 정점에 편입될 비트리 정점을 찾을 때, 최소 가중치가 최저인 정점을 트리에 편입시킨다.

이후 추가된 트리 정점에 연결된 정점들에 대해 최소 가중치를 업데이트

최소 가중치가 업데이트 된다면, 두 정점 (트리 정점과 비트리 정점)의 간선 가중치가 최소이므로 비트리 정점이 트리 정점을 부모 노드로 바라보게 한다.

비트리 정점들 중 트리 정점으로 편입할 때는

시간복잡도는 편입될 정점 V개를 정하고, 인접행렬에서 간선의 개수를 검색하는데 V개의 연산이 필요하므로 $O(V^2)$

위키에 따르면, 인접 행렬이 아닌 이진 힙 + 인접 리스트를 사용하면 $O(ElogV)$ ,

피보나치 힙을 사용한다면 $O(E+VlogV)$ 까지 줄일 수 있다고 한다.

아이고 난 몰라!

https://ko.wikipedia.org/wiki/%ED%94%84%EB%A6%BC_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

추가문제

https://www.acmicpc.net/problem/1922

네트워크 문제를 풀어보며 구현해보자.

문제

도현이는 컴퓨터와 컴퓨터를 모두 연결하는 네트워크를 구축하려 한다. 하지만 아쉽게도 허브가 있지 않아 컴퓨터와 컴퓨터를 직접 연결하여야 한다. 그런데 모두가 자료를 공유하기 위해서는 모든 컴퓨터가 연결이 되어 있어야 한다. (a와 b가 연결이 되어 있다는 말은 a에서 b로의 경로가 존재한다는 것을 의미한다. a에서 b를 연결하는 선이 있고, b와 c를 연결하는 선이 있으면 a와 c는 연결이 되어 있다.)

그런데 이왕이면 컴퓨터를 연결하는 비용을 최소로 하여야 컴퓨터를 연결하는 비용 외에 다른 곳에 돈을 더 쓸 수 있을 것이다. 이제 각 컴퓨터를 연결하는데 필요한 비용이 주어졌을 때 모든 컴퓨터를 연결하는데 필요한 최소비용을 출력하라. 모든 컴퓨터를 연결할 수 없는 경우는 없다.

입력

첫째 줄에 컴퓨터의 수 N (1 ≤ N ≤ 1000)가 주어진다.

둘째 줄에는 연결할 수 있는 선의 수 M (1 ≤ M ≤ 100,000)가 주어진다.

셋째 줄부터 M+2번째 줄까지 총 M개의 줄에 각 컴퓨터를 연결하는데 드는 비용이 주어진다. 이 비용의 정보는 세 개의 정수로 주어지는데, 만약에 a b c 가 주어져 있다고 하면 a컴퓨터와 b컴퓨터를 연결하는데 비용이 c (1 ≤ c ≤ 10,000) 만큼 든다는 것을 의미한다. a와 b는 같을 수도 있다.

출력

모든 컴퓨터를 연결하는데 필요한 최소비용을 첫째 줄에 출력한다.

풀이

앞서 사용한 Prim 알고리즘에서

root 배열은 각 정점마다 연결 된 부모 정점을 저장하고있다. 자기 자신을 부모로 하지 않는 경우에만 정점과 부모 정점을 연결하는 간섭 가중치를 합해주기만 하면 완성

	anw = 0
    for idx, r in enumerate(root):
        if idx==r: continue
        anw += adj[idx][r]
    return anw

Prim 함수 안의 해당 코드만 추가해주면 된다.

느낀 점

아직 코드를 따라 적는 수준밖에 안 되어서 더욱 연습 문제를 많이 풀어봐야겠습니다. 글을 쓰면서 그래도 이해는 확실히 되었습니다. 굳

연습문제를 몇 개 풀어보고 다음은 MST를 구하는 다른 알고리즘인 Kruskal 알고리즘을 공부해보겠습니다.

Jeuk Oh

개발을 재밌게 하고싶습니다.

이전 포스트

문자열 패턴매칭

다음 포스트