2021-03-16
알고리즘
그래프
선형 1:1, 한줄로 세울 수 있다.
비선형 1:1 아닌 관계 (1:多 ,多:多)
→ 트리(계층적) (1:多)
→ 그래프 (多:多)
그래프
- 아이템(사물 또는 추상적 개념)들과 이들 사이의 연결관계를 표현한다.
- 정점(Vertex) : 그래프의 구성요소로 하나의 연결점 (트리에서는 노드)
- 간선(Edge) : 두 정점을 연결하는 선
- 차수(Degree) : 정점에 연결된 간선의 수
- 그래프는 정점들의 집합과 이들을 연결하는 간선들의 집합으로 구성된 자료구조
- V : 정점의 개수, E: 그래프에 포함된 간선의 개수
- V개의 정점을 가지는 최대 간선 V*(V-1)/2 간선이 가능하다( 무향 그래프일때 V(V-1)/2 , 유향 그래프 V(V-1) )
- 예) 5개 정점이 있는 유향 그래프의 최대 간선수는 10(⇒5*4/2) 개 이다.
그래프 유형
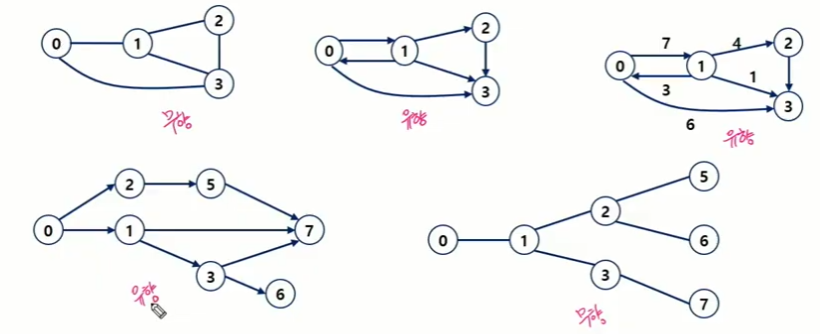
-
무향 그래프
방향성 無 → 양방향 관계
-
유향 그래프
방향성 有 → 단방향 관계
-
가중치 그래프
관계의 정도를 수치로 표현한 그래프
-
사이클 없는 방향 그래프
4번째 그래프.
.png)
-
부분 그래프
원래 그래프에서 일부의 정점이나 간선을 제외한 그래프
-
완전 그래프
-
정점들에 대해 가능한 모든 간선을 가진 그래프
V개의 정점 에 V-1개 간선을 갖는 그래프
-
-
트리는 싸이클이 없는 무향 연결 그래프이다.
두 노드 사이에는 유일한 경로가 존재한다.
각 노드는 최대 하나의 부모 노드가 존재
각 노드는 자식노드가 없거나 하나 이상이 존재 할 수 있다.
그래프 경로
-
인접
두 개의 정점에 간선이 존재(연결됨)하면 서로 인접해 있다고 한다.
완전 그래프에 속한 임의의 두 정점들은 모두 인접해 있다.
.png)
-
경로
-
어떤 정점에서 시작하여 다른 정점B로 끝나는 순회로 두 정점사이를 잇는 간선들을 순서대로 나열한것
→(유향그래프)
-
0~6의 경로
→ 정점들 0-2-4-6
→ 간선들 (0,2) , (2,4) ,(4,6)
-
경로 중 한 정점을 최대 한번만 지나는 경로를 단순경로
-
순환경로(cyclic path)
경로의 시작점과 끝점이 같음
경로에서 어떤 정점을 두 번이상 거치는경우
-
그래프 표현
간선의 정보를 저장하는 방식, 메모리나 성능을 고려해서 결정
DFS/BFS/다익스트라는 인접행렬,인접리스트,간선리스트 3개다 풀 수 있지만,
3개의 방법중에서 인접 리스트가 가장 효율적인 방법이라 다른 방식은 특별한 케이스 아니면 사용안해요
그러니 그래프 문제 푸실 때 특별한 경우 아니면 인접리스트로 사용하는 것이 좋습니다 :)
.png)
인접행렬(Adjacent matrix) →플로이드 와샬 (정점 중심)
VxV 크기의 2차원 배열을 이용해서 간선 정보를 저장
배열의 배열
-
두 정점을 연결하는 간선의 유무를 행렬로 표현
-
VxV 정방행렬
행 번호와 열 번호는 그래프의 정점에 대응
두 정점이 인접되어 잇으면 1, 그렇지 않으면 0으로 표현
-
무향 그래프
i 번쨰 행의 합 = i 번째 열의 합 = Vi의 차수 → 0이 아닌것의 갯수의 합
-
유향 그래프
행 i의 합 = Vi의 진출 차수
열 i의 합 = Vi의 진입 차수
→ 이둘의 합친게 정점 i에서의 차수
-
인접 행렬의 단점
희소 그래프(정점 많고, 간선은 적은)
→ 공간복잡도도 영향을 주지만 정점을 탐색을 할 때도 정점수 만큼 탐색 → 시간 , 공간 비효율
VS
밀집 그래프(정점 , 간선 비례 해서 많다)
⇒ 희소 그래프 일때는 인접 리스트를 쓰자
.png)
인접 리스트(Adjacent List) → DFS,BFS, 다익스트라 (정점 중심)
-
각 정점에 대한 인접 정점들을 순차적으로 표현
→인접한 정점만 목록으로 유지한다. (LinkedList로 표현)
-
각 링크는 목록을 유지를 위한 링크(포인터) → 연결되어 있다는 의미 아님
-
정점에 비해 간선이 상대적으로 적은 경우 유리.
.png)
- 연결리스트로 만듬→ head를 넣을 부분(from)을 Node[]로 선언
- arrayList → head를 넣을 부분(from)을 Arraylist[] 로 선언
⇒ 서로 순서가 상관 없다.
.png)
무향 그래프 노드 수 = 간선의 수 * 2
각 정점의 노드 수 = 정점의 차수
방향 그래프 노드 수 = 간선의 수
각 정점의 노드수 = 정점의 진출 차수
→ 진입 차수를 찾기 위해서는 모든 정점들에서 내가 존재하는지 찾는다 .
간선 리스트(Edge List) → 최소신장 트리 (간선 중심)
.png)
- 두 정점에 대한 간선 그 자체를 객체로 표현하여 리스트로 저장
- 간선을 표현하는 두 정점의 정보를 나타냄(시작 정점, 끝 정점)
그래프 탐색 (순회)
-
그래프 순회는 비선형구조인 그래프로 표현된 모든 자료(정점)를 빠짐없이 탐색하는 것을 의미한다.
-
두가지 방법
너비 우선 탐색
깊이 우선 탐색
BFS
너비 우선 탐색은 탐색 시작점의 인접한 정점들을 먼저 모두 차례로 방문한 후에, 방문 했던 정점을 시작점으로 하여 다시 인접한 정점들을 차례로 방문하는 방식
인접한 정점들에 대해 탐색을 한 후 , 차례로 다시 너비 우선 탐색을 진행해야 하므로, 선입 선출 형태의 자료구조인 큐를 활용함
예)
.png)
초기 상태
-
visted 배열 생성 및 false로 초기화
트리 와는 다르게 visted 배열을 이용해서 사이클이 발생하는것을 방지
→ 트리는 사이클이 존재 하지 않아서 visted 배열이 필요 없었다.
→ (큐에 넣을때 미리 방문 햇다는 체크를 한다)
-
Q생성
-
시장 정점(A) 방문처리 및 Enqueue
인접 리스트 BFS
package com.study34;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
/*
7
8
0 1
0 2
1 3
1 4
2 4
3 5
4 5
5 6
*/
//먼저 인접 그래프를 만들고 그래프를 Q를 이용하여 탐색 할 예정
public class G2_인접리스트2 {
static int N,start,result;
static boolean [][] adjMatrix;
static Node[] adjList; //인접리스트에 헤드의 역할을 하는 리스트 생성
static class Node{
int vertex;
Node next;
public Node(int vertex) {
this.vertex = vertex;
}
public Node(int vertex, Node next) {
this.vertex = vertex;
this.next = next;
}
@Override
public String toString() {
StringBuilder builder = new StringBuilder();
builder.append("Node [vertex=");
builder.append(vertex);
builder.append(", next=");
builder.append(next);
builder.append("]");
return builder.toString();
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N = Integer.parseInt(br.readLine());
int C =Integer.parseInt(br.readLine());
//LinkedList<Integer> graph = new LinkedList<>();
adjList = new Node[N];
for (int i = 0; i < C; i++) {
st = new StringTokenizer(br.readLine()," ");
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
//from에 해당 하는 헤드에 to 값을 넣고 헤드의 next를 새로 들어오는 값의 next로 넣는다.
adjList[from] = new Node(to, adjList[from]);
//무향 그래프 인경우 반대도 같이 해준다.
adjList[to] = new Node(from, adjList[to]);
}
BFS();
}
public static void BFS() {
Queue<Integer> que =new LinkedList<>();
boolean[] visited =new boolean[N];
//탐색 시작 정점: 0으로 출발
int start = 0;
que.offer(start);
visited[start]=true;
while(!que.isEmpty()) {
int current = que.poll();
//꺼내서 하고 싶은 작업 처리
System.out.println((char)(current+65));
//인접 정점 탐색
for (Node temp = adjList[current]; temp !=null; temp=temp.next) {
//인접 정점만 반복처리
if(!visited[temp.vertex]) {
que.offer(temp.vertex);
visited[temp.vertex] = true;
}
}
}
}
}DFS 알고리즘 (재귀)
public static void DFS(int current) {
visited[current] = true;
//꺼내서 하고 싶은 작업 처리
System.out.println((char)(current+65));
for (Node temp = adjList[current]; temp !=null; temp=temp.next) {
//인접 정점만 반복처리
//이미 인접한 애들만 붙어 있으니 인접 체크 할 필요 없다.
if(!visited[temp.vertex]) {
//visted[current] = true;
//위에 처럼 방문 하기 전에만 체크해주려고 하면
//DFS들어오기전에 들어오는 0번 인덱스를 방문 체크 해야한다.
//83번 줄
DFS(temp.vertex);
}
}
}가중치가 있는 그래프 정보에 대해서 인접행렬을 이용할 경우 0: 인접 x → 0이 아닌값 : 인접 O
0 : 가중치 x
0이 아닌값 가중치 O
서로소 집합 (Disjoint-set) → (Union - find) 알고리즘
서로소 또는 상호배타 집합들은 서로 중복 포함된 원소가 없는 집합들이다. 다시 말해 교집합이 없다.
집합에 속한 하나의 특정 멤버(구분자)를 통해 각 집합들을 구분한다
⇒ 대표자(구분자)
- 서로소 집합을 표현하는 방법
- 연결리스트
- 트리
- 서로소 집합 연산
- Make-Set(x)
- Find-Set(x)
- Union(x,y)
서로소 집합 표현 (연결리스트)
- 같은 집합의 원소들은 하나의 연결리스트로 관리한다.
- 연결리스트의 맨 앞의 원소를 집합의 대표 원소로 삼는다.
- 각 원소는 집합의 대표원소를 가리키는 링크를 갖는다.
.png)
.png)
연결리스트의 연산의 예
find-Set(e) → return a
Find-Set(f) → return b
Union(a,b)
package com.study34;
import java.lang.reflect.Array;
import java.util.Arrays;
public class DisjointSetTest {
static int N;
static int parents[];
static void make() {
//크기가 1인 단위 집합을 만든다.
for (int i = 0; i < N; i++) {
parents[i] = i;
}
}
static int findSet(int a) {
//들오온 a가 대표자라면
if(parents[a]==a) return a;
// return findSet(parents[a]); //path compression 전
return parents[a] = findSet(parents[a]); //path compression 후
}
static boolean union(int a, int b) {
//각 집합의 대표자들 가지고 오기.
int aRoot = findSet(a);
int bRoot = findSet(b);
//이미 같은 집합인 경우 (대표자가 같은경우)
if(aRoot == bRoot) return false;
//두 집합의 대표자가 다른경우 하나의 집합으로 합친다.
parents[bRoot] = aRoot;
// 하나의 집합으로 합쳐 졌다.
return true;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
N = 5;
parents = new int[N];
//1.make set
make();
System.out.println("===============union================");
System.out.println(union(0,1));
System.out.println(Arrays.toString(parents));
System.out.println(union(1,2));
System.out.println(Arrays.toString(parents));
System.out.println(union(3,4));
System.out.println(Arrays.toString(parents));
System.out.println(union(0,2));
System.out.println(Arrays.toString(parents));
System.out.println(union(0,4));
System.out.println(Arrays.toString(parents));
System.out.println("===============union================");
System.out.println(findSet(4));
System.out.println(Arrays.toString(parents));
System.out.println(findSet(3));
System.out.println(Arrays.toString(parents));
System.out.println(findSet(2));
System.out.println(Arrays.toString(parents));
System.out.println(findSet(0));
System.out.println(Arrays.toString(parents));
System.out.println(findSet(1));
System.out.println(Arrays.toString(parents));
}
}
서로소 집합 표현 (트리)
.png)
전처리 연산 → 단위 집합으로 만든다 (크기가 1인 집합)
.png)
Make-Set(X) : 유일한 멤버 x를 포함하는 새로운 집합을 생성하는 연산
Find_Set(x) : x를 포함하는 집합을 찾는 연산
Union(x,y) : x와 y를 포함하는 두 집합을 통합하는 연산
연산의 효율을 높이는 방법
-
Rank를 이용한 Union
각 노드는 자신을 루트로 하는 subtree의 높이를 랭크라는 이름으로 저장한다.
두 집합을 합칠 때 랭크가 낮은 집합을 rank가 높은 집합에 붙인다.
-
Path Compression
Find-set을 행하는 과정에서 만나는 모든 노드들이 직접 Root를 가리키도록 포인터를 바꾸어 준다.
랭크를 이용한 Union의 예
.png)
최소 신장 트리 (MST)
-
그래프에서 최소 비용 문제
모든 정점에 연결하는 간선들의 가중치(비용)의 합이 최소가 되는 트리 → 최소 신장 트리
두 정점 사이의 최소 비용의 경로 찾기
-
신장 트리
n개의 정점으로 이루어진 무향 그래프에서 n개의 정점과 n-1개의 간선으로 이루어진 트리
-
최소 신장 트리(Mini1mum Spanning Tree)
크루스칼 알고리즘
-
간선을 하나씩 선택해서 MST를 찾는 알고리즘
-
탐욕적인 방법(greedy method) 을 이용하여 네트워크(가중치를 간선에 할당한 그래프)의 모든 정점을 최소 비용으로 연결하는 최적 해답을 구하는 것
-
탐욕적인 방법
결정을 해야 할 때마다 그 순간에 가장 좋다고 생각되는 것을 선택함으로써 최종적인 해답에 도달하는 것
탐욕적인 방법은 그 순간에는 최적이지만, 전체적인 관점에서 최적이라는 보장이 없기 때문에 반드시 검증해야 한다.
**다행히 Kruskal 알고리즘은 최적의 해답을 주는 것으로 증명되어 있다.
Kruskal 알고리즘의 동작
- 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
- 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다.
- 즉, 가장 낮은 가중치를 먼저 선택한다.
- 사이클을 형성하는 간선을 제외한다.
- 해당 간선을 현재의 MST(최소 비용 신장 트리)의 집합에 추가한다.
→ 간선 리스트를 사용한다.
.png)
-
최초, 모든 간선을 가중치에 따라 오름차순으로 정렬 ⇒간선 리스트를 작성최초, 모든 간선을 가중치에 따라 오름차순으로 정렬 ⇒간선 리스트를 작성
-
가중치가 가장 낮은 간선부터 선택하면서 트리를 증가시킴 → 두 정점을 연결하는 의미가 있다.
-사이클이 존재하면 다음으로 가중치가 낮은 간선 선택 → 사이클이 존재한다 ⇒ 트리가 될수 없다
-
n-1개의 간선이 선택될 때까지 2를 반복
package com.study35;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class MST1_kuruskalTest {
static int V,E;
static int parents[];
static Edge[] edgeList;
static class Edge implements Comparable<Edge> {
int from,to,weight;
public Edge(int from, int to, int weight){
super();
this.from = from;
this.to = to;
this.weight = weight;
}
@Override
public int compareTo(Edge o) {
// TODO Auto-generated method stub
//return this.weight - o.weight;
//값이 음수가 나올 수 도 잇다면
return Integer.compare(this.weight, o.weight);
}
}
static void make() {
//크기가 1인 단위 집합을 만든다.
for (int i = 0; i < V; i++) {
parents[i] = i;
}
}
static int findSet(int a) {
//들오온 a가 대표자라면
if(parents[a]==a) return a;
// return findSet(parents[a]); //path compression 전
return parents[a] = findSet(parents[a]); //path compression 후
}
static boolean union(int a, int b) {
//각 집합의 대표자들 가지고 오기.
int aRoot = findSet(a);
int bRoot = findSet(b);
//이미 같은 집합인 경우 (대표자가 같은경우)
if(aRoot == bRoot) return false;
//두 집합의 대표자가 다른경우 하나의 집합으로 합친다.
parents[bRoot] = aRoot;
// 하나의 집합으로 합쳐 졌다.
return true;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
parents = new int[V];
edgeList = new Edge[E];
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
edgeList[i] = new Edge(from,to,weight);
} // 간선리스트
//1.간선리스트 가중치 기준 오름차순 정렬
Arrays.sort(edgeList);
make();
int result = 0;
int count = 0; //선택한 간선수
for (Edge edge : edgeList) {
if(union(edge.from, edge.to)) //사이클 발생 x
result += edge.weight;
if(++count ==V-1) break;
}
System.out.println(result);
}
}
PRIM 알고리즘
시작 정점에서부터 출발하여 신장트리 집합을 단계적으로 확장해나가는 방법
- 정점을 중심으로 해결하는 알고리즘→ 그래프 자료구조 : 인접행렬 , 인접 리스트
- N개의 정점을 모두 고립되지 않도록 연결, 가중치의 합 " 최소 "
Prim 알고리즘의 동작
- 시작 단계에서는 시작 정점만이 MST(최소 비용 신장 트리) 집합에 포함된다.
- 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다.
- 즉, 가장 낮은 가중치를 먼저 선택한다.
위의 과정을 트리가 (N-1)개의 간선을 가질 때까지 반복한다.
