🌈 Graph & Tree 이해
🔥 Graph & Tree 란?
🔥 Graph 표현하기
🔥 인접 리스트 탐색하기(DFS, BFS)
🔥 Graph 예제 풀이
1. Graph & Tree 란?
1) Graph 란?
- Graph란 정점(vertext, node) 와 간선(edge)으로 이루어진자료 구조를 의미함
- Graph는 G(V,E)로 표현하고, 객체와의 관계만 보고 동일한 그래프인지 판단함
- Graph는 무향 그래프와 유향 그래프(방향 그래프)로 구분함
- 무향 그래프 : edge(간선) 사이에 방향이 없는 일반적인 그래프
- 방향 그래프 : edge(간선) 사이에 방향이 존재하는 그래프
- 이 외에 가중치 그래프는 간선에 시간과 거리 등의 가중치가 존재하는 그래프를 뜻함
- 차수(degree) : 차수는 한 vertext(정점)에 연결된 edged(간선)의 수
- 경로(path) : edge와 edge를 잇는 일련의 vertext들
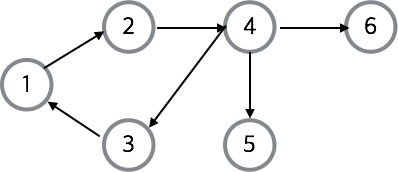
- 싸이클(cycle) : 경로의 한 종류로 한 vertext에서 다시 그 vertext로 돌아오는 경로
- 아래 그림에서 4 -> 3 -> 1 -> 2는 경로이면서 싸이클임
2) Tree 란?
- Tree는 Graph의 한 종류로 싸이클이 없는 연결 Graph임
- 즉, 경로만 있고 순회하여 다시 그 점으로 돌아올 수 없는 Graph를 뜻함
- Tree는
edge = vertex -1조건을 무조건 만족해야하고, 부모와 자식간의 관계가 존재
2. Graph 표현하기
- Graph를 표현하는 방법은 "인접 행렬" 방법과 "인접 리스트" 방법으로 나뉨
1) 인접 행렬
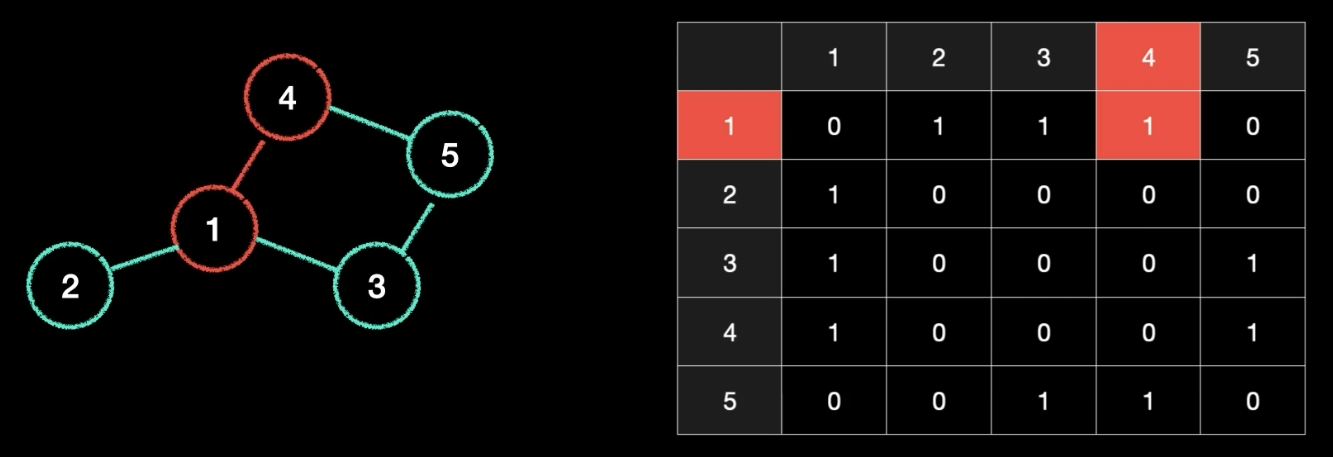
- vertext가 연결되어 있으면(갈 수 있는 길이 있으면) 1, 없으면 0으로 표시하여 행렬을 구성하는 것을 "인접 행렬"이라함
- 1에서 1로 갈수없기 때문에 0(자기 자신은 0으로 표시), 1에서 4 갈 수있기 때문에 1로 표시
- 무향 그래프에서는 양방향으로 갈 수 있기 때문에 인접 행렬은 대각선으로 서로 일치함
- 인접 행렬 구현 예시
""" - 3 - 1 - 0 4 - 2 - """ n = 5 # node(vertex) 갯수 d = [ [ 0 for i in range(n) ] for j in range(n)] # 초기 세팅 # 연결된 행렬 위치에 1을 삽입 d[1][0] = d[0][1] = 1 # 1과 0은 연결, 0과 1은 연결되어 1 d[0][3] = d[3][0] = 1 # 0과 3은 연결, 3과 0은 연결되어 1 d[0][2] = d[2][0] = 1 # 0과 2은 연결, 2과 0은 연결되어 1 d[3][4] = d[4][3] = 1 # 3과 4은 연결, 4과 3은 연결되어 1 d[2][4] = d[4][2] = 1 # 2과 4은 연결, 4과 2은 연결되어 1 for i in range(n): print(d[i]) """ [0, 1, 1, 1, 0] [1, 0, 0, 0, 0] [1, 0, 0, 0, 1] [1, 0, 0, 0, 1] [0, 0, 1, 1, 0] """
2) 인접 리스트
- 한 vertext가 연결되어있는 vertext들을 리스트로 갖고 있는 것을 인접 리스트라함
- vertext 1에서 연결되어있는 vertext는 2,3,4이고, vetext 2에서는 1만 연결됨
- 인접 그래프 구현 예시
""" - 3 - 1 - 0 4 - 2 - """ n = 5 # node(vertex) 갯수 d = [ [] for i in range(n) ] # 초기 세팅(정점 갯수만큼 리스트 생성) d[0].append(1) # 0번 정점을 1,2,3과 연결 d[0].append(2) d[0].append(3) d[1].append(0) # 1번 정점을 0과 연결 d[2].append(0) # 2번 정점을 0,4과 연결 d[2].append(4) d[3].append(0) # 3번 정점을 0,4과 연결 d[3].append(4) d[4].append(3) # 4번 정점을 2,3과 연결 d[4].append(2) for i in range(n): print(i, d[i]) """ 0 [1, 2, 3] 1 [0] 2 [0, 4] 3 [0, 4] 4 [3, 2] """
3) 인접 행렬 vs 인접 리스트
- 인접 행렬은 연결 여부(1과 0)를 2차원 배열만큼을 전부다 갖고 있는 것이고, 연결 리스트는 연결되어 있는 vertex만을 리스트로 갖고 있음
- 인접 행렬의 장점은 두 정점(vertext, node)의 연결 관계를 바로 확인 가능
- 단, 인접 행렬의 단점으로는 인접한 점점을 효율적으로 찾기 힘들고, 메모리 낭비가 큼
- 인접 리스트를 순회해야지만 두 정점(vertext, node)의 연결 관계를 확인할 수 있는 단점이 있으나, 메모리 사용량이 적고 인접한 정점을 찾을 때는 인접 행렬보다 효율적임
- 두 vertext가 연결관계를 가지는지 찾는 시간 복잡도
- 인접 행렬 : O(1)
- 인접 리스트 : O(V)
3. 인접 리스트 탐색하기(DFS, BFS)
1) DFS
""" - 3 - 1 - 0 4 - 2 - """ n = 5 # node(vertex) 갯수 d = [ [] for i in range(n) ] # 초기 세팅(정점 갯수만큼 리스트 생성) d[0].append(1) # 0번 정점을 1,2,3과 연결 d[0].append(2) d[0].append(3) d[1].append(0) # 1번 정점을 0과 연결 d[2].append(0) # 2번 정점을 0,4과 연결 d[2].append(4) d[3].append(0) # 3번 정점을 0,4과 연결 d[3].append(4) d[4].append(3) # 4번 정점을 2,3과 연결 d[4].append(2) # """ # 0 [1, 2, 3] # 1 [0] # 2 [0, 4] # 3 [0, 4] # 4 [3, 2] # """ def dfs(d, pos, vis): # d = 연결 리스트 # pos = 현재 탐색하고 있는 정점 번호 if vis[pos]: return print(pos) vis[pos] = True for i in range(len(d[pos])): # d[pos][i] = 현재 보고 있는 pos 정점의 연결되어이 있는 정점들 dfs(d, d[pos][i], vis) vis = [False for i in range(n)] dfs(d,0,vis)
2) BFS
""" - 3 - 1 - 0 4 - 2 - """ from queue import deque # push def queue_push(q, value): q.append(value) # pop def queue_pop(q): return q.popleft() n = 5 # node(vertex) 갯수 d = [ [] for i in range(n) ] # 초기 세팅(정점 갯수만큼 리스트 생성) d[0].append(1) # 0번 정점을 1,2,3과 연결 d[0].append(2) d[0].append(3) d[1].append(0) # 1번 정점을 0과 연결 d[2].append(0) # 2번 정점을 0,4과 연결 d[2].append(4) d[3].append(0) # 3번 정점을 0,4과 연결 d[3].append(4) d[4].append(3) # 4번 정점을 2,3과 연결 d[4].append(2) # """ # 0 [1, 2, 3] # 1 [0] # 2 [0, 4] # 3 [0, 4] # 4 [3, 2] # """ q = deque() queue_push(q,0) vis = [False for i in range(n)] vis[0] = True while len(q) != 0: front = queue_pop(q) print(front) for i in range(len(d[front])): # d[front][i] : 연결되어있는 정점들 if vis[d[front][i]]: continue vis[d[front][i]] = True queue_push(q, d[front][i])
4. Graph 예제 풀이
1) boj 2606번 : 바이러스(https://www.acmicpc.net/problem/2606)
- 인접 리스트 구현 방법
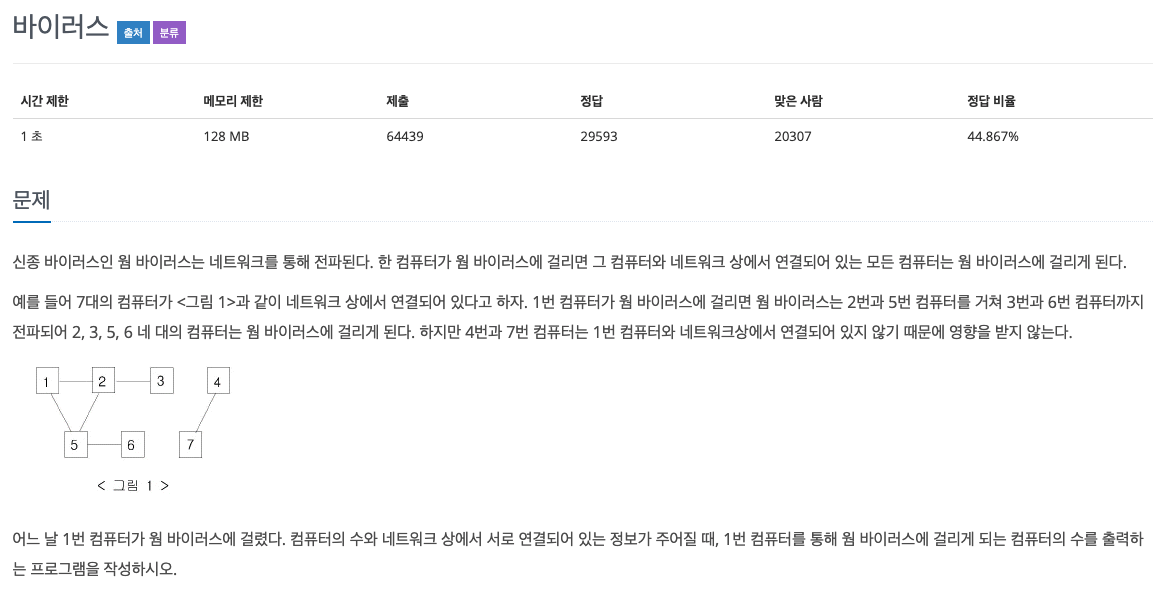
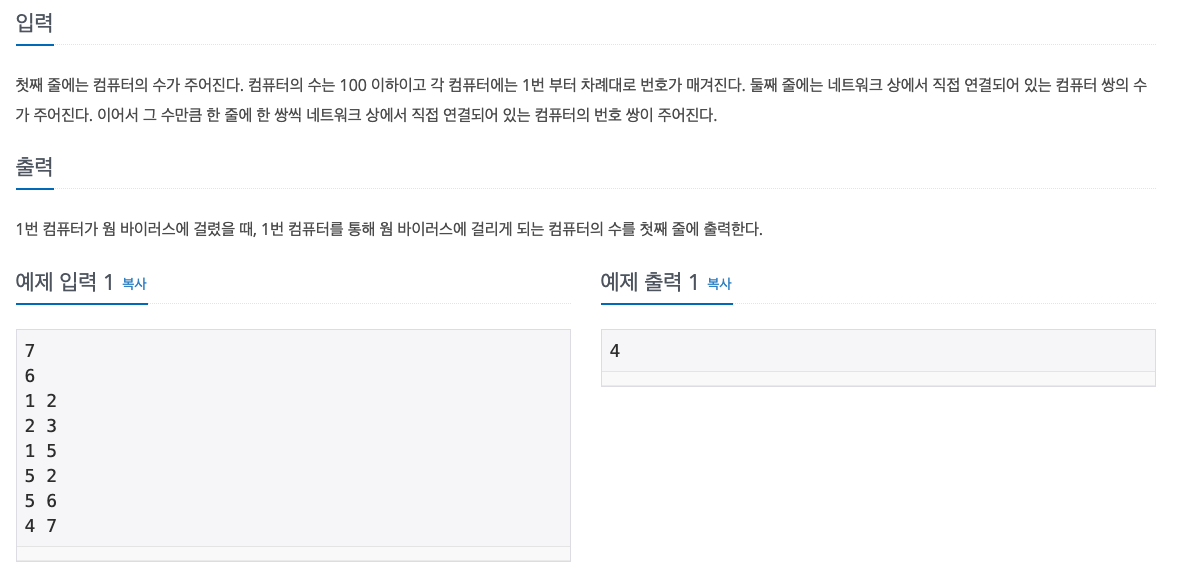
""" 7 6 1 2 2 3 1 5 5 2 5 6 4 7 """ import sys n = int(sys.stdin.readline()) # 컴퓨터 수 m = int(sys.stdin.readline()) # 연결된 쌍의 수 d = [[] for i in range(n+1)] for i in range(m): # 0,1,2,3,4,5 s, e = list(map(int, sys.stdin.readline().split())) # 서로 연결하는 방법 d[s].append(e) d[e].append(s) # d 상태 확인 for i in range(1, n+1): print(i, d[i]) """ 1 [2, 5] 2 [1, 3, 5] 3 [2] 4 [7] 5 [1, 2, 6] 6 [5] 7 [4] """# boj 2606 : 바이러스 """ 7 6 1 2 2 3 1 5 5 2 5 6 4 7 """ import sys from queue import deque # queue_push def queue_push(q, v): q.append(v) # queue_pop def queue_pop(q): return q.popleft() n = int(sys.stdin.readline()) # 컴퓨터 수 m = int(sys.stdin.readline()) # 연결된 쌍의 수 d = [[] for i in range(n+1)] for i in range(m): # 0,1,2,3,4,5 s, e = list(map(int, sys.stdin.readline().split())) d[s].append(e) d[e].append(s) ans = 0 visited = [False for i in range(n+1)] q = deque() queue_push(q, 1) visited[1] = True while len(q) != 0: ans += 1 front = queue_pop(q) for i in range(len(d[front])): if visited[d[front][i]]: continue visited[d[front][i]] = True queue_push(q, d[front][i]) print(ans-1) # 4
2) boj 1260번 : DFS와 BFS(https://www.acmicpc.net/problem/1260)
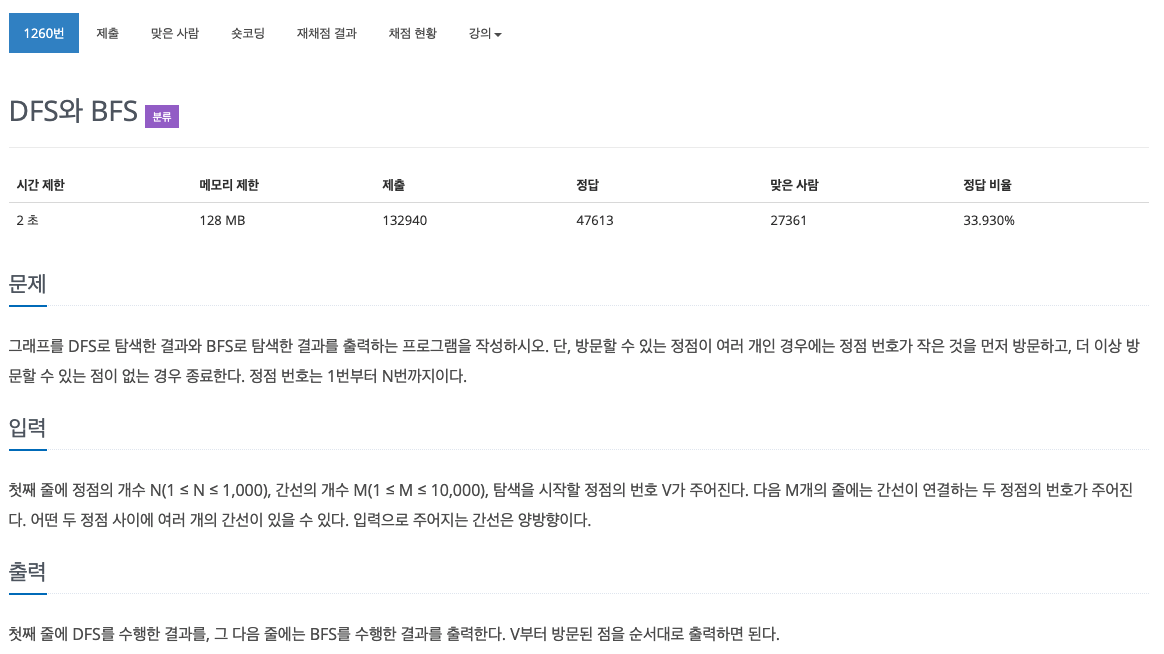
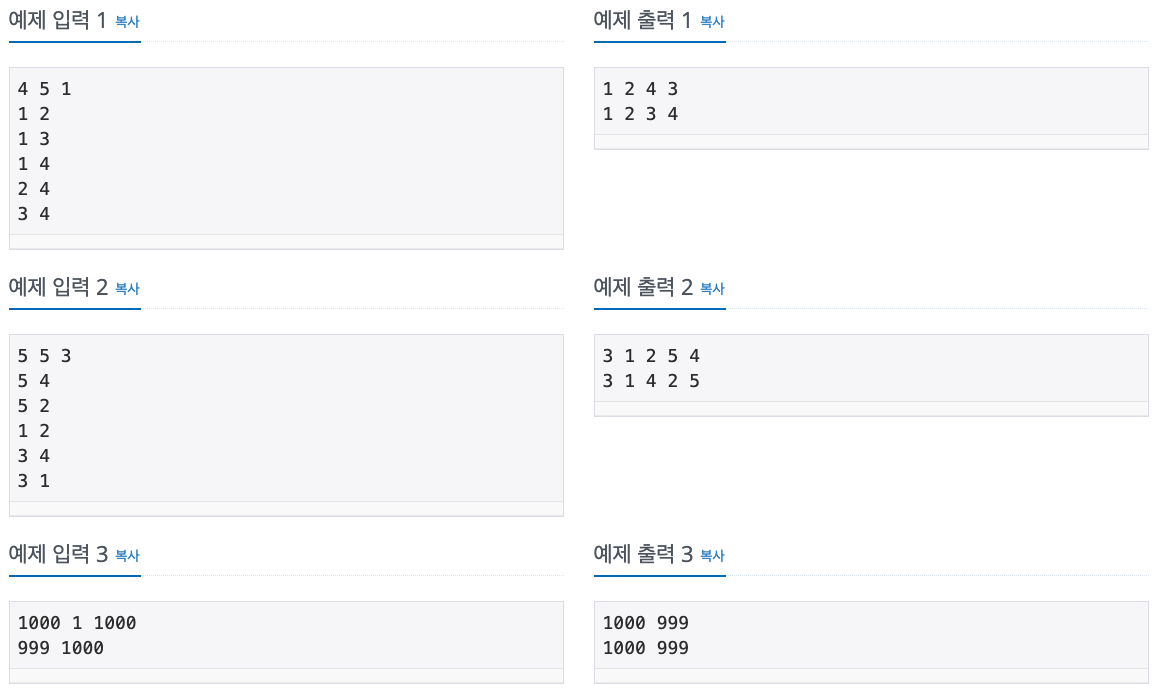
# boj 1260 : DFS와 BFS """ 4 5 1 1 2 1 3 1 4 2 4 3 4 """ import sys N, M, V = map(int, sys.stdin.readline().split()) d = [ [] for i in range(N+1)] for i in range(M): s,e = list(map(int, sys.stdin.readline().split())) d[s].append(e) d[e].append(s) # 가장 작은것 부터 방문하기 위해, 첫번째를 제외하고 sort for i in range(1, N+1): d[i].sort() # for i in range(N+1): # print(i, d[i]) # DFS def dfs(d, pos, vis): print(pos, end=' ') vis[pos] = True for i in range(len(d[pos])): if vis[d[pos][i]]: continue dfs(d, d[pos][i], vis) # BFS from queue import deque def queue_push(q, value): q.append(value) def queue_pop(q): return q.popleft() def bfs(N, d, V): vis = [False for i in range(N+1)] q = deque() queue_push(q, V) vis[V] = True while len(q) != 0: front = queue_pop(q) print(front, end=' ') for i in range(len(d[front])): if vis[d[front][i]]: continue vis[d[front][i]] = True queue_push(q, d[front][i]) vis = [False for i in range(N+1)] dfs(d, V, vis) print() bfs(N, d, V) """ 1 2 4 3 1 2 3 4 """
Keep Going, Keep Coding!