🌈 하노이의 탑(Tower of Hanoi)
🔥 하노이 탑 문제 설명
🔥 하노이 탑 문제 과정
🔥 핵심 아이디어 정리
🔥 재귀 호출 과정 요약
🔥 하노의 탑 최종 코드
1. 하노이 탑 문제 설명
- 하노이의 탑은 프랑스 수학자 에두아르드가 처음으로 발표한 게임입니다. 하노이의 탑은 A, B, C 3개의 기둥과 기둥에 꽂을 수 있는 N개의 원판으로 이루어져 있습니다. 이 게임에서 다음의 규칙을 만족해야 합니다.
- 처음에 모든 원판은 A기둥에 꽂혀 있다.
- 모든 원판의 지름은 다르다.
- 이 원반은 세 개의 기둥 중 하나에 반드시 꽂혀야 한다.
- 작은 원반 위에 큰 원반을 놓을 수 없다.
- 한 번에 하나의 원판(가장 위에 있는 원판) 만을 옮길 수 있다.
- 이 규칙을 만족하며 A기둥에 있는 원반 N개를 모두 C 원반으로 옮기고 싶습니다.
모든 원반을 옮기기 위해 실행되어야 할 최소 원반 이동 횟수를 계산하는 프로그램을 완성해주세요.
- 즉, 세개의 기둥(A,B,C)가 있다고 가정할 때, A->C로 모든 원판을 옮겨야하고, 원판의 지름은 모두 다른데 작은 원판이 큰 원판보다 아래 머무르지 않게 하며 이동시키는 것
- 원판이 n개 일 때, 최소 이동 횟수 공식 :
(2**n) -1
- 시간복잡도 : O(2^n)
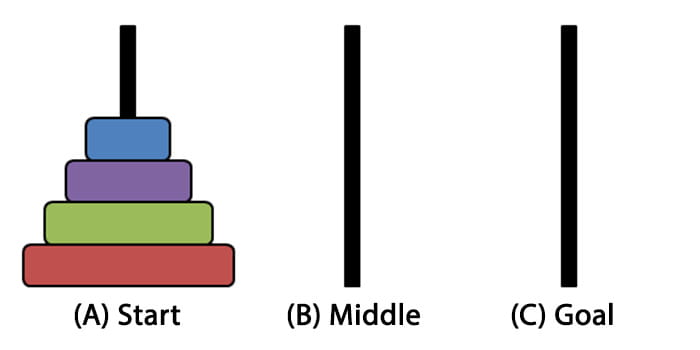
2. 하노이 탑 문제 과정
1. 원판이 1개 일 때(n=1),
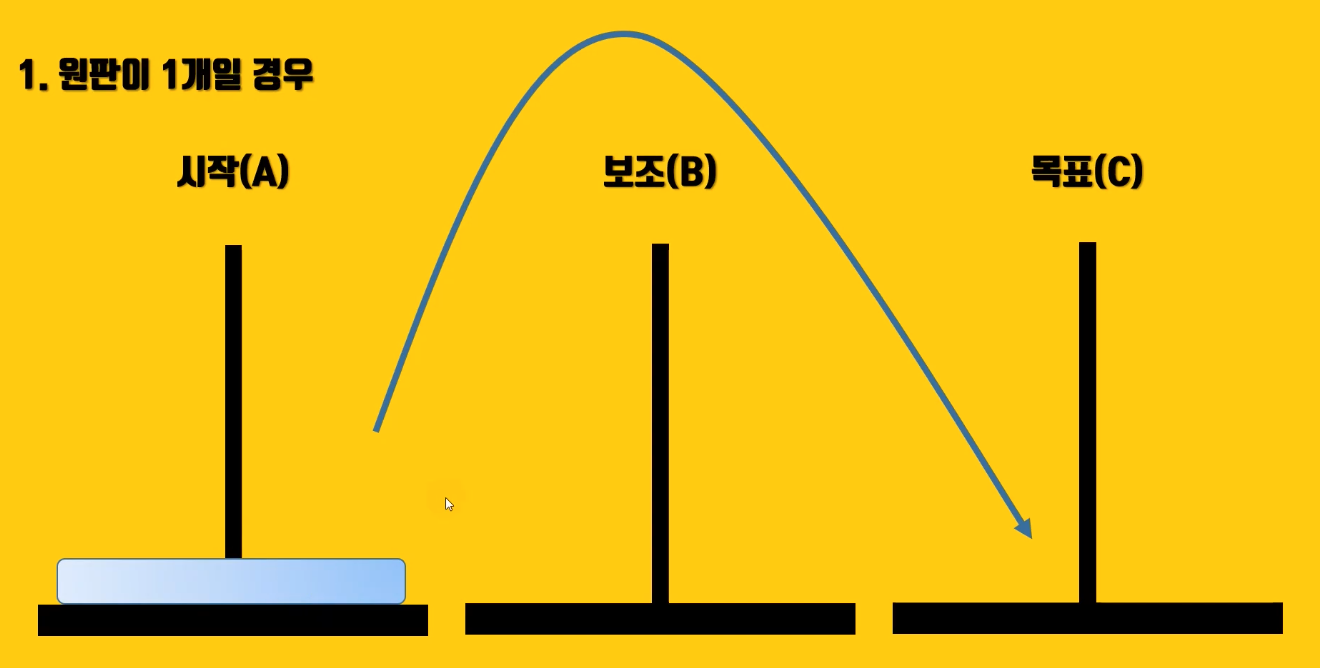
- 시작 기둥(A)에서 목표 기둥(C)로 바로 이동시키면 됨
- 이동 경로는 [A,C]이며, 이동 횟수는 1회임
res = []
def func(n, 첫기둥, 목표기둥, 중간기둥):
if n == 1:
res.append([첫기둥, 목표기둥])
return None
func(1, 'A', 'C', 'B')
- 함수호출 과정 : func(1, 'A', 'C', 'B')
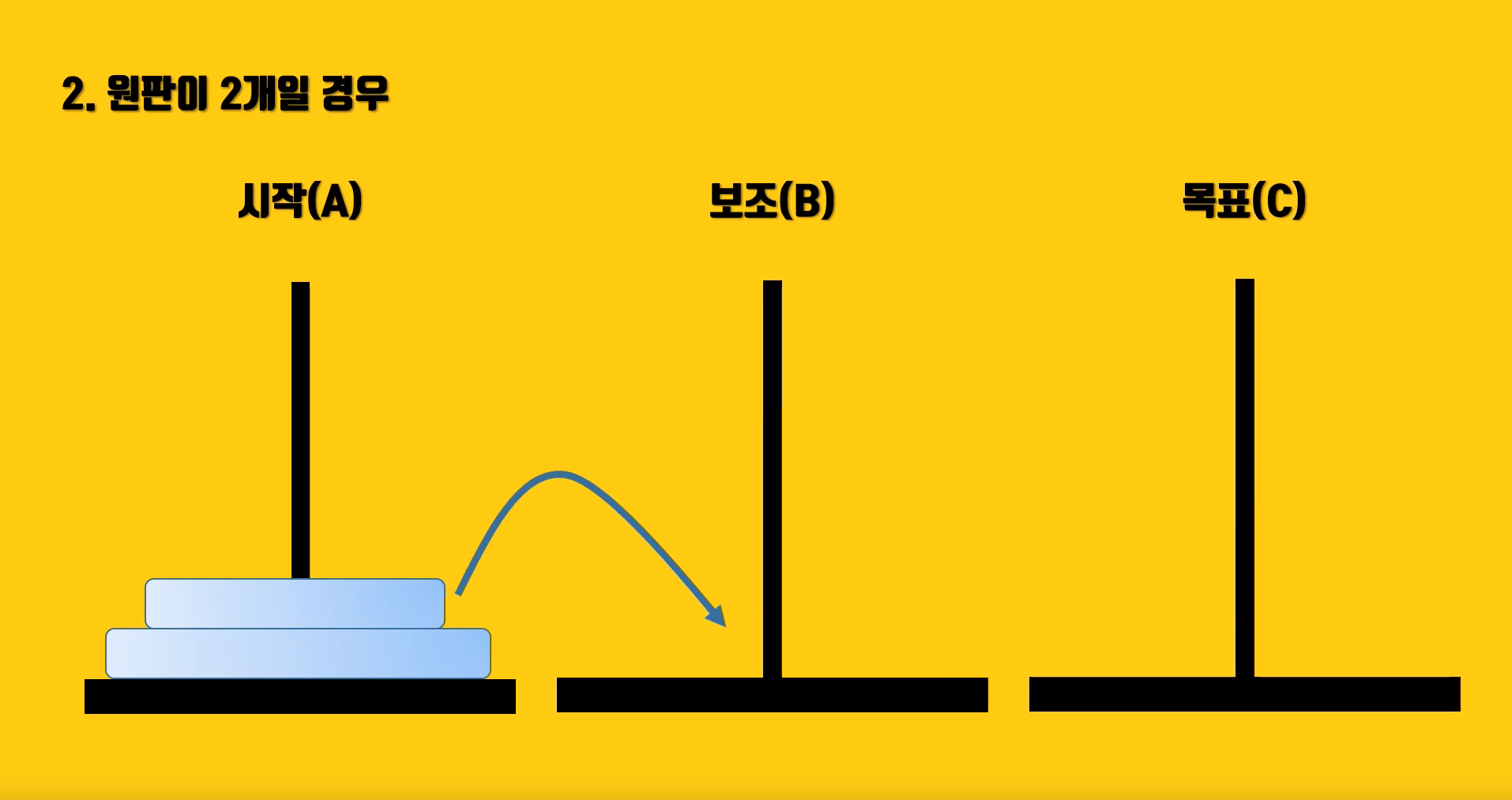
2. 원판이 2개 일 때(n=2),
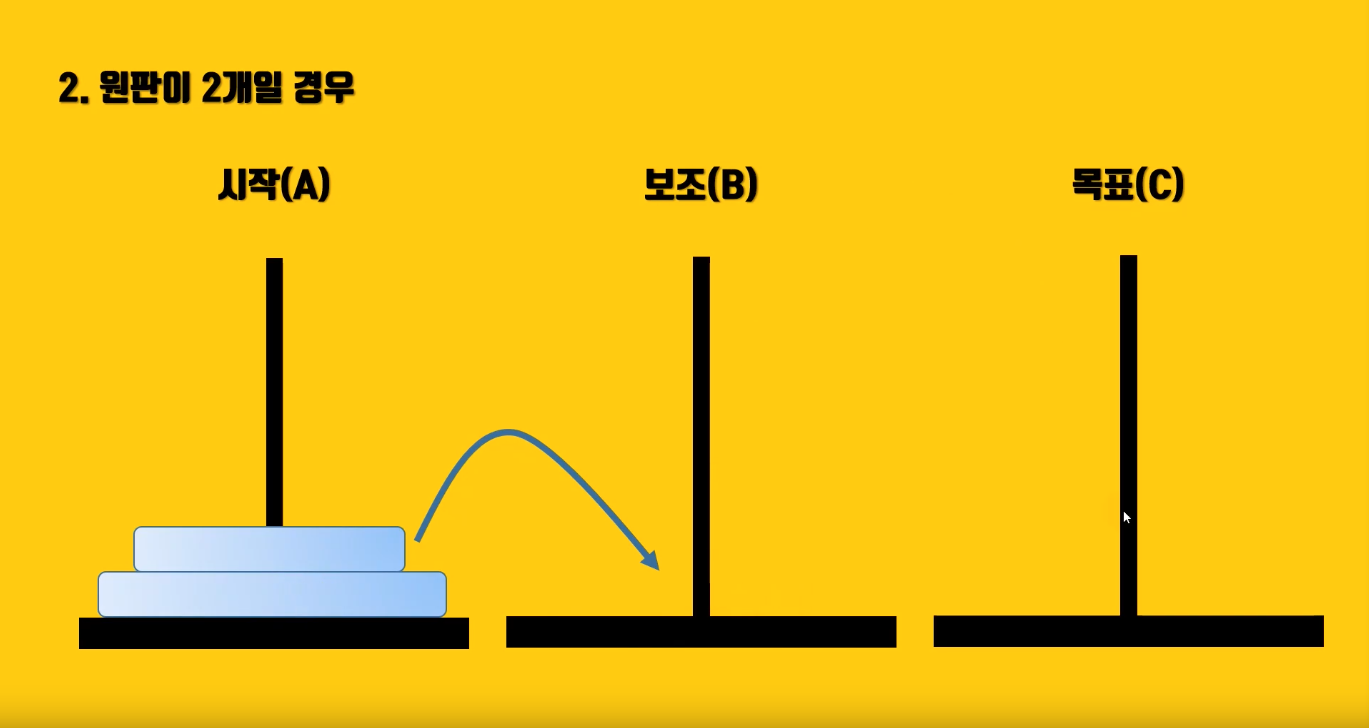
- 맨위에 있는 원판 1개를 시작기둥(A)에서 보조기둥(B)로 잠시 이동시킨 다음, 하나 남은 원판을 목표기둥(C)로 이동
- 원판이 2개 이상일 때에는 n-1개의 원판을 시작기둥(A)에서 중간기둥(B)로 옮김
- ⭐️ func(n, 첫기둥, 목표기둥, 중간기둥) → func(n-1, 첫기둥, 중간기둥, 목표기둥)
- 이후, 보조기둥(B)에 있는 원판 1개를 목표기둥(C)에 옮기면 A에서 C로 모두 이동됨
- 이동 경로는 [A,B] ⇢ [A,C] ⇢ [B,C] 이며, 이동 횟수는 3회임
res = []
def func(n, 첫기둥, 목표기둥, 중간기둥):
if n == 1:
res.append([첫기둥, 목표기둥])
return None
func(n-1, 첫기둥, 중간기둥, 목표기둥)
res.append([첫기둥, 목표기둥])
func(n-1, 중간기둥, 목표기둥, 첫기둥)
func(2, 'A', 'C', 'B')
- 함수호출 과정
- 시작 호출 : func(2, 'A', 'C', 'B')
- 첫번째 재귀식 호출 : func(1, 'A', 'B', 'C') 👈 [A-B] 출력 & return(종료)
- return 되었기 때문에 func(2, 'A', 'C', 'B')로 돌아옴
- res.append([첫기둥, 목표기둥]) 실행 👈 [A-C] 출력
- 두번째 재귀식 호출 : func(1, 'B', 'C', 'A') 👈 [B-C] 출력 & return(종료)
3. 원판이 3개 일 때(n=3),
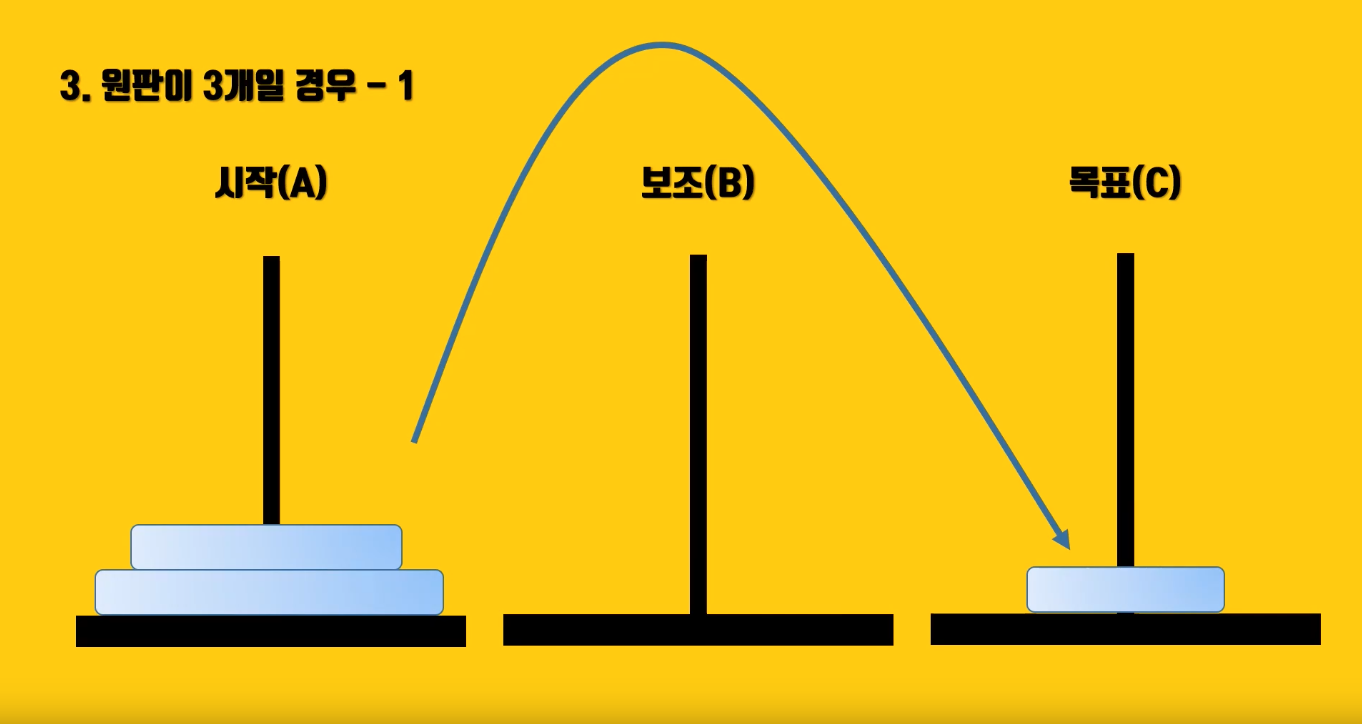
- 가장 작은(맨 위에 있는 원판) 1개를 시작기둥(A)에서 목표기둥(C)로 잠시 이동시킨 다음, 두번째로 작은(두번째 있던 원판)을 원판을 보조기둥(B)로 이동
- 목표기둥(C)에 있는 가장 작은 원판을 보조기둥(B)로 이동
- 원판이 2개 이상일 때에는 n-1개의 원판을 시작기둥(A)에서 중간기둥(B)로 옮김
- ⭐️ func(n, 첫기둥, 목표기둥, 중간기둥) → func(n-1, 첫기둥, 중간기둥, 목표기둥)
- 이후, 가장 큰 마지막 원판 1개를 목표기둥(C)에 옮기면 시작기둥(A)는 빈 상태
- ⭐️ res.append([첫기둥, 목표기둥])
- 이때, C에 가장 큰 원판이 이동되었기 때문에 C에 있는 원판 1개는 움직일리 없음
- ⭐️ 즉, C에 있는 원판을 버렸다고 쳤을 때, 보조기둥(B)와 시작기둥(A)를 swap하면 원판이 2개 있을 때 이동시키는 최초 상황과 같아짐
- ⭐️ func(n, 첫기둥, 목표기둥, 중간기둥) → func(n-1, 중간기둥, 목표기둥, 첫기둥)
- 보조기둥(B)에서 가장 작은 원판을 시작기둥(A)로 옮긴 뒤, 보조 기둥(B)에 있는 두번째로 작은 원판을 목표기둥(C)로 옮김
- 이동 경로는 [A,C] ⇢ [A,B] ⇢ [C,B] ⇢ [A,C] ⇢ [B,A] ⇢ [B,C] ⇢ [A,C]이며, 이동 횟수는 7회임
res = []
def func(n, 첫기둥, 목표기둥, 중간기둥):
if n == 1:
res.append([첫기둥, 목표기둥])
return None
func(n-1, 첫기둥, 중간기둥, 목표기둥)
res.append([첫기둥, 목표기둥])
func(n-1, 중간기둥, 목표기둥, 첫기둥)
func(3, 'A', 'C', 'B')
- 함수호출 과정
- 시작 호출 : func(3, 'A', 'C', 'B')
- 첫번째 재귀식 호출 : func(2, 'A', 'B', 'C') ⇢ func(1, 'A', 'C', 'B') 👈 [A-C] 출력 & return(종료)
- return 되었기 때문에 func(2, 'A', 'B', 'C')로 돌아옴
- res.append([첫기둥, 목표기둥]) 실행 👈 [A-B] 출력
- 두번째 재귀식 호출 : func(1, 'C', 'B', 'A') 👈 [C-B] 출력 & return(종료)
- return 되었기 대문에 func(3, 'A', 'C', 'B')로 돌아옴
- res.append([첫기둥, 목표기둥]) 실행 👈 [A-C] 출력(가장 아래 원판이 목표기둥(C)로 이동)
- 두번째 재귀식 호출 : func(2, 'B', 'C', 'A')
- 첫번째 재귀식 호출 : func(1, 'B', 'A', 'C') 👈 [B-A] 출력 & return(종료)
- return 되었기 대문에 func(2, 'B', 'C', 'A')로 돌아옴
- res.append([첫기둥, 목표기둥]) 실행 👈 [B-C] 출력(가운데 원판이 목표기둥(C)로 이동)
- 두번째 재귀식 호출 : func(1, 'A', 'C', 'B') 👈 [A-C] 출력 & return(종료)
3. 핵심 아이디어 정리
1) 원판이 1개일 때는 시작기둥(A)에서 목표 기둥(C)으로 옮김
- 원판이 1개일 때는 시작기둥(A)에서 목표기둥(C)로 이동하고, 이동했기 때문에 출력
- 또한 return 함으로써 현재 단계에서 탈출시켜 재귀호출를 진행시킴
res = []
def func(n, 시작기둥, 목표기둥, 보조기둥):
if n == 1:
res.append([시작기둥, 목표기둥])
return None
func(n-1, 시작기둥, 보조기둥, 목표기둥)
res.append([시작기둥, 목표기둥])
func(n-1, 보조기둥, 목표기둥, 시작기둥)
func(3, 'A', 'C', 'B')
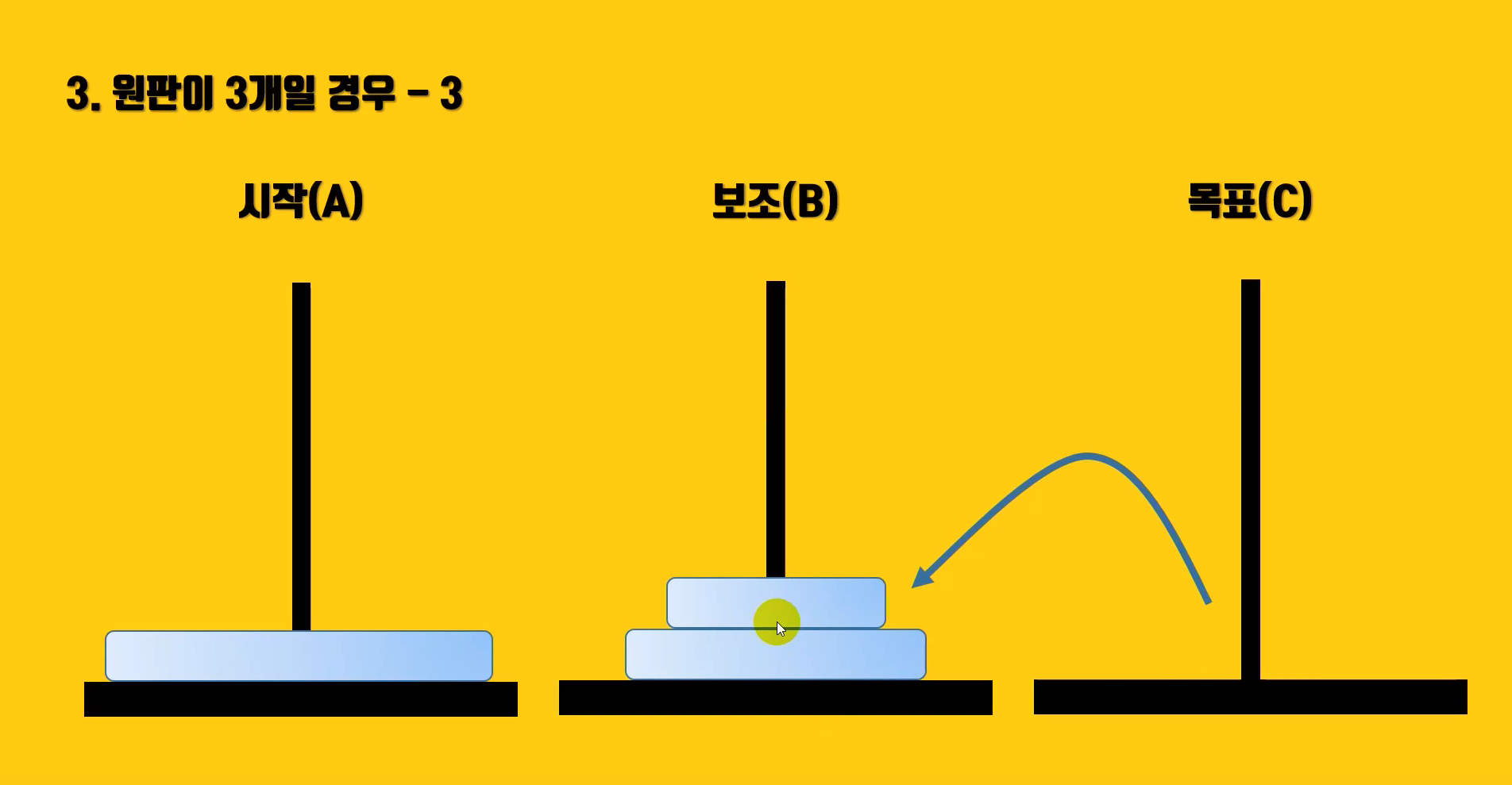
2) 원판 n-1개를 보조 기둥으로 이동
- 원판 n-1개를 보조 기둥으로 이동하기 때문에 func(n, 시작기둥, 목표기둥, 보조기둥)를 func(n-1, 시작기둥, 보조기둥, 목표기둥)로 순서를 바꿈
- 즉, 원판이 2개일 때는 원판 1개를 보조 기둥으로 옮기고, 원판이 3개일 때는 원판 2개를 보조 기둥으로 옮김
res = []
def func(n, 시작기둥, 목표기둥, 보조기둥):
if n == 1:
res.append([시작기둥, 목표기둥])
return None
func(n-1, 시작기둥, 보조기둥, 목표기둥)
res.append([시작기둥, 목표기둥])
func(n-1, 보조기둥, 목표기둥, 시작기둥)
func(3, 'A', 'C', 'B')
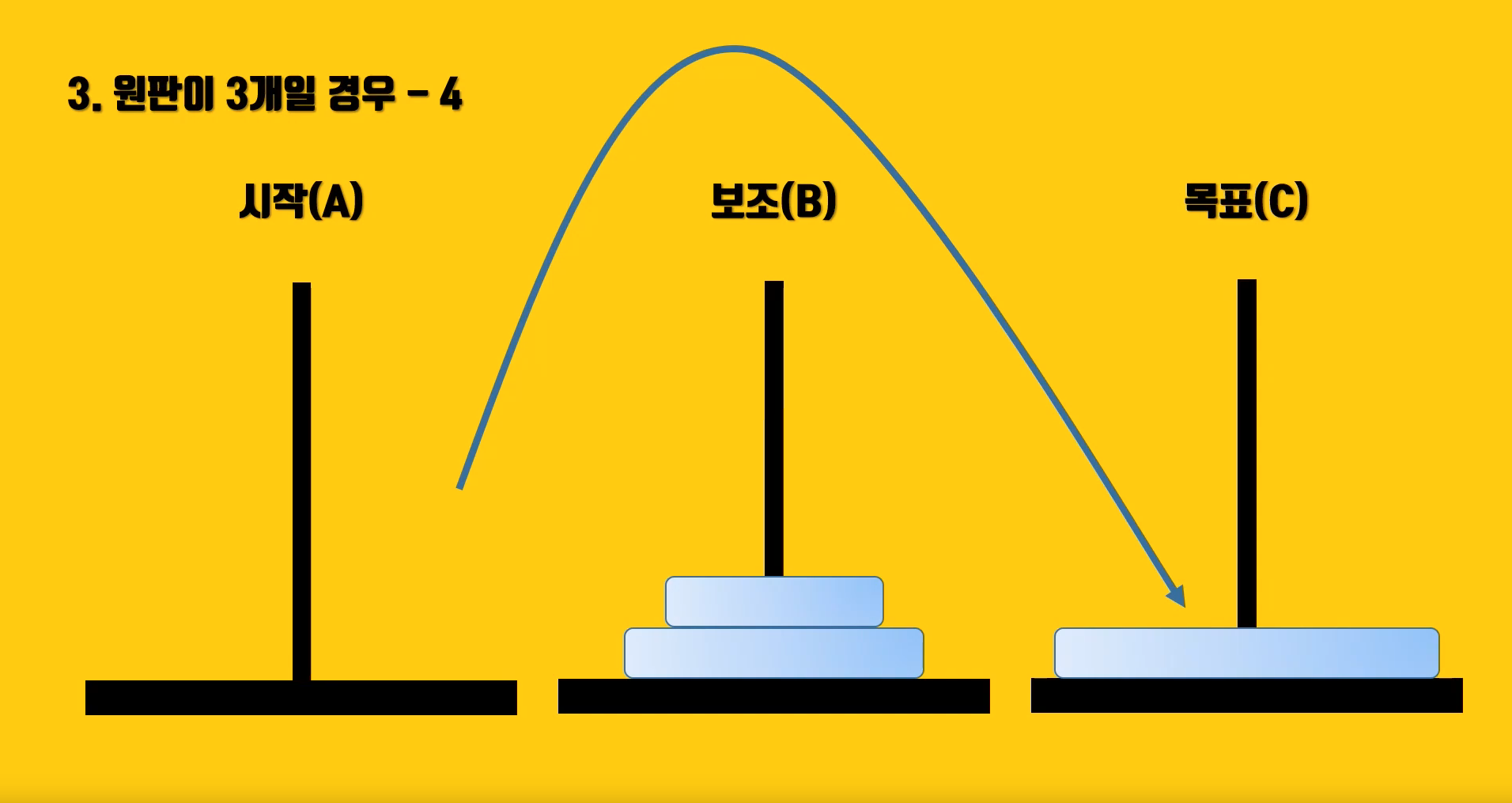
3) 가장 큰 원판을 목표 기둥(C)으로 이동
- n-1개를 보조기둥(B)로 옮겼다면, 다음 단계로 가장 큰 원판을 목표 기둥(C)로 이동
- 즉, 원판이 3개일 때 원판 2개를 보조기둥(B)로 모두 옮겼다면 시작기둥(A)에 남은 원판 1개를 목표기둥(C)로 이동
res = []
def func(n, 시작기둥, 목표기둥, 보조기둥):
if n == 1:
res.append([시작기둥, 목표기둥])
return None
func(n-1, 시작기둥, 보조기둥, 목표기둥)
res.append([시작기둥, 목표기둥])
func(n-1, 보조기둥, 목표기둥, 시작기둥)
func(3, 'A', 'C', 'B')
4) 보조기둥(B)와 시작기둥(A)를 swap
- 가장 큰 원판을 목표기둥(C)로 옮겼기 때문에 사실 이 원판은 이동할 일이 없어 영향을 미치지 않기 때문에 존재하지 않다고 생각해볼 수 있음
- 그럼 남은 원판으로 하노이의 탑 알고리즘을 시작하는 것과 같은 이동 횟수를 발생시킴
- 이에 보조기둥(B)에 남은 원판을 시작기둥(A)와 swap시켜 다시 시작하는 것과 마찬가지임
- 즉, 3개 원판으로 시작하였을 때, 2개의 원판을 보조기둥(B)로 이동시키고 시작기둥(A)에 남은 가장 큰 원판을 목표기둥(C)로 옮긴 것은 원판 2개로 하노이 탑을 하는 것과 같은 이동 횟수를 발생시킴
res = []
def func(n, 시작기둥, 목표기둥, 보조기둥):
if n == 1:
res.append([시작기둥, 목표기둥])
return None
func(n-1, 시작기둥, 보조기둥, 목표기둥)
res.append([시작기둥, 목표기둥])
func(n-1, 보조기둥, 목표기둥, 시작기둥)
func(3, 'A', 'C', 'B')
4. 재귀 호출 과정 요약
1) 원판이 3개일 때, 재귀 호출 과정 및 이동 경로 출력
- 7회 : [['A', 'C'], ['A', 'B'], ['C', 'B'], ['A', 'C'], ['B', 'A'], ['B', 'C'], ['A', 'C']]
f(n, 시작기둥, 목표기둥, 보조기둥)
res = []
def f(3, 'A', 'C', 'B'):
def f(2, 'A', 'B', 'C'):
def f(1, 'A', 'C', 'B'):
res.append(['A', 'C']) 🔥 n == 1일 때,
return None
res.append(['A', 'B']) 🔥 가장 큰 원판을 목표기둥으로 이동
def f(1, 'C', 'B', 'A'):
res.append(['C', 'B']) 🔥 n == 1일 때,
return None
res.append('A', 'C') 🔥 가장 큰 원판을 목표기둥으로 이동
def f(2, 'B', 'C', 'A'):
def f(1, 'B', 'A', 'C'):
res.append('B','A') 🔥 n == 1일 때,
return None
res.append('B', 'C') 🔥 가장 큰 원판을 목표기둥으로 이동
def f(1, 'A', 'C', 'B'):
res.append('A','C') 🔥 n == 1일 때,
return None
5. 하노의 탑 최종 코드
1) 최소 이동 경로
res = []
def hanoi(n, start, end, mid):
if n == 1:
res.append([start, end])
return None
hanoi(n-1, start, mid, end)
res.append([start, end])
hanoi(n-1, mid, end, start)
n = int(input())
hanoi(n, 'A', 'C', 'B')
print(res)
2) 최소 이동 횟수
res = 0
def hanoi(n, start, end, mid):
global res
if n == 1:
res += 1
return None
hanoi(n-1, start, mid, end)
res += 1
hanoi(n-1, mid, end, start)
n = int(input())
hanoi(n, 'A', 'C', 'B')
print(res)