알고리즘 기초 - 동적 계획법(Dynamic Programming)

🌈 동적 계획법(Dynamic Programming)

🔥 Dynamic Programming 란?

🔥 DP 예제 풀어보기

1. Dynamic Programming 란?

• Dynamic Programming은 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법
• DP 문제는 현재 상태가 어디서 오는지 관찰해야 하고, 최소, 최대, 경우의 수 문제는 DP 문제일 확률이 높음

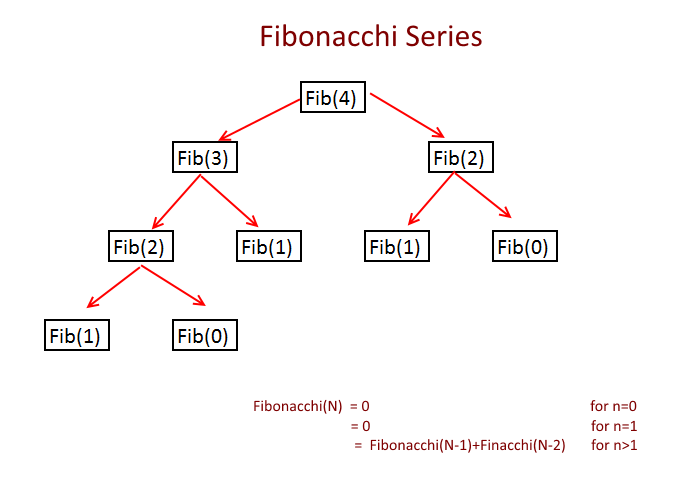
1) 피보나치 수열 문제

• n번째 피보나치를 수하는 문제를 재귀함수로 풀었을 때, 시간복잡도는 O(2^N) 이기 때문에 N에 30정도만 넣어도 10초가 소요됨
• 이 방법은 중복이 많아 시간 복잡도가 크다는 문제점을 가짐

def f(n):
  if n <= 1:
    return 1
  return f(n-1) + f(n-2)
print(f(4)) # 3
# f(4)
# => f(3) + f(2)
# => f(2) + f(1) + f(1) + f(0)
# => f(1) + f(0) + f(1) + f(1) + f(0)  

2) DP문제 푸는 방법

1) DP식 정의 : d[i] = i번째 피보나치 수
2) DP식 세우기 : d[i] = d[i-1] + d[i-2]
3) DP식 초기화 : d[0] = d[1] = 1

• 중복의 문제를 해결하기 위해서는 중복된 값을 여러번 계산하지 않도록 값을 기억해둘 수 있고, 이를 Memoization 이라함
• d라는 배열에 index값은 n번째 피보나치수와 같기 때문에 d 배열에서 n번째 피보나치수를 요청할 때 꺼내오기만하면 됨
• O(n)의 시간 복잡도를 가지지만, DP식을 세우기 어렵다는 단점이 있음

def f(n):
    d = [0 for i in range(n+1)] # 👈 Memoization
    d[0] = 0
    d[1] = 1
    for i in range(2, n+1):
        d[i] = d[i-1] + d[i-2]
    return d[n]
print(f(4)) # 3

2. DP 예제 풀어보기

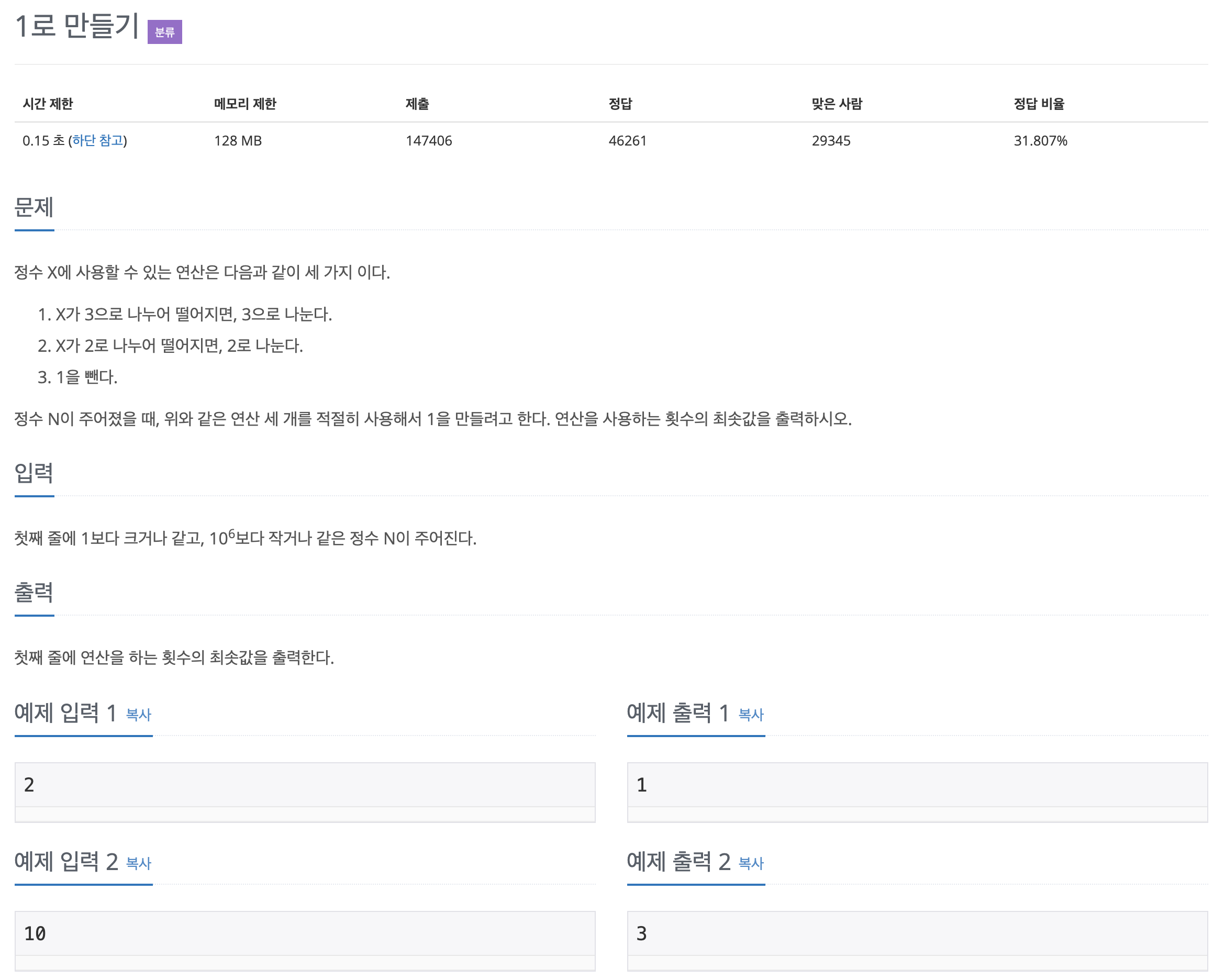
1) BOJ #1463 : 1로 만들기(https://www.acmicpc.net/problem/1463)

• 10부터 0까지 한자리씩 내려가면서 도달할 수 있는 최소 연산횟수 구해보기
  • 10 ⇢ 9 로 이동하는 최소 연산 횟수 : 1회(10-1)
  • 10 ⇢ 8 로 이동하는 최소 연산 횟수 : 2회(10-1-1)
  • 10 ⇢ 7 로 이동하는 최소 연산 횟수 : 3회(10-1-1-1)
  • 10 ⇢ 6 로 이동하는 최소 연산 횟수 : 4회(10-1-1-1-1)
  • 10 ⇢ 5 로 이동하는 최소 연산 횟수 : 1회(10%2)
  • 10 ⇢ 4 로 이동하는 최소 연산 횟수 : 2회(10%2-1)
  • 10 ⇢ 3 로 이동하는 최소 연산 횟수 : 2회((10-1)%3)
  • 10 ⇢ 2 로 이동하는 최소 연산 횟수 : 3회(((10-1)%3)-1) % 3회(((10%2)-1)%2)
  • 10 ⇢ 1 로 이동하는 최소 연산 횟수 : 3회(((10-1)%3)%3)
• 즉, 10을 기준으로 각 수에 도달할 수 있는 최소 횟수는 0 ⇢ 1 ⇢ 2 ⇢ 3 ⇢ 4 ⇢ 1 ⇢ 2 ⇢ 2 ⇢ 3 ⇢ 3
  
• DP식 정의하기
  • DP식 정의 : d[i] = i로 만드는데 드는 최소 연산 횟수
  • DP식 세우기 : d[i] = min(d[i*3], d[i*2], d[i+1]) + 1
  • DP식 초기화 : d[all] = inf, d[n] = 0

"""
1) DP식 정의 : d[i] = i로 만드는데 드는 최소 연산 횟수
2) DP식 세우기 : d[i] = min(d[i * 3], d[i * 2], d[i + 1]) + 1
3) DP식 초기화 : d[all] = inf, d[n] = 0
"""
# BOJ 1463번
import sys
n = int(sys.stdin.readline())
inf = 99999999
d = [ inf for i in range(3 * n + 1) ]
d[n] = 0
for i in range(n-1, 0, -1): # n이 10이라면, 9,8,7....1까지 순회
    d[i] = min(d[i * 3], d[i * 2], d[i + 1]) + 1
print(d[1])
"""
i = 10, = 0
i = 9, min(d[27], d[18], d[10]) + 1 => min(99999999,99999999,0) + 1 = 1
i = 8, min(d[24], d[16], d[9]) + 1 => min(99999999,99999999,1) + 1 = 2
i = 7, min(d[21], d[14], d[8]) + 1 => min(99999999,99999999,2) + 1 = 3
i = 6, min(d[18], d[12], d[7]) + 1 => min(99999999,99999999,3) + 1 = 4
i = 5, min(d[15], d[10], d[6]) + 1 => min(99999999,0,4) + 1 = 1
i = 4, min(d[12], d[8], d[5]) + 1 => min(99999999,2,1) + 1 = 2
i = 3, min(d[9], d[6], d[4]) + 1 => min(1,4,2) + 1 = 2
i = 2, min(d[6], d[4], d[3]) + 1 => min(4,2,2) + 1 = 3
i = 1, min(d[3], d[2], d[2]) + 1 => min(2,3,3) + 1 = 3
d = [99999999, 3, 3, 2, 2, 1, 4, 3, 2, 1, 0]
"""

2) BOJ # 1149 RGB거리(https://www.acmicpc.net/problem/1149)

• DP식 세우기
  1) DP식 정의 : d[i][j] = i번째 집을 j색으로 칠하는데까지 드는 최소 비용
  2) DP식 세우기
  - d[i][0] = min(d[i-1][1], d[i-1][2]) + colors[i][0]
  - d[i][1] = min(d[i-1][0], d[i-1][2]) + colors[i][1]
  - d[i][2] = min(d[i-1][0], d[i-1][1]) + colors[i][2]
  3) DP식 초기화 : d[0][0] = colors[0], d[0][1] = colors[1], d[0][2] = colors[2]
• d[i][0] 의 의미는 i번째 집을 0번 colors로 칠한다는 의미
• 즉, d[i][0]는 d[i-1][1], d[i-1][2]의 최소 비용에 colors[i][0]을 한 값임

"""
DP식 정의 : d[i][j] = i번째 집을 j색으로 칠하는데까지 드는 최소 비용
DP식 세우기
- d[i][0] = min(d[i-1][1], d[i-1][2]) + colors[i][0]
- d[i][1] = min(d[i-1][0], d[i-1][2]) + colors[i][1]
- d[i][2] = min(d[i-1][0], d[i-1][1]) + colors[i][2]
DP식 초기화 : d[0][0] = colors[0], d[0][1] = colors[1], d[0][2] = colors[2]
입력
26 40 83
49 60 57
13 89 99
colors = [
    [26, 40, 83], # <= 첫번째 집 RGB 
    [49, 60, 57], # <= 두번째 집 RGB
    [13, 89, 99]  # <= 세번째 집 RGB
]
d = [ [99999999,99999999,99999999], [99999999,99999999,99999999], [99999999,99999999,99999999] ]
"""
# BOJ 1149번
inf = 99999999
import sys
n = int(sys.stdin.readline())
colors = []
d = [] 
for i in range(n):
    r, g, b, = list(map(int, sys.stdin.readline().split()))
    colors.append([r,g,b])
    d.append([inf, inf, inf]) # i번째 집을 j색으로 칠하는데까지 드는 비용의 누적값
d[0][0] = colors[0][0] # 첫번째(0번째) 집까지 0번째색(빨강색)으로 칠하는데 드는 비용
d[0][1] = colors[0][1] # 첫번째(0번째) 집까지 1번째색(초록색)으로 칠하는데 드는 비용
d[0][2] = colors[0][2] # 첫번째(0번째) 집까지 2번째색(파랑색)으로 칠하는데 드는 비용
for i in range(1,n):
# 현재 집까지 칠하는데 까지의 최소 비용 = 이전 집까지 칠하는데 최소비용 + 현재 집 비용
# 이전 집까지 칠하는데 비용을 2개만 비교하는 이유는, 현재집과 색이 달라야하기 때문
    d[i][0] = min(d[i-1][1], d[i-1][2]) + colors[i][0] 
    d[i][1] = min(d[i-1][0], d[i-1][2]) + colors[i][1]
    d[i][2] = min(d[i-1][0], d[i-1][1]) + colors[i][2]
ans = min(d[n-1][0],d[n-1][1],d[n-1][2])
print(ans)
# print(d) # [[26, 40, 83], [89, 86, 83], [96, 172, 185]]
# print(colors) # [[26, 40, 83], [49, 60, 57], [13, 89, 99]]
"""
colors = [[26, 40, 83], [49, 60, 57], [13, 89, 99]]
d = [ [26,40,83], [99999999,99999999,99999999], [99999999,99999999,99999999] ]
n = 3, i = 1 일 때,
d[1][0] = min(d[0][1], d[0][2]) + colors[1][0] => min(40, 83) + 49 = 89
d[1][1] = min(d[0][0], d[0][2]) + colors[1][1] => min(26, 83) + 60 = 86
d[1][2] = min(d[0][0], d[0][1]) + colors[1][2] => min(26, 40) + 57 = 83
n = 3, i = 2 일 때,
d[2][0] = min(d[1][1], d[1][2]) + colors[2][0] => min(86, 83) + 13 = 96
d[2][1] = min(d[1][0], d[1][2]) + colors[2][1] => min(89, 83) + 89 = 172
d[2][2] = min(d[1][0], d[1][1]) + colors[2][2] => min(89, 86) + 99 = 185
ans = min(d[2][0],d[2][1],d[2][2]) => min(96, 172, 185) => 96
"""    

2) BOJ # 2579 계단오르기(https://www.acmicpc.net/problem/2579)

• DP식 정의 : d[i] = i위치까지 오면서 얻은 최대 점수
• DP식 세우기 : d[i] = max(d[i-2], d[i-3]+score[i-1])) + socre[i]
• DP식 초기화 : d[0] = score[0] // d[1] = score[0] + score[1] // d[2] = score[2] + max(score[0], score[1])

import sys
n = int(sys.stdin.readline())
score = [] # 각 계단을 밟을 때 점수
for i in range(n):
    score.append(int(sys.stdin.readline()))
d = [0 for i in range(n)] # i번째 계단까지 오르는데 최대 점수
d[0] = score[0] 
d[1] = score[0] + score[1]
d[2] = score[2] + max(score[0], score[1])
for i in range(3,n):
    d[i] = max(d[i-2], d[i-3]+score[i-1]) + score[i]
print(d[n-1])

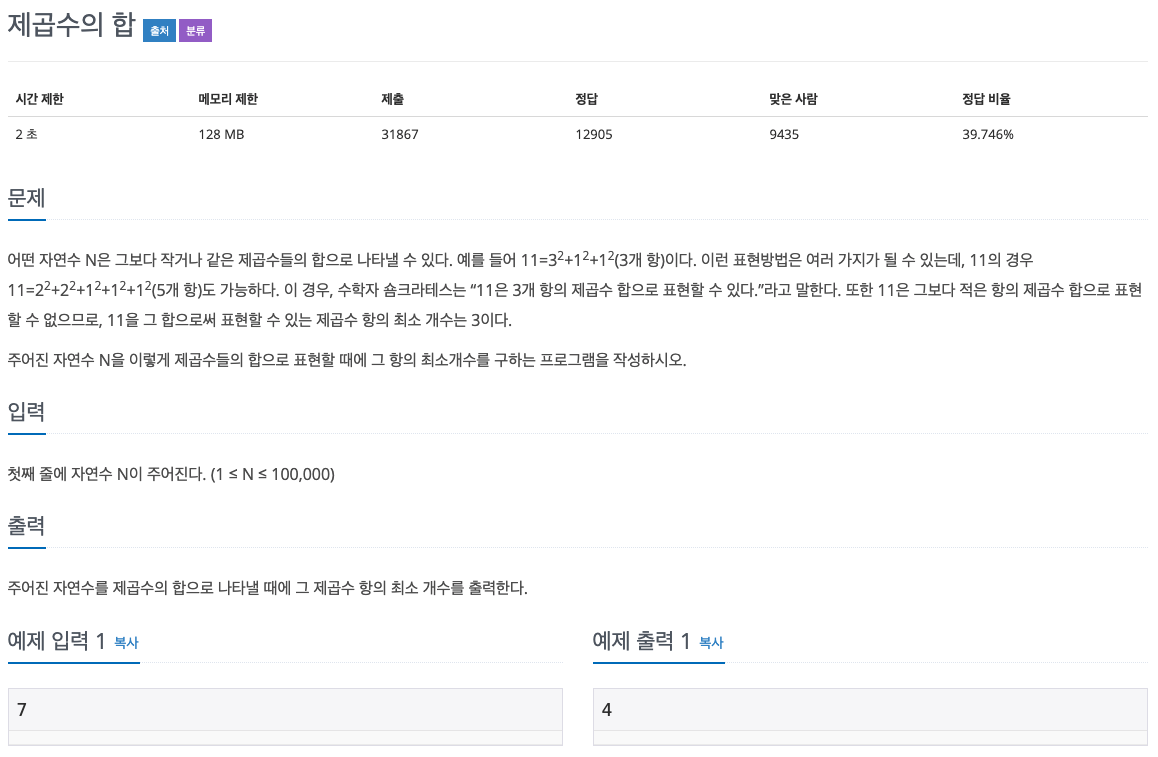
3) BOJ # 1699 제곱수의 합(https://www.acmicpc.net/problem/1699)

• DP식 정의 : d[i] = i수를 제곱수로 표현할 때 그 항의 최소 개수
• DP식 세우기 : d[i] = min(d[i], d[i-j*j]+1)
• DP식 초기화 : d[i] = i

import sys
n = int(sys.stdin.readline()) # 11
d = [i for i in range(n+1)]
# print(d) # # [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
for i in range(2, n+1): # 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
    for j in range(2, i+1): 
        if i < j*j:
            continue
        d[i] = min(d[i], d[i-j*j] + 1)
print(d[n])
"""
i = 2,  j = 2
i = 3,  j = 2,3
i = 4,  j = 2,3,4
i = 5,  j = 2,3,4,5
i = 6,  j = 2,3,4,5,6
i = 7,  j = 2,3,4,5,6,7
i = 8,  j = 2,3,4,5,6,7,8
i = 9,  j = 2,3,4,5,6,7,8,9
i = 10, j = 2,3,4,5,6,7,8,9,10
i = 11, j = 2,3,4,5,6,7,8,9,10,11
"""