알고리즘 기초 - 선형 탐색(Sequential Search) & 이진 탐색(Binary Search)

🌈 선형 탐색 & 이진 탐색

🔥 탐색 알고리즘 이란?

🔥 선형 탐색(Sequential Search)

🔥 이진 탐색(Binary Search)

🔥 bisect 라이브러리

🔥 이진 탐색(Binary Search) 예제

1. 탐색 알고리즘 이란?

• 탐색은 어떤 조건을 만족하는 데이터를 찾아내는 알고리즘이며, 검색 알고리즘이라 부르기도 함
• 선형 탐색 : 리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 확인하는 방법
• 이진 탐색 : 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법

2. 선형 탐색(Sequential Search)

• 선형 탐색, 순차 탐색라고 부르고, 하나하나 순차적으로 일치하는지 검색을 진행
• 순차적으로 일치하는지 확인하는 경우의 수가 10의 8승(1억)이면 대략 1초 정도 소요됨

# Sequential Search 구현
def sequential_search(l, target):
    for i in range(len(l)):
        if l[i] == target:
            return True
    return False
# Sequential Search Test
import random
l = random.sample(range(50), 10) # [10, 4, 49, 2, 41, 16, 42, 38, 23, 3]
target = random.randint(0, 50) # 23
print(l, target)
print(sequential_search(l, target)) # True

• Sequential Search의 시간 복잡도는 O(N)
• Sequential Search으로 다양한 자료형 탐색하기

# 배열 내 검색을 진행하는 함수
def seq_search(a, key):
    for i in range(len(a)):
        if a[i] == key:
            return i
    return -1
# tuple, string, array
t = (4, 7, 5.6, 2, 3.14, 1)
s = 'string'
a = ['DTS', 'AAC', 'FLAC']
# (4, 7, 5.6, 2, 3.14, 1)에서 5.6의 인덱스는 2 입니다.
print(f'{t}에서 5.6의 인덱스는 {seq_search(t, 5.6)} 입니다.')
# string에서 n의 인덱스는 4 입니다. 
print(f'{s}에서 n의 인덱스는 {seq_search(s, "n")} 입니다. ')
# ['DTS', 'AAC', 'FLAC']에서 "DTS"의 인덱스는 0 입니다.
print(f'{a}에서 "DTS"의 인덱스는 {seq_search(a, "DTS")} 입니다.')

• 가로가 m, 세로가 n인 이중 리스트에서 k가 있는지 확인하는 선형탐색
• k가 존재하면 1, 존재하지 않으면 0을 출력

import sys
n, m, k = map(int, sys.stdin.readline().split())
ll = list()
for i in range(n):
    l = list(map(int, sys.stdin.readline().split()))
    ll.append(l)
res = False
for i in range(n):
    for j in range(m):
        if ll[i][j] == k:
            res = True
if res:
    print(1)
else:
    print(0)

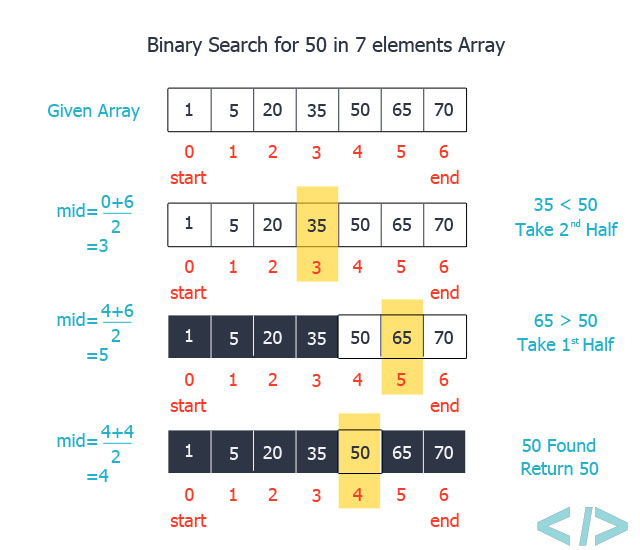
3. 이진 탐색(binary search)

1) binary search 반복문 구현

• 이진 탐색은 선형 탐색보다 빠르게 검색할 수 있다는 장점이 있음
• 다만, 이진 탐색 기법은 원소가 오름차순이나 내림차순으로 정렬된 배열일 경우에만 사용 가능
• 배열의 길이가 n일 때, 탐색 범위의 맨 앞의 인덱스는 left, 맨 끝을 right, 탐색 범위의 중앙을 mid라고하면, 탐색할 때 인덱스 값은 left은 0, right은 n-1, mid는 (n-1)//2의 값을 가짐
  

# Binary Search 구현(반복문)
def binary_search(l, target):
    left = 0
    right = len(l)-1
    while left <= right:
        mid = (left + right) // 2
        if l[mid] == target:
            return True
        elif l[mid] < target:
            left = mid + 1
        else : # elif l[mid] > target:
            right = mid - 1
    return False # 👈 while문 안에서 target을 찾지 못해, return을 만나지 못했을 경우
# Binary Search Test
import random
l = random.sample(range(50), 10) # [0, 18, 19, 23, 27, 28, 29, 36, 38, 46]
l.sort()
target = random.randint(0, 50) # 29
# print(l, target)
print(binary_search(l, target)) # True

2) binary search 재귀함수 구현

• 배열의 원소가 1개 뿐이고, 그것이 target과 일치하면 true를 반환
  • 🔍 if len(l) == 1 and target == l[0]: return True
• 배열의 원소가 1개 뿐이고, 그것이 target과 일치하지 않으면 False를 반환
  • 🔍 if len(l) == 1 and target != l[0]: return False
• 배열의 원소가 0이면 False 반환
  • 🔍 if len(l) == 0: return False
• 배열 길이를 2로 나눈 몫은 배열의 가운데 값
  • 🔍 mid = len(l) // 2

# Binary Search 재귀함수 구현
def binary_search(l, target): 
    # print(l) ## 👈 재귀함수에 전달된 배열을 출력
    if len(l) == 1 and target == l[0]: # l의 요소가 1개인데 그게 찾는 값일 때
        return True
    if len(l) == 1 and target != l[0]: # l의 요소가 1개인데 그게 찾는 값이 아닐 때
        return False
    if len(l) == 0:
        return False
    mid = len(l) // 2
    if target == l[mid]:
        return True
    else:
        if target > l[mid]:
            return binary_search(l[mid:], target)
        else:
            return binary_search(l[:mid], target)
# Binary Search Test
import random
l = random.sample(range(50), 10) # [1, 8, 14, 18, 26, 28, 30, 44, 46, 48] 
l.sort() # 정렬
target = random.randint(0, 50) # 18
# print(l, target) ## 👈 최초 함수에 전달되는 l과 target
print(binary_search(l, target)) # True

• Binary Search의 시간 복잡도는 O(logN)

4.bisect 라이브러리

• bisect_left([array],x) : 정렬된 순서를 유지하면서 배열(array)에 x를 삽입할 가장 왼쪽 인덱스 반환
• bisect_right([array],x) : 정렬된 순서를 유지하면서 배열(array)에 x를 삽입할 가장 오른쪽 인덱스 반환
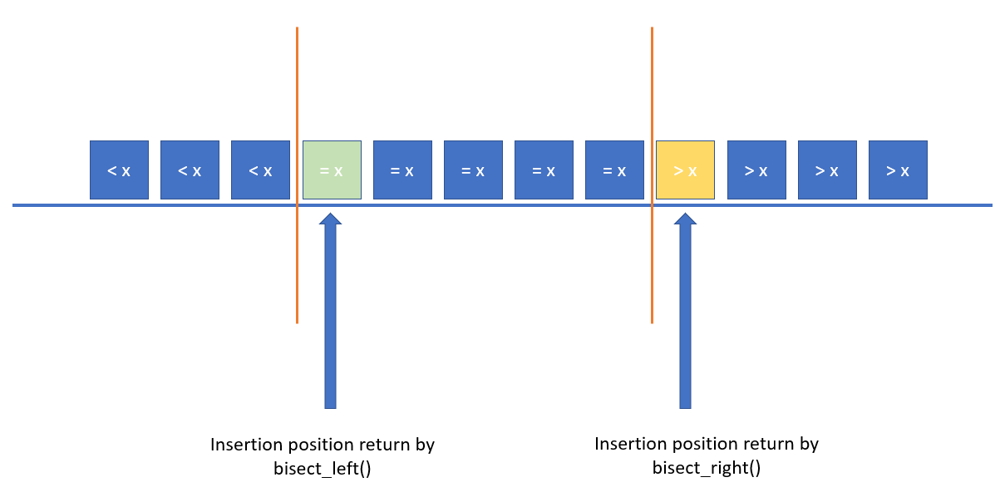
• bisect_left와 bisect_right의 값은 항상 같지 않음(x와 가장 가까운 값이 여러개 있을 수 있기 때문)

from bisect import bisect_left, bisect_right
import random
l = random.sample(range(50), 10)
x = random.randint(1,50)
l.sort()
print(l, x) # [2, 8, 11, 13, 14, 20, 41, 47, 48, 49] 36
print(bisect_left(l, x)) # 6
print(bisect_right(l, x)) # 6

• 특정 범위에 속하는 데이터 갯수 구하기

from bisect import bisect_left, bisect_right
def count_by_range(l, left_value, right_value):
    left_index = bisect_left(l, left_value)
    right_index = bisect_right(l, right_value)
    return right_index - left_index
l = [1,2,3,3,3,3,4,4,8,9]
# 값이 4인 데이터 갯수 출력
print(count_by_range(l, 4, 4)) # 2
# 값이 1에서 3 범위 안에 있는 데이터 갯수 출력
print(count_by_range(l, 1, 3)) # 6

5. 이진 탐색(Binary Search) 예제

1) 2차원 리스트에서 target을 찾으면 True, 찾을 수 없으면 False 반환

• m은 matrix의 세로 리스트 갯수이고, n은 matrix의 한 리스트의 가로 요소 갯수
• 최초 i는 0으로 시작해 첫번째 리스트의 마지막 요소인 j번째 요소를 target과 비교
• matrix[i][j] 가 target보다 크다면 j를 1개씩 줄여나가 왼쪽 요소를 탐색하고, matrix[i][j] 가 target보다 작다면, 다음 리스트로 넘어가기 위해 i를 1씩 더함

def searchMatrix(matrix, target):
    m = len(matrix)
    if m == 0:
        return False
    n = len(matrix[0])
    i = 0
    j = n - 1
    while i < m and  j >= 0:
        if matrix[i][j] == target:
            return True
        elif matrix[i][j] < target:
            i += 1
        else:
            j -= 1
    return False
# 입력2
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 3    
print('출력:' ,searchMatrix(matrix, target)) # 출력 : True
# 입력2
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 13
print('출력:' ,searchMatrix(matrix, target)) # 출력 : False