ANN을 이용한 벡터 유사도 검색

Yeonghwan·2025년 2월 2일

들어가며

다들 검색 기능을 구현해보신 경험이 있으신가요? 저는 SW 마에스트로 프로젝트 중에 AWS open search를 사용해보았는데요. 고사양 노드를 선택했다가 월 1,000 달러 정도의 비용이 청구되어 급하게 제거하고 JPA 기반 contains 방식으로 검색을 구현했던 경험이 있습니다.

그 때는 검색 알고리즘에 무엇이 있는지도 몰라서 일단 급하게 구현하기 바빴던 것 같은데요. 이번에는 대중적인 검색 알고리즘인 벡터 유사도 검색(Vector Similarity Search)을 구현해보고, 최적화를 진행해보려 합니다.

Elastic Search

먼저 검색 기능 중 가장 대중적인 오픈소스인 Elasticsearch의 검색 알고리즘에 대해 알아보겠습니다. 엘라스틱 서치는 Inverted Index를 이용하여 키워드(낱말)을 저장하며, 이러한 키워드들을 BM25라는 확률적 언어모델 방법을 이용하여 연관성을 랭킹하는 방식으로 검색합니다.

Inverted Index

Inverted Index(역색인)는 전통적인 텍스트 검색에서 사용하는 데이터 저장 방식으로, 문서 내에서 각 단어가 등장하는 위치를 저장하는 방식입니다. 아래와 같이 백과사진 마지막 페이지에 찾아보기로 단어들이 등장하는 경우가 좋은 예시입니다.

Tokenizer

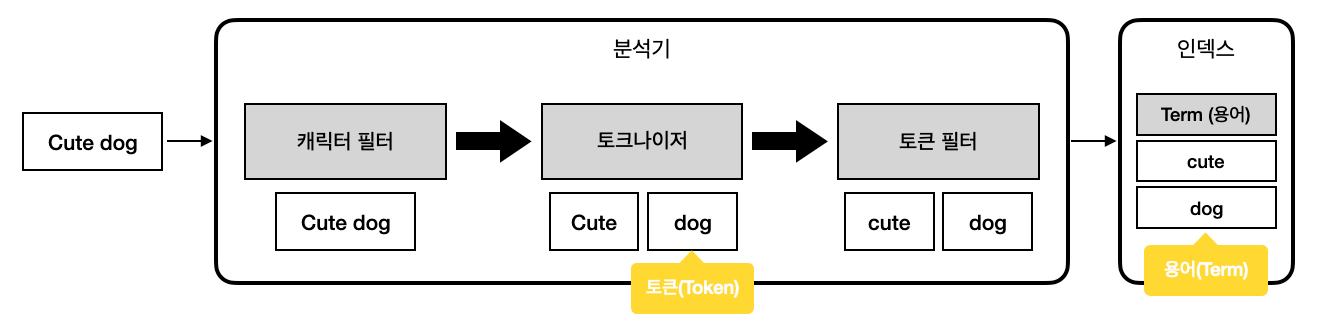
예를 들어 Cute dog 라는 string이 인덱스에 저장된다고 가정해보겠습니다. 먼저 캐릭터 필터에서 불필요한 문자를 제거합니다. 이 과정까지는 문자열 자체가 분리되지 않기 때문에 단순히 필터링 된 string 입니다.

이후 toknizer에서 필터리된 string을 자르는데, 이 때 잘린 단위를 Token 이라고 합니다.이런 토큰들은 이후 토큰 필터를 거쳐 한 번 더 정제되며, 최종적으로 인덱스에 저장됩니다.

Token은 분석기 내부에서 일시적으로 존재하는 상태이고, Term은 인덱싱 되어 있어 검색에 사용되는 최종적인 단위입니다.

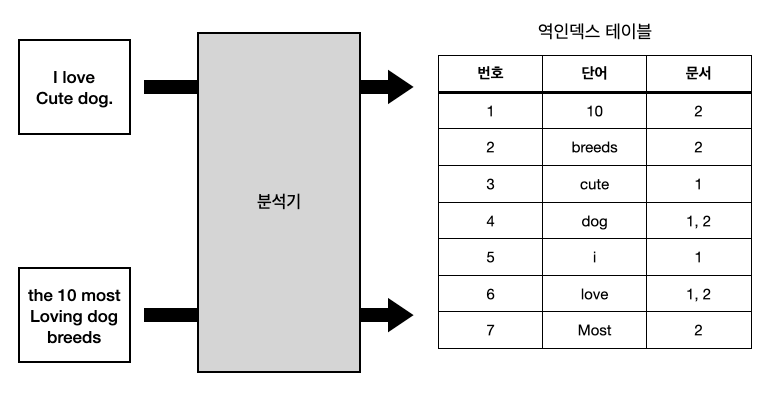
분석기는 정제를 마친 token을 인덱싱하는데, 이 때 앞서 말한 역인덱싱 방법으로 Term이 저장됩니다. 위 그림은 Elastic Search에서 Inverted Index를 만드는 예시입니다.

Limitation

Inverted Index를 활용한 방식은 빠른 검색 성능을 제공하며, 대용량 데이터에서도 효율적인 검색이 가능합니다.

하지만 정확한 keyword 검색 중심이기 때문에, 맥락을 고려한 유사도 검색에는 적합하지 않아 의미 기반 검색을 수행하기 어렵습니다.

Vector Similarity Search

Inverted Index를 이용한 전통적인 키워드 기반 검색의 단점을 해결하기 위한 방식으로는 벡터 유사도 검색 이 있습니다. 벡터 유사도 검색은 데이터를 고차원 벡터 공간에 매핑한 후, 유사한 데이터들을 찾는 방식입니다.

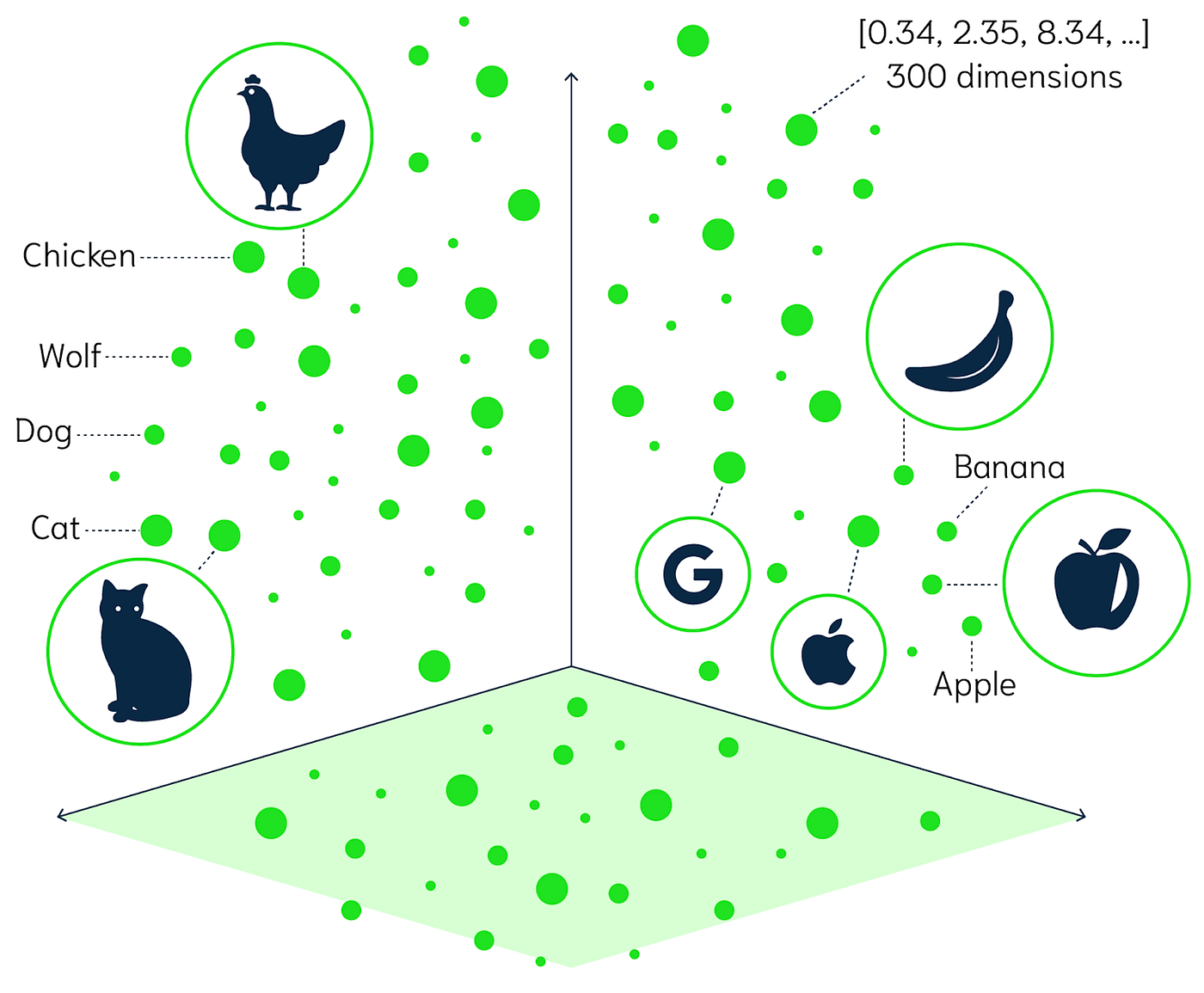
유사도 에 집중하는 특성 덕분에, feature vector 기반의 이미지 검색에 쓰이기도 하지만 이번에는 자연어 검색과 추천 시스템의 맥락에서 이를 소개해보려 합니다.

측정 방법

보통 벡터 유사도를 측정할 때는 코사인 유사도(Cosine similarity), 유클리드 거리(Euclidean Distance), 내적(Dot Product) 등의 전통적인 방법들이 사용되는데요.

이번에는 ANN(Approximate Nearest Neighbor)을 사용하여 신경망 자체에서 학습된 벡터를 비교하여 유사도를 계산해보려 합니다.

Nearest Neighbor

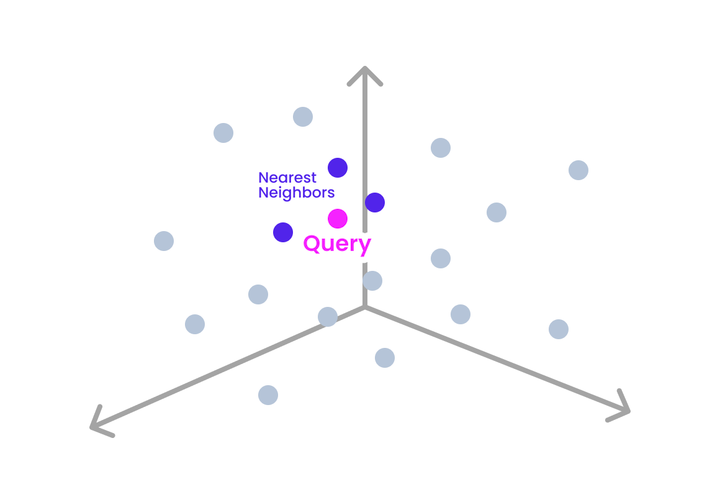
NN(Nearest Neighbor)은 Vector Space에서 내가 원하는 Quert Vector와 가장 유사한 Vector를 찾는 알고리즘입니다. RS(Recommendation System) 모델 서빙 자체는 Nearest Neighbor Search 와 굉장히 유사합니다. User Item Vector를 사용하여 주어진 Query Vector와 가장 유사한 벡터를 찾아주는 것이 추천 시스템이기 때문입니다.

NN의 가장 기본적인 방법은 Brute Force KNN으로 유사도를 정확하게 구하기 위해 모든 Vector와 유사도 비교를 수행하는 방법입니다.

당연히 dimension 개수에 비례한 cost가 필요하며, 직관적으로 완전 탐색은 대규모 데이터 환경에서 부적합하다는 판단이 가능합니다(AWS open search 기준 100차원 vector 100만개를 비교해도 46.3 시간이 걸린다고 합니다).

Approximate Nearest Neighbor

이를 해결하기 위해 정확도는 조금 포기하고 아주 빠른 속도로 주어진 vector의 근접이웃을 찾아야하는데, 이렇게 정확한 근접 이웃이 아닌 근사적으로 구한 근접이웃을 Approximate Nearest Neighbor라고 합니다.

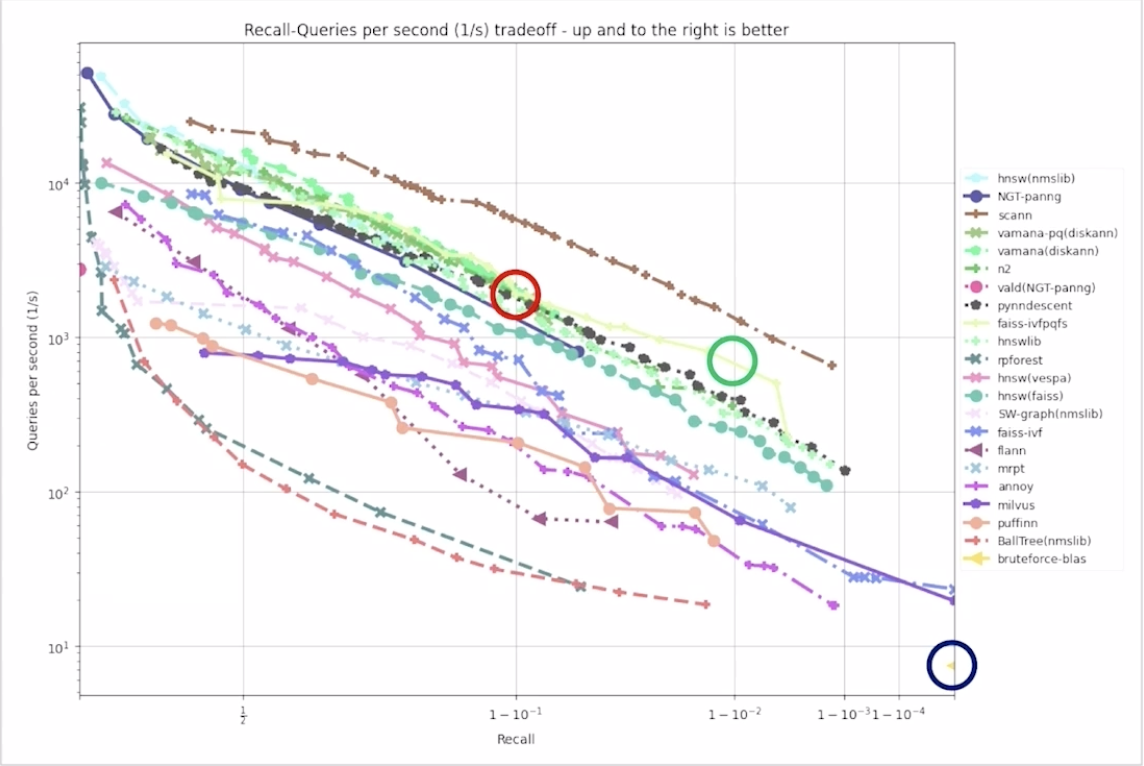
위 사진은 ANN 알고리즘의 성능을 나타낸 표인데요. x축(Recall)은 검색된 항목 중 관련 있는 항목의 비율을 나타냅니다. 리콜 값이 높을수록 시스템이 더 많은 관련 결과를 검색합니다.
y축(Queries per second (1/s))은 시스템이 초당 처리할 수 있는 쿼리 수를 나타내며, 값이 높을수록 시스템이 더 빠르게 쿼리를 처리함을 의미합니다.

측 우측 상단으로 향할수록 최적의 방법이며, 그래프를 보면 알 수 있듯, 좌측 상단과 우측 하단 사이의 선형적인 trade-off를 고려해야 함을 알 수 있습니다.

우측 하단 동그라미는 기존의 Brute Forece KNN으로 구한 값인데, 100%의 정확도인 대신에 초당 5개의 유사도를 비교할 수 있습니다.
중앙 빨간 동그라미는 ANN 기법으로 구한 값인데, 90%의 정확도를 가지고 초당 1,000개 이상의 유사도를 비교할 수 있습니다.
초록 동그라미는 다른 ANN 기법으로 구한 값인데, 99%의 정확도를 가지고 초당 7~800개의 유사도를 비교할 수 있습니다.

이처럼 실제 서빙시에는 근접 이웃의 정확도를 조금 포기하고 시간 및 비용을 크게 절감하는 선택을 할 수 있습니다.

구현

이제 간단하게 go lang을 이용하여 ANN 벡터 유사도 검색을 구현해보려 합니다. Go는 컴파일언어로, 실행속도와 메모리 관리 효율에서 이점이 있습니다. 한 번 사용해보고 싶었던 언어였는데, 대규모 벡터 데이터를 안정적으로 처리하는 것에 이점이 있다고 판단하여 이번에 도입해보려 합니다.

먼저 Brute Force KNN을 구현해보고, 이후 최적화를 통해 ANN으로 발전 시키는 과정을 소개해보려 합니다.

Brute Force KNN


// 벡터와 ID를 포함하는 구조체
type Vector struct {
    ID     int
    Values []float64
}

// 검색 결과를 저장하는 구조체
type SearchResult struct {
    ID        int
    Similarity float64
}

// 벡터 데이터베이스 구조체
type VectorDB struct {
    vectors []Vector
}

// 새로운 벡터 데이터베이스 생성
func NewVectorDB() *VectorDB {
    return &VectorDB{
        vectors: make([]Vector, 0),
    }
}

// 벡터 추가
func (db *VectorDB) AddVector(id int, values []float64) {
    db.vectors = append(db.vectors, Vector{
        ID:     id,
        Values: values,
    })
}

우선 위와 같이 구조체를 선언하고, 간단하게 벡터를 추가하는 함수를 만들어줍니다.

// 코사인 유사도 계산
func cosineSimilarity(a, b []float64) float64 {
    if len(a) != len(b) {
        return 0
    }
    
    var dotProduct, normA, normB float64
    for i := 0; i < len(a); i++ {
        dotProduct += a[i] * b[i]
        normA += a[i] * a[i]
        normB += b[i] * b[i]
    }
    
    if normA == 0 || normB == 0 {
        return 0
    }
    
    return dotProduct / (math.Sqrt(normA) * math.Sqrt(normB))
}

다음엔 앞서 말했던 코사인 유사도를 계산하는 함수를 정의합니다. 코사인 유사도는 두 벡터 간의 각도 차이를 나타내는 지표로, 두 벡터가 얼마나 비슷한지(유사한지)를 측정합니다.

// 가장 유사한 벡터 검색
func (db *VectorDB) Search(query []float64, topK int) []SearchResult {
    results := make([]SearchResult, 0)
    
    // 모든 벡터와의 유사도 계산
    for _, vec := range db.vectors {
        similarity := cosineSimilarity(query, vec.Values)
        results = append(results, SearchResult{
            ID:         vec.ID,
            Similarity: similarity,
        })
    }
    
    // 유사도 기준으로 정렬
    sort.Slice(results, func(i, j int) bool {
        return results[i].Similarity > results[j].Similarity
    })
    
    // topK 개수만큼 반환
    if len(results) > topK {
        results = results[:topK]
    }
    
    return results
}

func main() {
    // 벡터 데이터베이스 생성
    db := NewVectorDB()
    
    // 샘플 벡터 추가
    db.AddVector(1, []float64{1.0, 0.5, 0.3})
    db.AddVector(2, []float64{0.8, 0.2, 0.9})
    db.AddVector(3, []float64{0.1, 0.9, 0.4})
    
    // 검색 쿼리 벡터
    query := []float64{1.0, 0.5, 0.3}
    
    // 상위 2개 유사한 벡터 검색
    results := db.Search(query, 2)
    
    // 결과 출력
    for _, result := range results {
        fmt.Printf("ID: %d, Similarity: %.4f\n", result.ID, result.Similarity)
    }
}

이후 주어진 쿼리 벡터와 데이터베이스에 저장된 모든 벡터 간의 유사도를 계산하여, 가장 유사한 topK개의 벡터를 반환합니다.

먼저, 데이터베이스에 있는 각 벡터와 쿼리 벡터 간의 코사인 유사도를 계산하고, SearchResult에 ID와 Similarity를 저장합니다.
이후 유사도를 기준으로 내림차순 정렬하여, 가장 유사한 벡터들을 상위 topK개만 반환합니다.

최적화

이제 벡터 검색 성능을 향상시키기 위해 PCA와 LSH를 이용하여 최적화를 진행해보겠습니다.
먼저 데이터를 쇼핑몰로 가정하고, 아래와 같은 아이템을 넣어주었습니다.

    // 상품 데이터 추가
    // 벡터 의미: [가격대(0-1), 캐주얼스타일(0-1), 포멀스타일(0-1), 스포티스타일(0-1), 계절감(0-1)]
    db.AddProduct(Product{
        ID:          1,
        Name:        "캐주얼 티셔츠",
        Price:       29900,
        Vector:      []float64{0.3, 0.9, 0.1, 0.4, 0.7}, // 저가, 매우 캐주얼, 여름
        Category:    "의류",
        Description: "편안한 데일리 티셔츠",
    })

    db.AddProduct(Product{
        ID:          2,
        Name:        "정장 셔츠",
        Price:       89000,
        Vector:      []float64{0.7, 0.1, 0.9, 0.1, 0.5}, // 중가, 매우 포멀, 무난
        Category:    "의류",
        Description: "고급 비즈니스 셔츠",
    })

    db.AddProduct(Product{
        ID:          3,
        Name:        "운동용 반팔",
        Price:       39900,
        Vector:      []float64{0.4, 0.3, 0.1, 0.9, 0.8}, // 저가, 매우 스포티, 여름
        Category:    "의류",
        Description: "기능성 스포츠 웨어",
    })

    db.AddProduct(Product{
        ID:          4,
        Name:        "캐주얼 셔츠",
        Price:       49900,
        Vector:      []float64{0.5, 0.8, 0.3, 0.2, 0.6}, // 중가, 캐주얼, 무난
        Category:    "의류",
        Description: "데일리 캐주얼 셔츠",
    })

Principal Component Analysis

PCA(Principal Component Analysis)는 데이터의 차원을 줄여 벡터 검색 속도를 높이는 기법입니다.

먼저 PCA의 필요성에 대한 이해를 해볼까요. 아래와 같이 좌측의 2차원 데이터를 우측의 1차원 데이터로 바꾼다고 생각해봅시다.

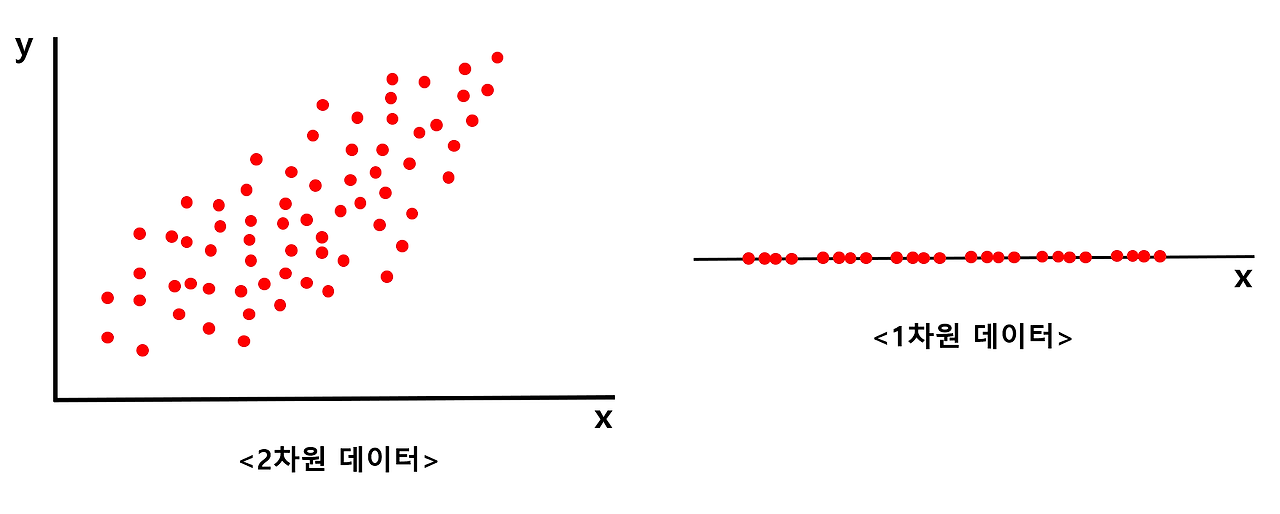
이 경우에 새로운 축을 x축, y축, y=x축 등 어디로 설정한다 하더라도 2차원 데이터의 특징을 모두 살리면서 1차원으로 표현할 수는 없을 것입니다. 이 때 최대한 특징을 살리면서 차원을 낮춰주는 방법 중 하나가 바로 PCA입니다.

키와 몸무게를 예시로 차원을 축소해볼까요?

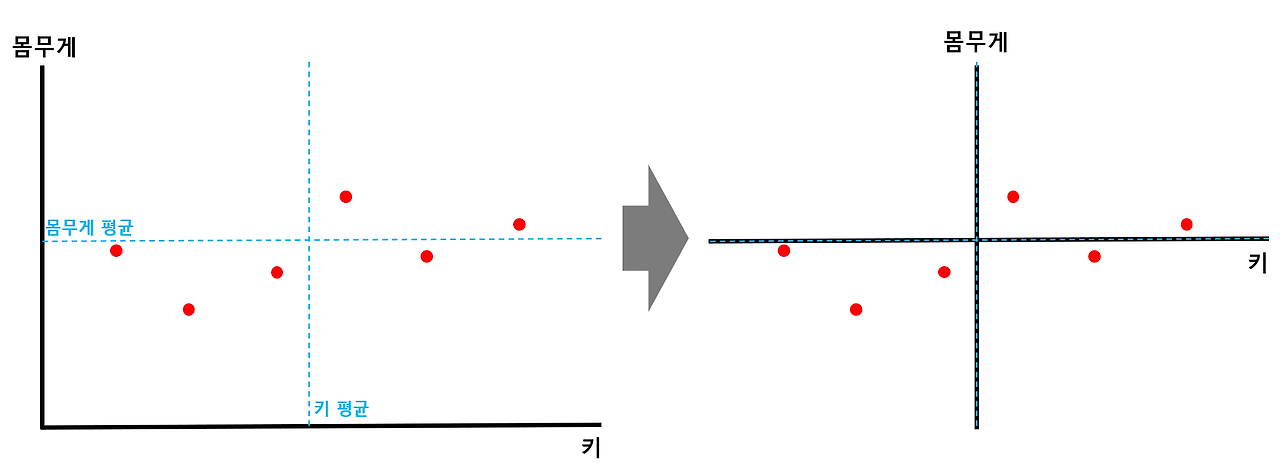
먼저 각 축의 평균값을 구해주고, 각 평균값 교차점을 원점이 되도록 전체 데이터를 shift 해줍니다.

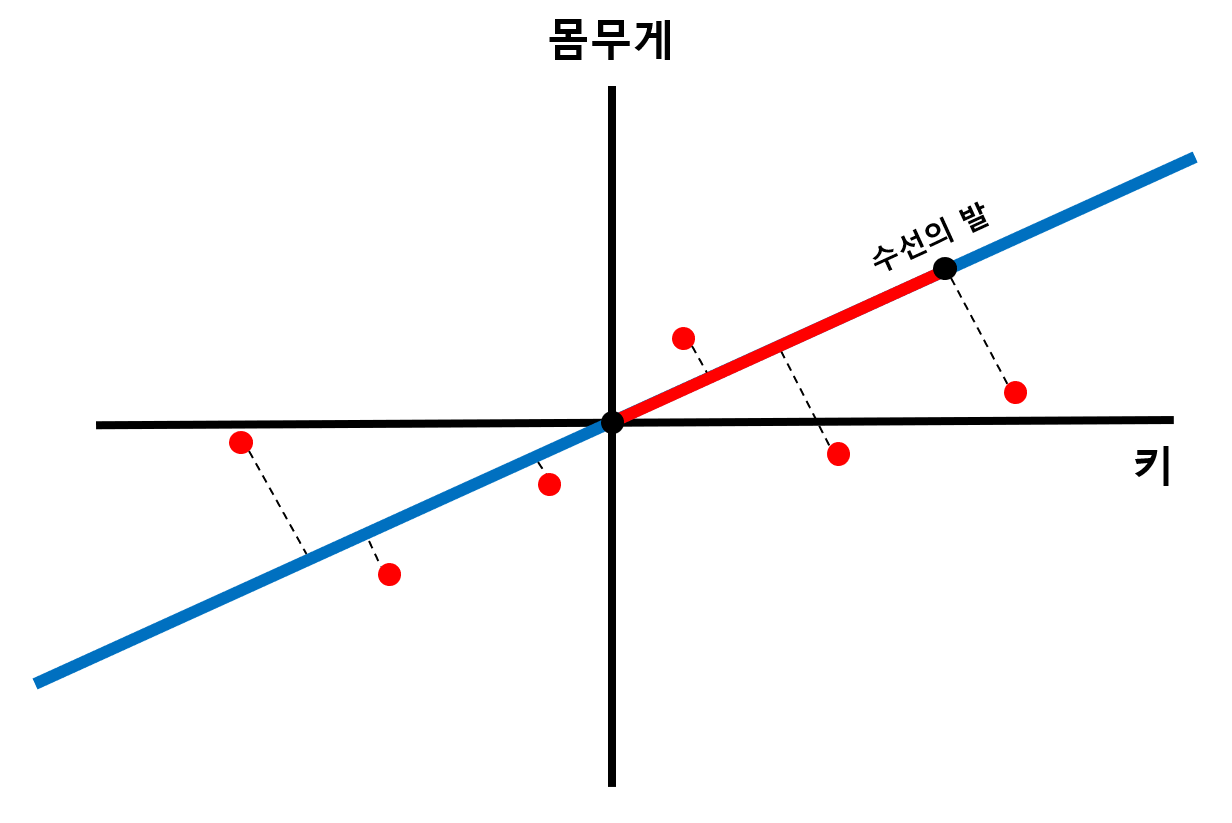
이후 데이터에서 원점을 지나는 직선에 수선의 발을 내려, 해당 길이가 최대가 되는 직선(빨간 선분)을 찾습니다. 이러면 각 데이터마다 각각의 빨간 선분을 가지게 될텐데, 이 선분들의 길이 제곱 합이 최대가 되는 직선을 찾습니다.

이 때 이 빨간 선들의 길이합을 SS(Sum of Squares) 라고 하겠습니다.

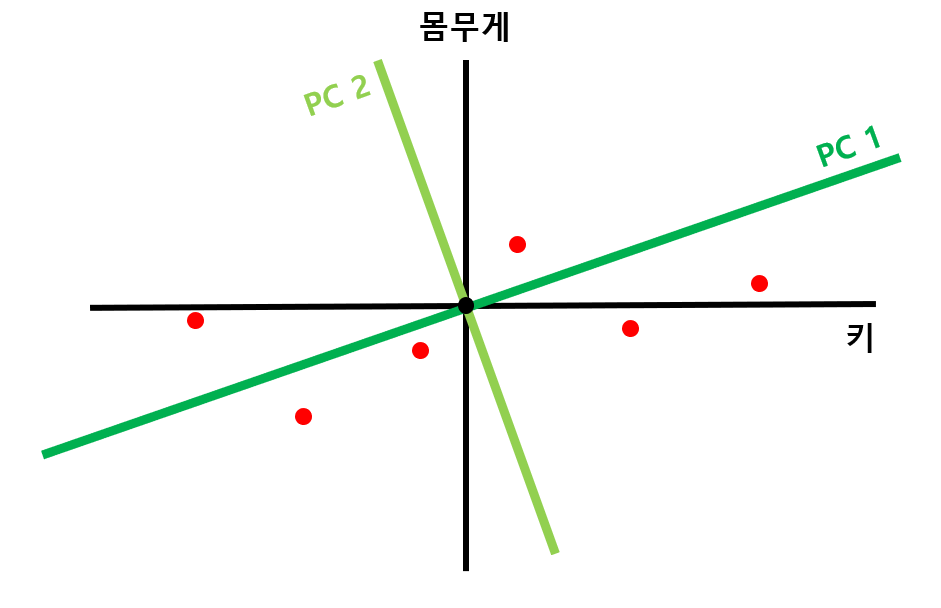
이렇게 찾은 직선을 PC1이라고 하고, 이와 직교하는 직선을 PC2라고 해보겠습니다. 차원이 n개라면 PCn까지 직선을 찾을 수 있겠죠?

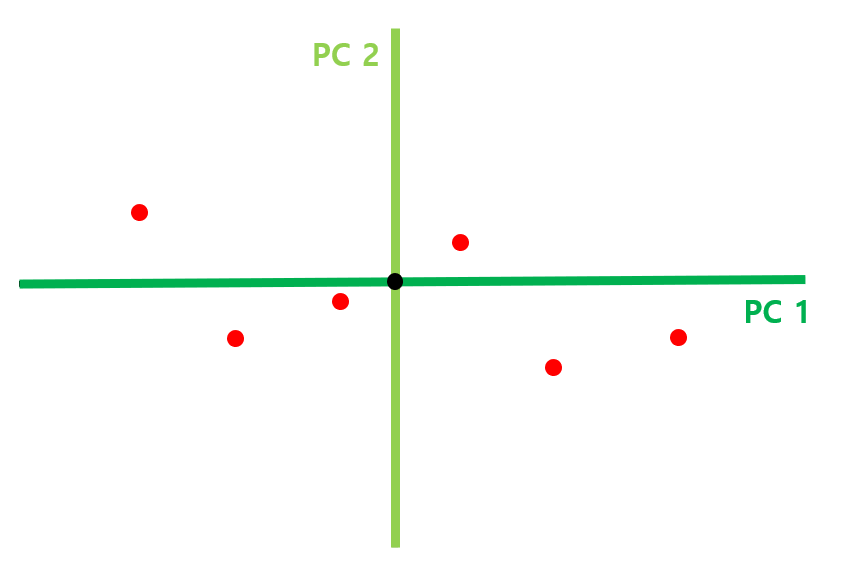
앞서 구한 PC1과 PC2 직선을 각각 x, y 축이 되도록 데이터를 회전시키면 위와 같은 그림이 되는데요. 이제 각 PC 축이 전체 데이터를 얼마나 잘 표현하고 있는지 보여주는 scree plot을 그려보겠습니다.

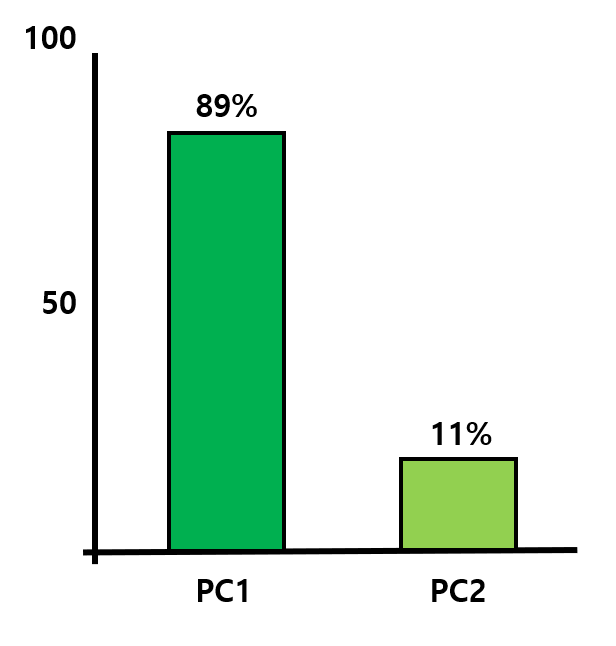
scree plot은 각 PC들의 SS 비율로 구분됩니다. 만약 PC1과 PC2의 비율이 8.9 : 1.1 이라면 위와 같이 scree plot을 그려줄 수 있겠네요.

여기서 "어떻게 특징을 살리며 차원을 낮출 수 있을까"의 물음에서 시작한 PCA의 목표를 고려하여 차원을 축소하면 됩니다. 만약 89%의 특징만으로 해당 데이터를 잘 나타낼 수 있을 것이라고 판단되면, PC2 축을 제거하고 PC1 축만을 가지고 1차원으로 나타낼 수 있습니다.

예를 들어 3차원 데이터가 PCA를 통해 PC 1~3의 3개 축을 잡았고, scree plot에서 PC 1~3이 각각 73 : 17 : 10 의 비율로 구성되어 있다고 가정해보겠습니다. 이러면 우리는 2가지 선택을 해볼 수 있겠네요.

데이터 특징을 90% 살리면서 3차원에서 2차원으로 차원을 축소
데이터 특징을 73% 살리면서 3차원에서 1차원으로 차원을 축소

이처럼 선택지는 다양해질 수 있으며, 차원의 수와 리소스를 고려하여 적합한 선택을 하면 됩니다.

PCA - Source Code

참고를 위해 아래 코드를 첨부합니다. 앞서 말씀드린 설명을 코드로 옮긴 것이니 참고로 보셔도 충분합니다.

func PCA(vectors [][]float64, targetDim int) [][]float64 {
	if len(vectors) == 0 || len(vectors[0]) == 0 || targetDim >= len(vectors[0]) {
		return vectors
	}

	// 1. 평균 계산
	dim := len(vectors[0])
	mean := make([]float64, dim)
	for _, v := range vectors {
		for j := range v {
			mean[j] += v[j]
		}
	}
	for j := range mean {
		mean[j] /= float64(len(vectors))
	}

	// 2. 중심화
	centered := make([][]float64, len(vectors))
	for i, v := range vectors {
		centered[i] = make([]float64, dim)
		for j := range v {
			centered[i][j] = v[j] - mean[j]
		}
	}

	// 3. 공분산 행렬 계산
	cov := make([][]float64, dim)
	for i := range cov {
		cov[i] = make([]float64, dim)
		for j := range cov[i] {
			for k := 0; k < len(vectors); k++ {
				cov[i][j] += centered[k][i] * centered[k][j]
			}
			cov[i][j] /= float64(len(vectors) - 1)
		}
	}

	// 4. 주성분 계산 (power iteration 방법)
	components := make([][]float64, targetDim)
	for i := range components {
		components[i] = make([]float64, dim)
		// 초기 벡터
		for j := range components[i] {
			components[i][j] = rand.Float64()
		}
		// Power iteration
		for iter := 0; iter < 100; iter++ {
			// 행렬-벡터 곱
			newVec := make([]float64, dim)
			for j := range newVec {
				for k := range cov[j] {
					newVec[j] += cov[j][k] * components[i][k]
				}
			}
			// 정규화
			norm := 0.0
			for j := range newVec {
				norm += newVec[j] * newVec[j]
			}
			norm = math.Sqrt(norm)
			for j := range newVec {
				components[i][j] = newVec[j] / norm
			}
		}
	}

	// 5. 차원 축소된 데이터 계산
	reduced := make([][]float64, len(vectors))
	for i := range reduced {
		reduced[i] = make([]float64, targetDim)
		for j := 0; j < targetDim; j++ {
			for k := range vectors[i] {
				reduced[i][j] += (vectors[i][k] - mean[k]) * components[j][k]
			}
		}
	}

	return reduced
}

Locality-Sensitive Hashing

LSH(Locality-Sensitive Hashing)는 고차원 벡터를 해시 함수로 변환하여 유사한 벡터끼리 같은 버킷에 저장하는 기법입니다. 즉, 유사한 벡터는 해시를 통해 근처에 배치되며, 이를 통해 고차원 공간에서 효율적인 근사 검색이 가능합니다.

우리는 얼마나 클러스터링을 할 것인가를 정해야하는데, 이를 Band라는 단위로 구분합니다. Band의 수가 커지면 정확도가 증가할 테고, Band 수가 작아지면 빠르게 대략적인 그룹을 파악할 수 있겠죠.

이렇게 인풋 차원을 쪼개어 각각의 Band로 정의하고, 이 Band 내부에서 클러스터링을 실시합니다. 한번이라도 같은 클러스터에 할당되었다면 이것을 같은 bucket 안에 있다고 말합니다.
이렇게 같은 bucket에 한 번이라도 두 개 이상의 항목이 같은 bucket에 할당되면, 이는 Candidate Similar Combinations로 간주됩니다.

예를 들어, Band3(TF #6~8)에는 C1, C3가 (1, 1, 1)로 모두 포함되어 있고, C4, C5가 (0, 1, 1)로 TF 7, 8에 포함되어 있는 패턴을 보여주어 그룹화할 수 있습니다.

이 때 C2와 같이 단 한 번도 다른 C들과 부분적으로 비슷한 적이 없는 아웃라이어들은 무시합니다. 이렇게 함으로써 모든 문서들을 쌍으로 비슷한 정도를 계산할 필요 없이 유사 문서를 찾아낼 수 있게 됩니다.

min-hasing은 데이터의 차원을 줄여서, 본래 데이터의 클러스터링 결과와 차원 축소된 클러스터링 결과를 비슷하도록 하는 방법입니다. 즉 유사도를 근사적으로 계산하는 방법입니다.

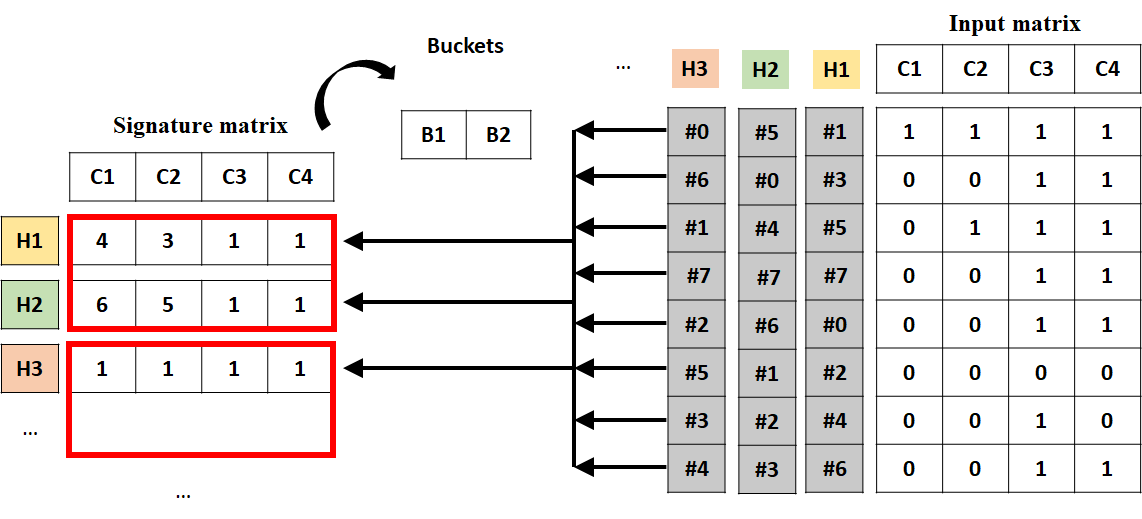
이제 min-hashing으로 만들어진 signature 행렬(H1~3)에 LSH를 적용합니다. 이 때는 B1, B2라는 2가지 버킷으로 클러스터링 되고, 우리는 이제 같은 버킷에 있는 문서들만 유사도를 비교하여 유사한 문서들을 찾을 수 있습니다.

이처럼 PCA로 먼저 데이터 차원을 줄이고 중요한 성분만 남긴 뒤, LSH로 데이터를 해싱하는 방식으로 최적화하면 고차원 벡터를 빠르게 근사 검색하는 ANN을 구현할 수 있습니다.

LSH - Source Code

역시 참고를 위해 아래 코드를 첨부합니다.

type LSHIndex struct {
	hashTables []map[string][]int
	numTables  int
	numBands   int
	bandSize   int
}

// NewLSHIndex는 새로운 LSH 인덱스를 생성합니다
func NewLSHIndex(numTables, numBands, bandSize int) *LSHIndex {
	hashTables := make([]map[string][]int, numTables)
	for i := range hashTables {
		hashTables[i] = make(map[string][]int)
	}
	return &LSHIndex{
		hashTables: hashTables,
		numTables:  numTables,
		numBands:   numBands,
		bandSize:   bandSize,
	}
}

// HashVector는 벡터를 해시값으로 변환합니다
func (lsh *LSHIndex) HashVector(vector []float64, tableIdx int) string {
	rand.Seed(int64(tableIdx))
	hash := ""
    
	for i := 0; i < lsh.numBands; i++ {
		bandHash := 0
		for j := 0; j < lsh.bandSize && (i*lsh.bandSize+j) < len(vector); j++ {
			randVal := rand.Float64()
			if vector[i*lsh.bandSize+j] > randVal {
				bandHash = bandHash*2 + 1
			} else {
				bandHash = bandHash * 2
			}
		}
		hash += fmt.Sprintf("_%d", bandHash)
	}
	return hash
}

// AddToTable은 벡터를 해시 테이블에 추가합니다
func (lsh *LSHIndex) AddToTable(vector []float64, idx int) {
	for i := 0; i < lsh.numTables; i++ {
		hash := lsh.HashVector(vector, i)
		lsh.hashTables[i][hash] = append(lsh.hashTables[i][hash], idx)
	}
}

// GetCandidates는 쿼리 벡터와 유사한 후보들을 반환합니다
func (lsh *LSHIndex) GetCandidates(query []float64) map[int]bool {
	candidateSet := make(map[int]bool)
    
	for i := 0; i < lsh.numTables; i++ {
		hash := lsh.HashVector(query, i)
		if candidates, exists := lsh.hashTables[i][hash]; exists {
			for _, idx := range candidates {
				candidateSet[idx] = true
			}
		}
	}
	return candidateSet
}

Result

이제 PCA, LSH 기반 최적화를 진행한 ANN 벡터유사도 검색을 아래와 같이 새로 작성할 수 있습니다.

func (db *VectorDB) Search(query []float64, topK int) []models.SearchResult {
	// LSH를 사용한 ANN 검색
	candidateSet := db.lshIndex.GetCandidates(query)
	results := make([]models.SearchResult, 0)

	// 후보 검색 (근사 이웃 검색)
	for idx := range candidateSet {
			similarity := utils.CosineSimilarity(query, db.Products[idx].Vector)
			results = append(results, models.SearchResult{
					Product:    db.Products[idx],
					Similarity: similarity,
			})
	}

	// 결과가 없으면 전체 검색 (폴백 메커니즘)
	if len(results) == 0 {
			for _, product := range db.Products {
					similarity := utils.CosineSimilarity(query, product.Vector)
					results = append(results, models.SearchResult{
							Product:    product,
							Similarity: similarity,
					})
			}
	}

	// 정렬 및 상위 K개 반환
	sort.Slice(results, func(i, j int) bool {
			return results[i].Similarity > results[j].Similarity
	})

	if len(results) > topK {
			results = results[:topK]
	}

	return results
}

main 파일에서 앞서 넣어주었던 데이터셋들을 기반으로 아래와 같이 검색을 시행해보겠습니다.

func main() {
    // 벡터 데이터베이스 생성
    db := database.NewVectorDB()

    // 상품 데이터 추가
    db.AddProduct(models.Product{
        ID:          1,
        Name:        "캐주얼 티셔츠",
        Price:       29900,
        Vector:      []float64{0.3, 0.9, 0.1, 0.4, 0.7},
        Category:    "의류",
        Description: "편안한 데일리 티셔츠",
    })

    // ... datasets
    
    
    // 검색 시나리오 예시들

    // 1. 캐주얼한 여름옷 찾기
    fmt.Println("1. 캐주얼한 여름옷 검색:")
    summerCasualQuery := []float64{0.3, 0.9, 0.1, 0.2, 0.9} // 저가, 매우 캐주얼, 여름
    results := db.Search(summerCasualQuery, 2)
    printSearchResults(results)

    // 2. 고급 정장 스타일 찾기
    fmt.Println("\n2. 고급 정장 스타일 검색:")
    formalQuery := []float64{0.8, 0.1, 0.9, 0.1, 0.5} // 고가, 매우 포멀
    results = db.Search(formalQuery, 2)
    printSearchResults(results)

    // 3. 적당한 가격의 스포츠웨어 찾기
    fmt.Println("\n3. 가성비 스포츠웨어 검색:")
    sportsQuery := []float64{0.4, 0.2, 0.1, 0.9, 0.7} // 중저가, 매우 스포티
    results = db.Search(sportsQuery, 2)
    printSearchResults(results)
  
  
  // 검색 결과 출력을 위한 헬퍼 함수
func printSearchResults(results []models.SearchResult) {
    for _, result := range results {
        fmt.Printf("상품명: %s\n", result.Product.Name)
        fmt.Printf("가격: %.0f원\n", result.Product.Price)
        fmt.Printf("카테고리: %s\n", result.Product.Category)
        fmt.Printf("설명: %s\n", result.Product.Description)
        fmt.Printf("유사도: %.2f\n\n", result.Similarity)
    }
}

결과는 아래와 같이 유사도가 높은 것들을 top 2개(특정 유사도 이상) 선택한 결과물입니다.

1. '캐주얼한 여름옷' 검색:
상품명: 캐주얼 티셔츠
가격: 29900원
카테고리: 의류
설명: 편안한 데일리 티셔츠
유사도: 0.98

상품명: 캐주얼 셔츠
가격: 49900원
카테고리: 의류
설명: 데일리 캐주얼 셔츠
유사도: 0.95


2. '고급 정장 스타일' 검색:
상품명: 정장 셔츠
가격: 89000원
카테고리: 의류
설명: 고급 비즈니스 셔츠
유사도: 1.00


3. '가성비 스포츠웨어' 검색:
상품명: 운동용 반팔
가격: 39900원
카테고리: 의류
설명: 기능성 스포츠 웨어
유사도: 1.00

상품명: 캐주얼 티셔츠
가격: 29900원
카테고리: 의류
설명: 편안한 데일리 티셔츠
유사도: 0.76

보시다시피 vector기반으로 잘 선택되는 것을 알 수 있으며, 상품을 등록할 때 정량적인 기준을 바탕으로 적절한 vector를 설정하는 것이 매우 중요함을 직관적으로 알 수 있습니다.

PCA result

    // PCA 예시
    vectors := make([][]float64, len(db.GetProducts()))
    for i, product := range db.GetProducts() {
        vectors[i] = product.Vector
    }
    
    reducedVectors := dimension.PCA(vectors, 3)
    
    fmt.Println("차원 축소된 벡터들:")
    for i, vec := range reducedVectors {
        fmt.Printf("상품 %s의 축소된 벡터: %v\n", db.GetProducts()[i].Name, vec)
    }