시간복잡도...!
암기할 필요가 있을까? 싶지만 알면 좋다고 생각한다. (경험상 면접에서 물어보기도 하고..ㅋㅋ)
알고리즘의 분석 결과는 입력되는 데이터의 수 N에 대하여 수행 시간을 함수 관계로 표현한다.
그리고 아래는 그 종류이다.
O(1)
입력되는 자료의 수와 관계없이 일정한 시간을 갖는 알고리즘을 말한다.
O(logN)
일단 log의 성질상 밑수의 값에 따라서 결과가 달라지지만 일단 밑수는 10으로 가정하자.
만약 입력되는 자료의 수에 따라 실행시간이 logN의 관계를 만족한다면 N이 증가함에 따라 실행시간이 조금씩 늘어난다.
(기본적인 수학인데, N이 1000개랑 10,000개랑 다르다는게 직관적으로 알 수 있다.)
이 유형은 주로 커다란 문제를 일정한 크기를 갖는 작은 문제로 쪼갤때 나타나는 유형이다.
logN의 시간복잡도를 보이는 알고리즘은 아주 좋은 성능을 보여준다고 생각하면 된다!
O(N)
입력된 자료의 수에 따라 Linear하게 실행시간이 걸리는 경우다.
O(NlogN)
이 유형은 커다란 문제를 독립적인 작은 문제로 쪼개서 문제를 해결하고, 나중에 다시 그것들을 하나로 모으는 경우에 나타난다.
그도 그럴것이 위의 logN이 "커다란 문제를 일정한 크기를 갖는 작은 문제로 쪼개는 유형"에 많이 나오다고 했는데, 거기서 N이 곱해지기걸 보면 이해하기 수월하다.
N이 두배 늘언면 실행 시간은 두배보다 약간 더 늘어나는데, 성능이 좋은 정렬 알고리즘의 실행시간은 NlogN에 비례한다.
O(N^2)
이 유형은 이중 loop내에서 입력된 자료를 처리하는 경우에 나타난다.
N이 커질수록 실행 시간은 감당하기 어려울만큼 커지게 되는데, 이런 유형의 알고리즘은 데이터의 숫자가 많은 경우에는 부적절하다.
N이 2배 늘어나면, 실행시간은 4배가 늘어난다...ㅎㄷㄷ
O(N^3)
이 유형은 탁보면 척! 하겠지만 삼중 loop 내에서 자료를 처리하는 경우에 나타난다.
따라서 처리해야할 자료의 양이 많다면, 이런 알고리즘은 부적절한데 N이 2배가 된다면 실행시간은 8배로 늘어난다...
O(2^N)
입력되는 데이터의 수가 늘어남에 따라 급격하게 실행시간이 늘어난다.
이 유형은 흔하지는 않지만, 초기에 알고리즘을 작성하는 단계에서 발견될 수 있지만 개발과정에서 대부분 보다 좋은 성능의 알고리즘으로 개선된다.
N이 2배가 늘어나면 실행시간은 제곱으로 늘어나게 된다.
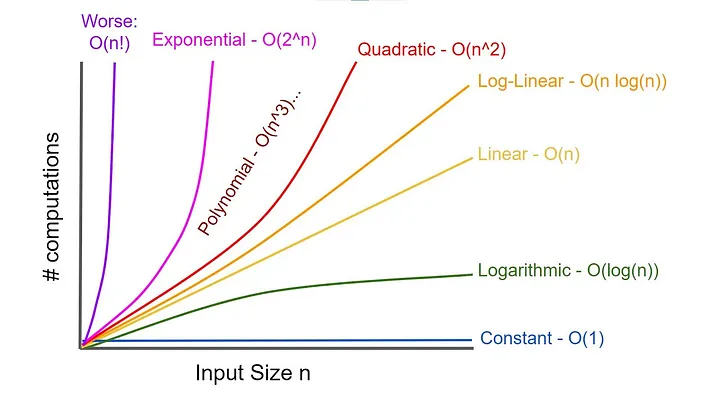
image source
아무리 그래도 N팩토리얼은 좀...ㅋㅋ
