백준 4256(트리)

jh Seo·2023년 1월 31일

백준 트리 한번에 못 푼 문제

백준

목록 보기

124/194

개요

백준 4256번: 트리

입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스의 첫째 줄에는 노드의 개수 n이 주어진다. (1 ≤ n ≤ 1,000) BT의 모든 노드에는 1부터 n까지 서로 다른 번호가 매겨져 있다. 다음 줄에는 BT를 전위 순회한 결과, 그 다음 줄에는 중위 순회한 결과가 주어진다. 항상 두 순회 결과로 유일한 이진 트리가 만들어지는 경우만 입력으로 주어진다.
출력
각 테스트 케이스마다 후위 순회한 결과를 출력 한다.

접근 방식

기본적으로 중위순회 값이 나올때까지 전위 순회값들을 연결해주고
중위순회 값과 일치하는 값이 나오면 처리를하고 이런식으로 짜려했으나 감이 안잡혔다.
검색해본 결과, 전위 순회와 중위 순회의 성질을 이용하는 문제였다.
전위 순회는 첫 값을 루트값을 가진다.
후위 순회 수열에서 해당 루트값을 찾고, 루트 인덱스의 다음 인덱스들은
루트의 오른쪽 서브트리 원소들이고, 루트 인덱스의 이전 인덱스들은
왼쪽의 서브트리 원소들이다.
이런 성질들로 생각해낸 건, 각 서브트리의 루트값을 매개변수로 받는
재귀함수 MakeTree다.

void MakeTree(int rootNode,vector<int>::iterator inOrderBegin,vector<int>::iterator inOrderEnd)

매개 변수로 루트노드 값과, 중위 순회의 원소 중
해당 루트의 서브트리에 포함되는 원소들의 범위를 매개변수로 받는다.
만약 서브트리의 원소 갯수가 1개이하면
바로 return해준다.

	//루트 노드가 0이면 return
	if (inOrderBegin >= inOrderEnd-1) return;

그 후, 전위 순회 벡터와 중위 순회 벡터에서의 루트노드 위치를 찾고
preOrderIter, inOrderIter에 넣어준다.

	vector<int>::iterator preOrderIter, inOrderIter;
	for (auto iter = inOrderBegin; iter != inOrderEnd; ++iter) {
		if (*iter == rootNode) {
				inOrderIter = iter;
				break;
		}
		if (iter == inOrderEnd - 1) {
			inOrderIter = inOrderEnd - 1;
		}
	}

	for (auto iter1 = preOrder.begin(); iter1 != preOrder.end(); ++iter1) {
		if (*iter1 == rootNode) {
				preOrderIter = iter1;
				break;
		}
		if (iter1 == preOrder.end() - 1) {
			preOrderIter = preOrder.end() - 1;
		}
	}

해당 서브트리의 루트 노드 rootNode의 오른쪽 자식값은
오른쪽 서브트리의 원소 중 전위 순회벡터에서 제일 인덱스가 작은 값이다.
전위 순회 특성상 어떤 서브트리에서라도 루트노드를 제일 먼저 방문하기 때문이다.

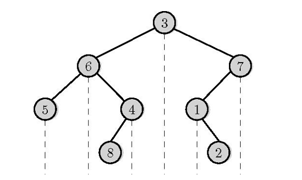
문제의 예로 생각해보면 루트노드가 3일때 해당 서브트리의
중위 순회 벡터 원소들은 5 6 8 4 3 1 2 7 이고,
이 원소 중 루트 노드 다음 인덱스의 원소들은 1,2,7이다.
-> 3의 오른쪽 서브트리와 일치한다.
1,2,7의 전위 순회 벡터에서의 인덱스는 7,1,2 순서다.
-> 제일 인덱스가 작은 7이 오른쪽 서브트리의 루트값과 일치한다.
```
//중위 순회 벡터에서의 rootNode의 위치인 inOrderIter값 다음 인덱스부터 탐색
	for (auto iter=inOrderIter+1; iter != inOrderEnd; ++iter) {
		//min노드에 오른쪽서브트리의 루트노드 찾아줌-> 오른쪽서브트리의 노드값들중에 전위순회에서 제일먼저 나온 노드가 루트노드
		if (rightSubTreeRootNodeIdx > preOrderIndex[*iter]) {
			rightSubTreeRootNodeIdx = preOrderIndex[*iter];
			rightSubTreeRootNode = *iter;
		}
	}
```

루트노드의 왼쪽 자식은
전위 순회 벡터에서 루트값 다음 인덱스의 원소다.

   	//왼쪽 자식노드가 있다면
		if(preOrderIter!=preOrder.end()-1)
		//왼쪽 서브트리의 루트노드는 전위순회벡터에서 바로 다음 값임
		leftSubTreeRootNode = *(preOrderIter + 1);

루트노드의 왼쪽 , 오른쪽 서브트리의 루트값을 찾았으니 미리 선언해둔 왼쪽, 오른쪽 자식 값 배열과 부모 값 배열에 저장해준다.

//왼쪽 자식 노드 있을때만
	if (preOrderIter != preOrder.end() - 1)
	leftChildren[rootNode] = leftSubTreeRootNode;
	//오른쪽 자식 노드 있을 때만
	if(inOrderIter!=inOrderEnd-1)
	rightChildren[rootNode] = rightSubTreeRootNode;
	//왼쪽 자식노드 있을때만
	if (preOrderIter != preOrder.end() - 1)
	parent[leftSubTreeRootNode] = rootNode;
	//오른쪽 자식노드 잇을때만
	if (inOrderIter != inOrderEnd - 1)
	parent[rightSubTreeRootNode] = rootNode;

하지만 위의 방식만으로 오른쪽 왼쪽을 구분하면 문제점이 있는데,
루트노드의 왼쪽 자식이없고 오른쪽 자식만 있을 때,
전위 순회에서 다음값이 오른쪽 자식을 가리키게되어
오른쪽 자식값과 왼쪽 자식값이 같은 값을 가리킨다.
따라서 예외처리를 해줘야한다.
```
	//왼쪽자식이없고 오른쪽자식만 있을 경우 전위순회에서 다음값과 중위순회 다음값이 일치함
	if (leftSubTreeRootNode == rightSubTreeRootNode) {
		leftSubTreeRootNode = 0;
	}
```

그 후 재귀함수를 이용해 반복해주면 된다.

		//왼쪽 자식노드 있다면 해당 노드를 루트로 왼쪽 서브트리 완성
		if (preOrderIter != preOrder.end() - 1)
		MakeTree(leftSubTreeRootNode,inOrderBegin,inOrderIter);
		//오른쪽 자식노드 있다면 해당 노드를 루트로 오른쪽 서브트리 완성한다.
		if (inOrderIter != inOrderEnd - 1)
		MakeTree(rightSubTreeRootNode,inOrderIter+1,inOrderEnd);

전체 코드

#include<iostream>
#include<vector>
#include<algorithm>
#include<map>

using namespace std;
vector<int> inOrder;
vector<int> preOrder;
//전위순회 원소들의 인덱스 저장용
map<int, int> preOrderIndex;

//값들은 1부터들어오므로 0으로 초기화해도 됨
int parent[1001];
int leftChildren[1001];
int rightChildren[1001];

void init() {
	inOrder.clear();
	preOrder.clear();
	preOrderIndex.clear();
	fill(parent, parent + 1001, 0);
	fill(leftChildren, leftChildren + 1001, 0);
	fill(rightChildren, rightChildren+ 1001, 0);
}
void Solution();

void Input() {
	int N=0,Nodes=0,tmptreeNodes=0;
	cin >> N;
	for (int i = 0; i < N; i++) {
		cin >> Nodes;
		init();
		for (int j = 0; j < Nodes; j++) {
			cin >> tmptreeNodes;
			preOrder.push_back(tmptreeNodes);
			preOrderIndex[tmptreeNodes] = j;
		}
		for (int j = 0; j < Nodes; j++) {
			cin >> tmptreeNodes;
			inOrder.push_back(tmptreeNodes);
		}
		Solution();
		cout << '\n';
	}
}

//rootNode기준으로 왼쪽 서브트리의 루트, 오른쪽 서브트리의 루트를 구해서 rootNode와 관계정립시켜주고 각 서브트리의 루트노드로 다시 재귀
//서브트리의 루트와 inorder벡터에서의 해당 서브트리의 위치를 iterator로 넣어줌  
void MakeTree(int rootNode,vector<int>::iterator inOrderBegin,vector<int>::iterator inOrderEnd) {
	//루트 노드가 0이면 return
	if (inOrderBegin >= inOrderEnd-1) return;

	//오른쪽 서브트리 노드 루트값, 왼쪽 서브트리 노드 루트값, 오른쪽 서브트리중에 인덱스 제일 작은 값 저장용 변수
	int rightSubTreeRootNode = 1002, leftSubTreeRootNode = 1002, rightSubTreeRootNodeIdx = 1002;
	vector<int>::iterator preOrderIter, inOrderIter;
	for (auto iter = inOrderBegin; iter != inOrderEnd; ++iter) {
		if (*iter == rootNode) {
				inOrderIter = iter;
				break;
		}
		if (iter == inOrderEnd - 1) {
			inOrderIter = inOrderEnd - 1;
		}
	}

	for (auto iter1 = preOrder.begin(); iter1 != preOrder.end(); ++iter1) {
		if (*iter1 == rootNode) {
				preOrderIter = iter1;
				break;
		}
		if (iter1 == preOrder.end() - 1) {
			preOrderIter = preOrder.end() - 1;
		}
	}
	//무조건 자식 두개 다있따고 가정하고 품;

	//오른쪽 서브트리
	for (auto iter=inOrderIter+1; iter != inOrderEnd; ++iter) {
		//min노드에 오른쪽서브트리의 루트노드 찾아줌-> 오른쪽서브트리의 노드값들중에 전위순회에서 제일먼저 나온 노드가 루트노드
		if (rightSubTreeRootNodeIdx > preOrderIndex[*iter]) {
			rightSubTreeRootNodeIdx = preOrderIndex[*iter];
			rightSubTreeRootNode = *iter;
		}
	}
	//왼쪽 자식노드가 있다면
	if(preOrderIter!=preOrder.end()-1)
	//왼쪽 서브트리의 루트노드는 전위순회벡터에서 바로 다음 값임
	leftSubTreeRootNode = *(preOrderIter + 1);

	//왼쪽자식이없고 오른쪽자식만 있을 경우 전위순회에서 다음값과 중위순회 다음값이 일치함
	if (leftSubTreeRootNode == rightSubTreeRootNode) {
		leftSubTreeRootNode = 0;
	}
	//왼쪽 자식 노드 있을때만
	if (preOrderIter != preOrder.end() - 1)
	leftChildren[rootNode] = leftSubTreeRootNode;
	//오른쪽 자식 노드 있을 때만
	if(inOrderIter!=inOrderEnd-1)
	rightChildren[rootNode] = rightSubTreeRootNode;
	//왼쪽 자식노드 있을때만
	if (preOrderIter != preOrder.end() - 1)
	parent[leftSubTreeRootNode] = rootNode;
	//오른쪽 자식노드 잇을때만
	if (inOrderIter != inOrderEnd - 1)
	parent[rightSubTreeRootNode] = rootNode;

	//왼쪽 자식노드 있다면 해당 노드를 루트로 왼쪽 서브트리 완성
	if (preOrderIter != preOrder.end() - 1)
	MakeTree(leftSubTreeRootNode,inOrderBegin,inOrderIter);
	//오른쪽 자식노드 있다면 해당 노드를 루트로 오른쪽 서브트리 완성한다.
	if (inOrderIter != inOrderEnd - 1)
	MakeTree(rightSubTreeRootNode,inOrderIter+1,inOrderEnd);
}

//후위 순회 방식으로 답 출력
void PrintInOrder(int Node) {
	if (Node == 0) return;
	PrintInOrder(leftChildren[Node]);
	PrintInOrder(rightChildren[Node]);
	cout << Node<<" ";
}

void Solution() {
	int rootNode = preOrder[0];
	MakeTree(rootNode,inOrder.begin(),inOrder.end());
	PrintInOrder(rootNode);
}
int main() {
	ios_base::sync_with_stdio(0);
	cin.tie(0);
	Input();

}

문풀후생

처음엔 무조건 왼쪽 오른쪽 자식값이 다 있다고 가정하고 풀었다가 틀리고,
예외 처리한 후엔 오른쪽 자식만 있을 때,
전위 순회값도 오른쪽 자식값을 가리키는걸 생각을 못해서 또 틀렸다..
여러모로 시간을 많이 할애한 문제다

jh Seo

코딩 창고!

이전 포스트

백준2250(트리의 높이와 너비)

다음 포스트

백준 4256(트리)

백준

개요

접근 방식

전체 코드

문풀후생

백준2250(트리의 높이와 너비)

백준1967(트리의 지름)

0개의 댓글