백준1967(트리의 지름)

jh Seo·2023년 2월 2일

백준 트리 한번에 푼 문제

백준

목록 보기

125/194

개요

백준1967번: 트리의 지름

입력
파일의 첫 번째 줄은 노드의 개수 n(1 ≤ n ≤ 10,000)이다. 둘째 줄부터 n-1개의 줄에 각 간선에 대한 정보가 들어온다. 간선에 대한 정보는 세 개의 정수로 이루어져 있다. 첫 번째 정수는 간선이 연결하는 두 노드 중 부모 노드의 번호를 나타내고, 두 번째 정수는 자식 노드를, 세 번째 정수는 간선의 가중치를 나타낸다. 간선에 대한 정보는 부모 노드의 번호가 작은 것이 먼저 입력되고, 부모 노드의 번호가 같으면 자식 노드의 번호가 작은 것이 먼저 입력된다. 루트 노드의 번호는 항상 1이라고 가정하며, 간선의 가중치는 100보다 크지 않은 양의 정수이다.
출력
첫째 줄에 트리의 지름을 출력한다.

접근방식

첫 번째 방식

이진트리라는 말이 없으므로 2차원 벡터를 만들어
벡터의 부모값 인덱스에 자식값을 계속 push_back()하는 형태로
트리를 구현하였다.
부모와 자식값을 문제에서 명확히 알려준다.
-> 방문여부를 신경 안 써도 된다.
무방향그래프 형식의 그냥 노드끼리 연결이라면 방문여부 배열을 따로 만들어서
현재 노드와 연결된 노드가 이미 방문한 부모노드인지 체크하고 continue를 해야함.

부모와 자식값을 구조체로 구현 후, STL의 map을 이용해
가중치를 매핑했다.

struct parentAndChild {
	int parent;
	int child;
	//해시충돌에서 키비교용으로 필요함
	bool operator<(const parentAndChild& other) const{
		if (parent == other.parent) return child < other.child;
		return parent<other.parent;
	}
};
//parent, child값의 가중치저장용 해시맵
map<parentAndChild, int> distInfo;

이 문제는 루트노드 1을 중심으로 한 트리의 지름을 구하는 문제가 아니다.

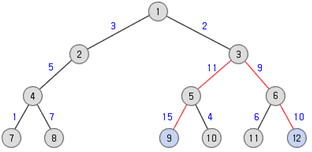
예제에서 친절하게 줬듯이 3번 노드가 중심인 트리에서
9 - 5 -3 - 6 - 12의 연결이 지름이 45로 제일 길다.
그러므로 각 서브트리에서도 지름을 구해야한다.
따라서 각 서브트리의 루트노드를 매개변수로 하는 재귀함수
int SearchTree(int node)를 구현하였다.
이 함수는 서브트리의 루트노드부터 리프노드까지의 최대 거리를 반환한다.
DFS방식으로 탐색하며,
함수 내부에서 루트노드에서 리프노드까지의 거리를 전부 비교 후
최대 거리와 두번째로 긴 거리를 구한다.

두 번째 방식

이 문제의 새로운 방식을 봤는데 [라이의 블로그] 이 분의 블로그에서 봤다.
루트노드에서 제일 먼 노드 중 하나를 탐색한다
(예시로 제일 먼 노드를 F 노드라고 하자).
F 노드는 무조건 트리의 지름의 끝점이다.
F 노드에서 제일 먼 노드까지의 거리가 트리의 지름이다.

이유는

F노드와 G노드가 각 트리의 지름의 끝점이라고 하자.
F노드가 제일 먼 노드중 하나라고 했으므로
루트에서 F노드까지의 거리>= 루트에서 G노드까지의 거리이다.
트리의 지름에 해당하는 노드 중 제일 깊이가 낮은 노드를 R이라고 하자.
트리의 지름은
(루트->F노드 거리)- (루트->R노드 거리) + (루트->G노드 거리)-(루트->R노드 거리) 이렇게 이다. (F노드-R노드-G노드 이렇게 연결됨)
만약 F노드가 트리의 끝점이 아니라 다른 H노드가 트리의 끝 점이라고 해보자.
그럼 F-R-G이렇게 연결이아니라 H-R-G이렇게 연결되어야 하는 데,
이렇게 되면 (루트->R노드->F노드의 거리) < ( 루트->R노드->H노드의거리) 가 되어
F노드가 루트에서 제일 먼 노드 중 하나라는 전제조건이 망가져 모순이다.

따라서 루트에서 제일 먼 노드 잡고
해당 노드에서 제일 먼 노드를 구해 두 노드 사이 거리를 구하면 답이된다.

첫번째 방식 코드

(각 서브트리마다 트리의 지름값 조사)

#include<iostream>
#include<vector>
#include<algorithm>
#include<map>

using namespace std;
//부모 자식연결
vector<vector<int>> tree;

struct parentAndChild {
	int parent;
	int child;
	//map에서 키비교용으로 필요함
	bool operator<(const parentAndChild& other) const{
		if (parent == other.parent) return child < other.child;
		return parent<other.parent;
	}
};
//parent, child값의 가중치저장용 맵
map<parentAndChild, int> distInfo;

//답으로 출력할 지름
int maxRadius=0;

void Input() {
	//N, 부모값, 자식값, 가중치
	int N = 0,parent=0,child=0,dist=0;
	cin >> N;
	//노드는 1부터 들어옴
	tree.resize(N+1);
	for (int i = 0; i < N-1; i++) {
		cin >> parent >> child >> dist;
		//부모값에 자식값 푸시해줌
		tree[parent].push_back(child);
		distInfo[{parent, child}] = dist;
	}
}

//루트인 node 노드에서 제일 멀리떨어진 노드와의 거리 반환(각 자식들에서 재귀함수를 통해 제일 먼 거리와 두 번째로 먼 거리 찾아놓음.)
int SearchTree(int node) {
	//node 노드의 자식노드가 없다면 0리턴
	if (tree[node].size() == 0) return 0;

	//자식 중에 제일 긴 길이
	int longest=0,
		//자식중 두번째로 긴 길이
		secondLongest=0,
		// node의 자식 중 하나로 파고들어갔을때의 나온 리프노드부터 node노드까지의 거리
		lengthOfEachChildRoute=0,
		//node노드의 각 자식에서 node노드까지의 길이
		tmpLengthNodeToElem=0;

	//node 노드의 각 자식마다 재귀를 통해 
	for (int elem : tree[node]) {
		//노드에서 각자식까지의 길이 초기화후, 값 넣어줌
		tmpLengthNodeToElem= 0;
		tmpLengthNodeToElem = distInfo[{node, elem}];
		//elem자식으로 내려갔을 때의 총 길이
		lengthOfEachChildRoute = tmpLengthNodeToElem;
		lengthOfEachChildRoute += SearchTree(elem);
		//제일 길다면 longest에 저장 
		//갱신될때 지금 longest를 second로 넘겨줘야함!!!!
		if (longest < lengthOfEachChildRoute) {
			secondLongest = longest;
			longest = lengthOfEachChildRoute;
		}
		//두번째로 길다면 secondLongest에 저장 lengthOfChildRoute< longest로 했더니 같을때 체크를 못함
		else if (lengthOfEachChildRoute<=longest && lengthOfEachChildRoute>secondLongest)
			secondLongest = lengthOfEachChildRoute;
	}
	//모든 자식노드에 대해 DFS가 끝나면 최대거리와 두번째로 긴 거리가 저장됨 
	//최대 지름값 갱신
	maxRadius = max(maxRadius, longest + secondLongest);
	//node에서 출발해서 자식값중 제일 먼 거리를 리턴 
	return longest;
}


void Solution() {
	//루트노드는 1로 정해줌
	SearchTree(1);
	cout << maxRadius;
}

int main() {
	Input();
	Solution();
}

두번째 방식 코드

(루트에서 제일 먼 노드값 찾고 해당 노드에서 제일 먼 노드 찾아서 거리 계산 )

#include<iostream>
#include<vector>
#include<algorithm>
#include<map>

using namespace std;
//부모 자식연결
vector<vector<int>> tree;
//방문여부 처리 벡터
vector<bool> visited;

struct parentAndChild {
	int parent;
	int child;
	//맵에서 키비교용으로 필요함
	bool operator<(const parentAndChild& other) const{
		if (parent == other.parent) return child < other.child;
		return parent<other.parent;
	}
};
//parent, child값의 가중치저장용 맵
map<parentAndChild, int> distInfo;

//답 출력용
int farthestLength=0,farthestElem=0;

void Input() {
	//N, 부모값, 자식값, 가중치
	int N = 0,parent=0,child=0,dist=0;
	cin >> N;
	//노드는 1부터 들어옴
	tree.resize(N+1);
	visited.resize(N + 1);
	fill(visited.begin(), visited.end(), false);

	for (int i = 0; i < N-1; i++) {
		cin >> parent >> child >> dist;
		//부모값에 자식값 푸시해줌
		tree[parent].push_back(child);
		tree[child].push_back(parent);
		distInfo[{parent, child}] = dist;
		distInfo[{child, parent}] = dist;
	}
}
// 재귀를 통해 Node에서 제일 먼 거리의 노드를 찾아 해당 노드와 거리를 
// farthestLength=0,farthestElem에 저장하는 함수
// 각 재귀에서 루트노드에서 Node노드까지의 총 거리를 totlength로 넘겨준다.
void SearchFarthest(int Node,int totlength) {
	//양방향 그래프로 parent랑 child랑 서로 연결되어있으므로 
	//Node값 방문처리하여 부모값 다시 방문 못하게 하기
	visited[Node] = true;
	//리프노드라면 return
	if (tree[Node].size() == 0) return;
	//Node노드의 인접 노드들 중에서
	for (int elem : tree[Node]) {
		//방문한값이면 부모 노드이므로 continue
		if (visited[elem]) continue;
		//Node와 elem사이의 가중치값 가져옴
		int lengthNodeToElem = distInfo[{Node,elem}];
		//totlength에 Node에서 elem사이의 가중치값 더해주고 
		totlength += lengthNodeToElem;
		//제일 먼 거리값이 현재 거리보다 작은값이면 갱신
		if (farthestLength < totlength) {
			//제일 먼 노드값도 저장해줌
			farthestElem = elem;
			farthestLength = totlength;
		}
		SearchFarthest(elem,totlength);
		//각 자식에서 dfs끝나면 totlength값 다시 초기화시켜줌
		totlength -= lengthNodeToElem;
	}

}


void Solution() {
	//루트노드는 1로 정해줌
	SearchFarthest(1,0);
	fill(visited.begin(), visited.end(), false);
	SearchFarthest(farthestElem,0);
	cout << farthestLength;
}

int main() {
	Input();
	Solution();
}

문풀후생

두 가지 실수를 해서 시간을 엄청 썼는데,

첫 번째는 unordered_map이 그냥 키 값을 정렬하지 않은 채로 밸류값을
매핑해주므로 굳이 정렬이 필요없어서 map대신 unordered_map을 사용했다.
하지만 unordered_map에 구조체를 키로 사용하려했으나 계속 오류가 나서
고민하다가 검색을 하였다.
구조체를 키로 사용하려면 특수 해시함수를 따로 만들어야하고
구글링을 한 결과 임시로 xor방식으로 만든 해시함수는
동일값은 0으로 매핑해서 충돌이 많이 난다고 한다.

[링크]구조체를 unordered_map의 키로 사용하는 법

따라서 구조체 비교함수를 작성하여 map을 이용해 구현하였다.
두 번째는 line 63
```
	if (longest < lengthOfEachChildRoute) {
		secondLongest = longest;
		longest = lengthOfEachChildRoute;
	}
```
이 부분에서 제일 긴 값을 second값으로 넘겨줘야하는 부분이 중요한데
```
	if (longest < lengthOfEachChildRoute) {
		longest = lengthOfEachChildRoute;
	}
```
이런식으로 그냥 제일 긴 값을 갱신만 하다보니 원하는 대로 작동을 하지 않았다.
이렇게 되면 재귀 끝날때마다 제일 긴 값이 계속 갱신되는 테스트케이스가
들어오면 두번째로 긴 변수에는 계속 0이 들어가있고 갱신이 되지 않는다.