지난 글에서는 사과, 파인애플, 바나나에 있는 각 픽셀의 평균값을 구해서 가장 가까운 사진을 골랐다. 이 경우에는 사과, 파인애플, 바나나 사진임을 미리 알고 있었기 때문에 각 과일의 평균을 구할 수 있었다. 하지만 진짜 비지도 학습에서는 사진에 어떤 과일이 들어 있는지 알지 못한다.
이런 경우에 바로 k-평균 군집 알고리즘이 평균값을 자동으로 찾아준다.
이 평균값이 클러스터의 중심에 위치하기 때문에 클러스터 중심 또는 센터로이드(centeroid)라 부른다.
k-평균 알고리즘
k-평균 알고리즘은 다음과 같다.
- 무작위로 k개의 클러스터 중심을 정한다.
- 각 샘플에서 가장 가까운 클러스터 중심을 찾아 해당 클러스터의 샘플로 지정한다.
- 클러스터에 속한 샘플의 평균값으로 클러스터 중심을 변경한다.
- 클러스터 중심에 변화가 없을 때 까지 2번으로 돌아가 반복한다.
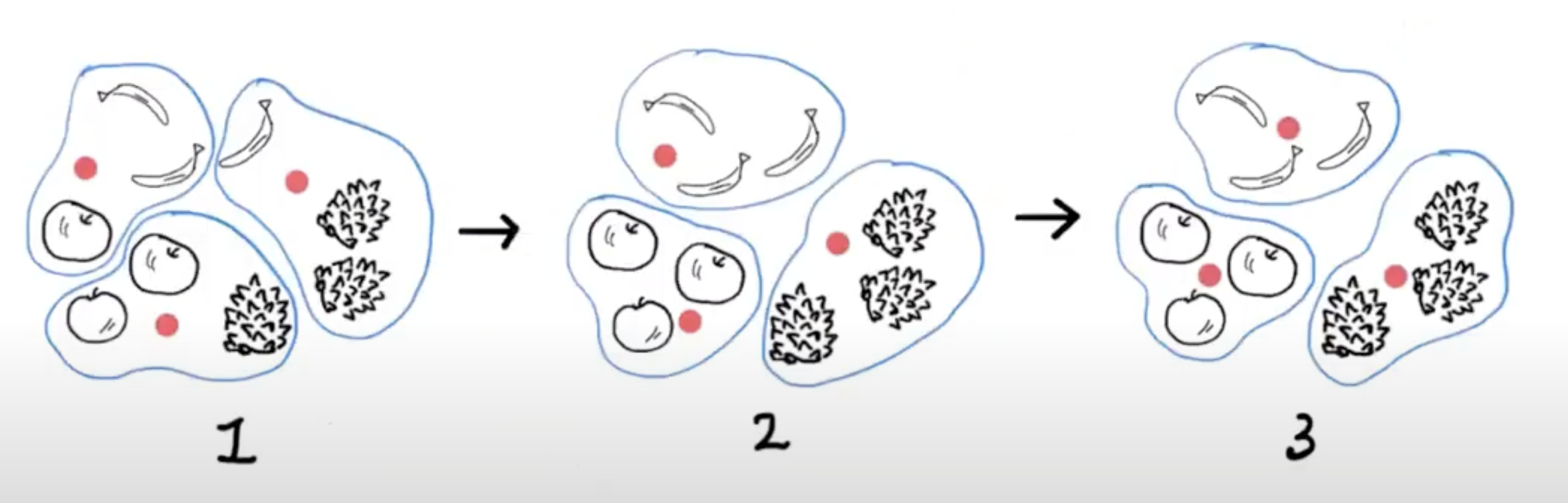
먼저 3개의 클러스터 중심(빨간 점)을 랜덤하게 지정한다(1번 그림). 그리고 클러스터 중심에서 가장 가까운 샘플을 하나의 클러스터로 묶는다.
그 다음 클러스터의 중심을 다시 계산하여 다음 가장 가까운 샘플을 다시 클러스터로 묶는다(2번 그림). 이제 3개의 클러스터에 바나나, 파인애플, 사과가 3개씩 올바르게 묶여있다. 다시 한번 클러스터 중심을 계산하여 빨간 점을 클러스터의 가운데 부분으로 이동시킨다.
이동된 클러스터 중심에서 다시 한번 가장 가까운 샘플을 클러스터로 묶는다(3번 그림). 중심에서 가장 가까운 샘플은 이전 클러스터(2번 그림)과 동일하다. 따라서 클러스터에 변동이 없으므로 k-평균 알고리즘을 종료한다.
k-평균 알고리즘은 처음에는 랜덤하게 클러스터 중심을 선택하고 점차 가장 가까운 샘플을 중심으로 이동하는 간단한 알고리즘이다.
데이터 준비하기
!wget https://bit.ly/fruits_300_data -O fruits_300.npy
import numpy as np
import matplotlib.pyplot as pltfruits = np.load('fruits_300.npy')
fruits_2d = fruits.reshape(-1, 100*100)from sklearn.cluster import KMeans
#클러스터는 3개
km = KMeans(n_clusters=3, random_state=42)
km.fit(fruits_2d)비지도학습이므로 fit() 메서드에 타깃 데이터를 사용하지 않는다.
군집된 결과는 KMeans 클래스 객체에 labels_ 속성에 저장된다. labels 배열의 길이는 샘플 개수와 같다. n_cluster=3으로 3개의 군집을 설정하였으니 label 배열의 값은 0, 1, 2중 하나이다.
print(km.labels_)
#출력값: [2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 0 2 0 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 0 0 2 2 2 2 2 2 2 2 0 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1]레이블값 0, 1, 2와 레이블 순서는 어떤 의미도 없다. 실제 레이블 0, 1, 2가 어떤 과일을 주로 모았는지 알아보려면 직접 이미지를 출력하는 것이 최선이다.
그 전에 0, 1, 2로 모은 샘플 개수를 확인해보자.
#km.labels_의 고유한 값과 그 값이 나온 갯수 출력
print(np.unique(km.labels_, return_counts=True))
#출력값: (array([0, 1, 2], dtype=int32), array([111, 98, 91]))첫 번째 클러스터(0)은 111개의 샘플, 두 번째 클러스터(1)은 98개의 샘플, 세 번째 클러스터(2)는 91개의 샘플을 모았다. 그럼 각 클러스터가 어떤 이미지를 모았는지 그림으로 출력해보자.
draw_fruits() 메서드는 레이블에 따라 모든 이미지를 그려주는 함수.
import matplotlib.pyplot as plt
def draw_fruits(arr, ratio=1):
n = len(arr) #n은 샘플의 개수
rows = int(np.ceil(n/10))
#행의 개수가 1개면 열의 개수는 샘플의 개수, 행이 2개 이상이면 열은 10개로 고정
cols = n if rows < 2 else 10
#subplot 설정
fig, axes = plt.subplots(rows, cols, figsize=(cols*ratio, rows*ratio), squeeze=False)
for i in range(rows): #행마다
for j in range(cols): #열마다
if i * 10 + j < n:
axes[i, j].imshow(arr[i*10 + j], cmap='gray_r')
axes[i, j].axis('off')
plt.show()#레이블이 0일때 이미지 출력
draw_fruits(fruits[km.labels_ == 0])
레이블이 0일때 샘플의 개수 총 111개를 이미지로 출력한 것이다. 이 클러스터는 파인애플을 의미하는 것같지만, 사과와 바나나가 조금씩 섞여 있는 것 같다.
#레이블이 1일때 출력
draw_fruits(fruits[km.labels_ == 1])
레이블이 1일때 총 샘플의 개수 98개를 이미지로 출력한 것이다. 레이블이 1일때는 바나나를 의미하는 것같다. 이 클러스터는 모두 바나나로 올바르게 모인 것을 볼 수 있다.
#레이블이 2일때 출력
draw_fruits(fruits[km.labels_ == 2])
레이블이 2인 클러스터는 사과로만 이루어진 것을 볼 수 있다.
레이블이 0일때 조금 섞인 것이 있긴 했지만 학습용 데이터에 타깃 데이터를 전혀 제공하지 않았음에도 스스로 비슷한 샘플을 아주 적절하게 모은 것 같다.
클러스터 중심
KMeans 클래스가 최종적으로 찾은 클러스터 중심은 cluster_centers 속성에 저장되어 있다. 이 배열을 이미지로 출력하고 싶다면 100 X 100의 2차원 배열로 바꾸어야 한다.
draw_fruits(km.cluster_centers_.reshape(-1, 100, 100), ratio=3)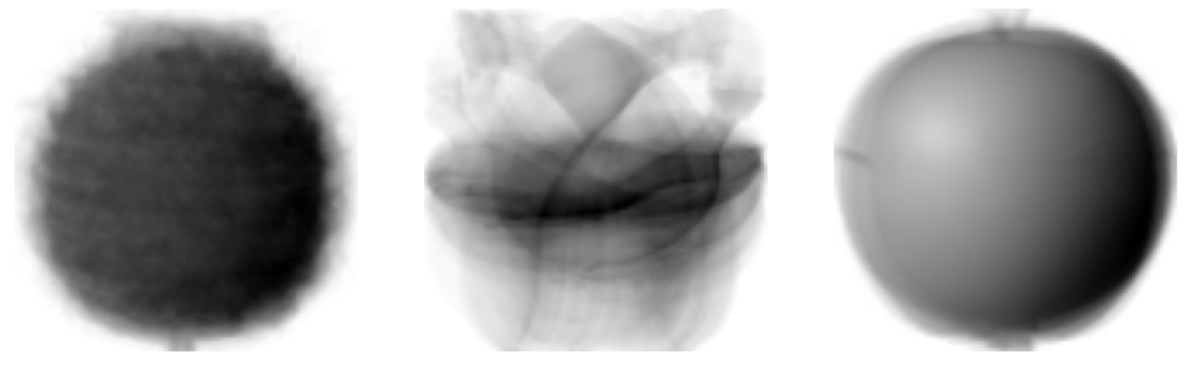
KMeans 클래스는 반복적으로 클러스터 중심을 옮기면서 최적의 클러스터를 찾는다. 알고리즘이 반복한 횟수는 KMeans 클래스의 n_iters 속성에 저장된다.
print(km.n_iter_)
#출력값: 4이번에 우리는 타깃값을 전혀 사용하지 않았지만, 해당 데이터에 사과, 바나나, 파인애플이라는 레이블이 있음을 알기에 n_cluster을 3으로 지정하였다. 이것은 마치 타깃에 대한 정보를 활용한 것이다.
실전에서는 클러스터 개수조차 알 수 없다. 그렇다면 n_cluster이란 값을 어떻게 지정해야 하는 것일까? 과연 최적의 클러스터 개수는 몇일까?
최적의 k 찾기
k-평균 알고리즘의 단점 중 하나는 클러스터 개수를 사전에 지정해야 한다는 것이다. 실전에서는 몇개의 클러스터가 있는지 알 수 없다. 어떻게 하면 적절한 k값을 찾을 수 있는지 알아보자.
가장 대표적인 방법은 엘보우(elbow)이다. k-평균 알고리즘은 클러스터 중심과 클러스터에 속한 샘플 사이의 거리를 잴 수 있다. 이 거리의 제곱의 합을 이너셔(inertia)라 한다. 이녀서는 클러스터에 속한 샘플이 얼마나 가깝게 모여있는지를 나타내는 값이다. 일반적으로 클러스터 개수가 늘어나면 클러스터 개개의 크기는 줄어들기 때문에 이너셔도 줄어든다.
엘보우 방법은 클러스터 개수를 늘려가면서 이녀서의 변화를 관찰하여 최적의 클러스터를 찾는 방법이다.
클러스터 개수를 증가시키면서 이너셔를 그래프로 그리면 감소하는 속도가 꺾이는 지점이 있다. 이 지점부터는 클러스터 개수를 늘려도 클러스터에 잘 밀집된 정도가 크게 개선되지 않는다. 즉 이너셔가 크게 줄어들지 않는다. 이 지점이 마치 팔꿈치 모양이어서 엘보우(elbow) 방법이라고 부른다.
KMeans 클래스는 자동으로 이너셔를 계산해서 inertia_ 속성으로 제공한다. 다음 코드는 클러스터 개수 k를 2~6까지 바꿔가며 학습시킨 후 이너셔값을 리스트에 추가한다. 마지막으로 리스트에 저장된 이너셔 값을 그래프로 출력한다
inertia = []
for k in range(2, 7):
km = KMeans(n_clusters=k, random_state=42)
km.fit(fruits_2d)
inertia.append(km.inertia_)
plt.plot(range(2, 7), inertia)
plt.xlabel('K 개수')
plt.ylabel('inertia')
plt.show()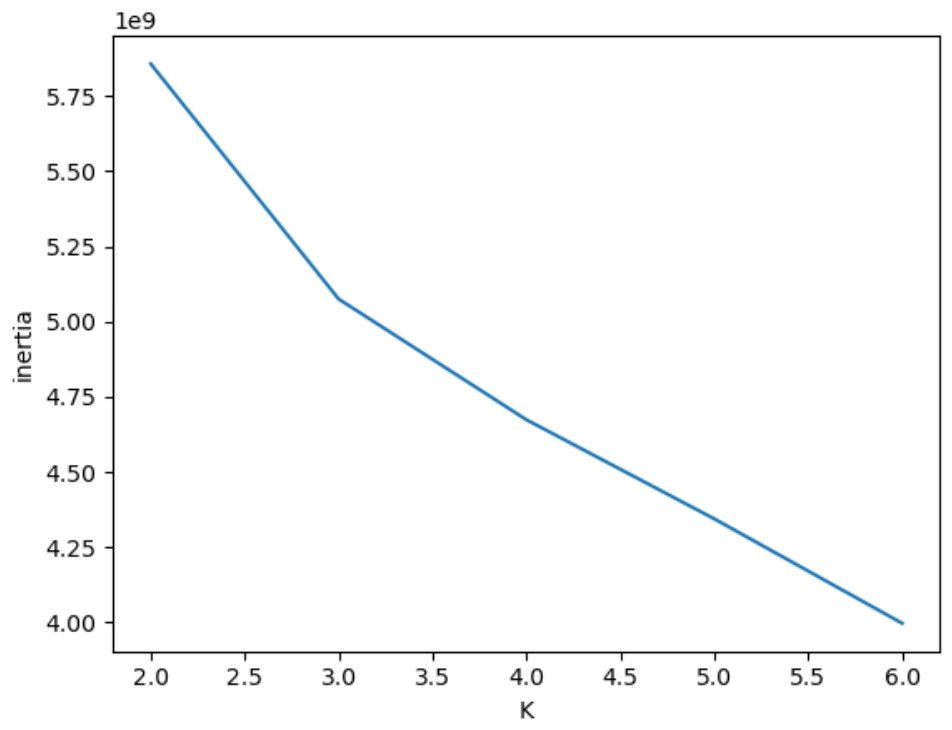
이 그래프는 꺾이는 지점이 뚜렷하지는 않지만 k=3에서 그래프의 기울기가 조금 바뀐 것을 볼 수 있다. 엘보우 지점보다 클러스터 개수가 많아지면 이너셔의 변화가 줄어들면서 군집효과도 줄어든다.
