주성분 분석(PCA)

과일 사진 이벤트를 위하여 고객들이 보낸 여러 개의 이미지를 받아 k-평균 알고리즘으로 분류 후 폴더별로 저장한다. 그런데 너무 많은 사진이 등록되어 저장 공간이 부족하다. 나중에 군집이나 분류에 영향을 끼치지 않으면서 업로드된 사진의 용량을 줄일 수 있을까?

차원과 차원 축소

지금까지 우리는 데이터가 가진 속성을 특성이라 불렀다. 과일 사진의 경우 10,000개의 픽셀이 있기 때문에 10,000개의 특성이 있는 셈이다. 머신러닝에서는 이러한 특성을 차원(Demension)이라 한다. 즉, 10,000개의 특성은 결국 10,000개의 차원이라는 것인데 이 차원을 줄일 수 있다면 저장 공간도 크게 절약할 수 있을 것 같다.

이를 위하여 비지도 학습 작업 중 하나인 차원 축소(Demensionality Reduction) 알고리즘을 다루어 보겠다.

특성이 많으면 선형 모델의 성능이 높아지고 학습용 데이터에 쉽게 과대적합된다. 차원 축소는 데이터를 가장 잘 나타내는 일부 특성을 선택하여 데이터 크기를 줄이고 지도 학습 모델의 성능을 향상시킬 수 있는 방법이다.

또한 줄어든 차원에서 다시 원본 차원으로 손실을 최대한 줄이면서 복원할 수 있다. 이번에는 대표적인 차원 축소 알고리즘인 주성분 분석(Principal Component Analysis)를 배우겠다.

---

주성분 분석 소개

주성분 분석(PCA) 는 데이터에 있는 분산이 큰 방향을 찾는 것으로 이해할 수 있다. 분산은 데이터가 멀리 퍼져있는 정도를 말한다. 분산이 큰 방향이란 데이터를 잘 표현하는 어떤 벡터라고 생각할 수 있다. 다음의 2차원 데이터를 보자.

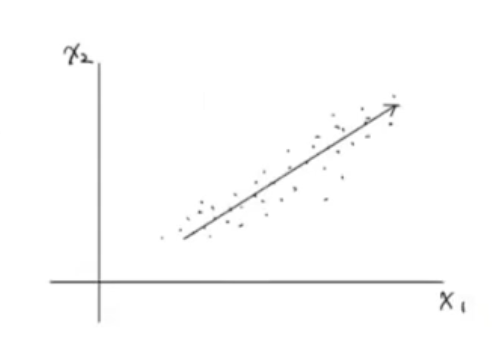
이 데이터에는 x1, x2 2개의 특성이 있다. 대각선 방향으로 길게 늘어진 형태를 가지고 있다. 이 데이터에서 가장 분산이 큰 방향은 어디일까? 즉 가장 데이터의 분폴르 가장 잘 표현하는 방향을 찾아보자.

우리는 직관적으로 길게 늘어진 대각선 방향이 분산이 가장 크다는 것을 알 수 있다. 화살표 위치는 큰 의미가 없다. 오른쪽 위로 향하거나 왼쪽 아래로 향할 수도 있다. 중요한 것은 분산이 큰 방향을 찾는 것이 중요하다.

직선이 원점에서 출발한다면 두 원소로 이루어진 벡터로 쓸 수 있다. 예를들어 다음 그림의 (2, 1)처럼 나타낼 수 있다.

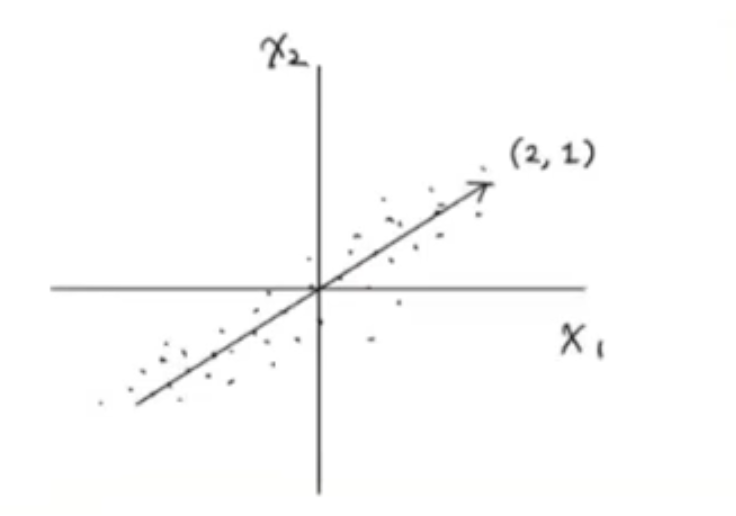
이 벡터를 주성분이라 한다. 이 주성분 벡터는 원본 데이터에 있는 어떤 방향이다. 따라서 주성분 벡터의 원소 개수는 원본 데이터셋에 있는 특성의 개수와 같다. 하지만 원본 데이터는 주성분을 사용해 차원을 줄일 수 있다.

예를 들면 다음과 같이 샘플 데이터 s(4, 2)를 주성분에 직각으로 투영하면 1차원 데이터 p(4, 5)를 만들 수 있다.

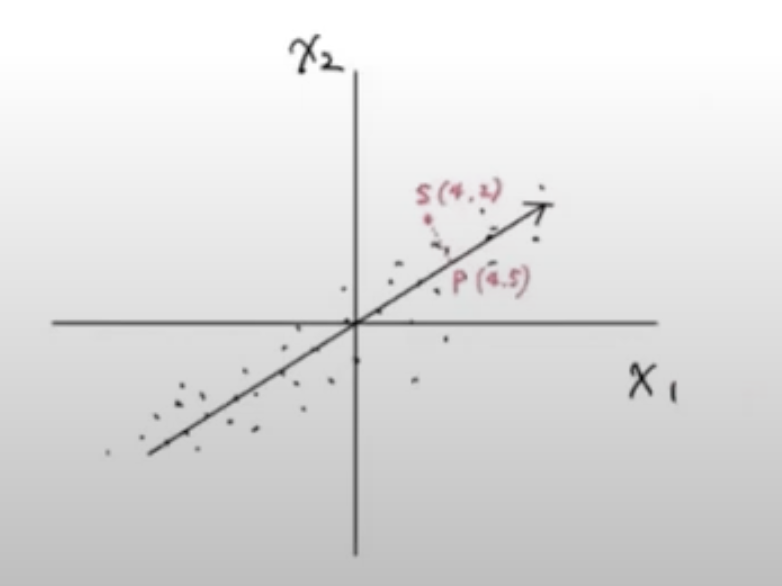
주성분은 원본 차원과 같고 주성분으로 바꾼 데이터는 차원이 줄어든다는 점을 기억하자.

첫 번째 주성분을 찾은 다음, 이 벡터에 수직이며 분산이 가장 큰 다음 방향을 찾는다. 이 벡터가 두 번째 주성분이 된다. 여기에서는 2차원이기 때문에 주성분의 방향은 다음처럼 하나뿐이다.

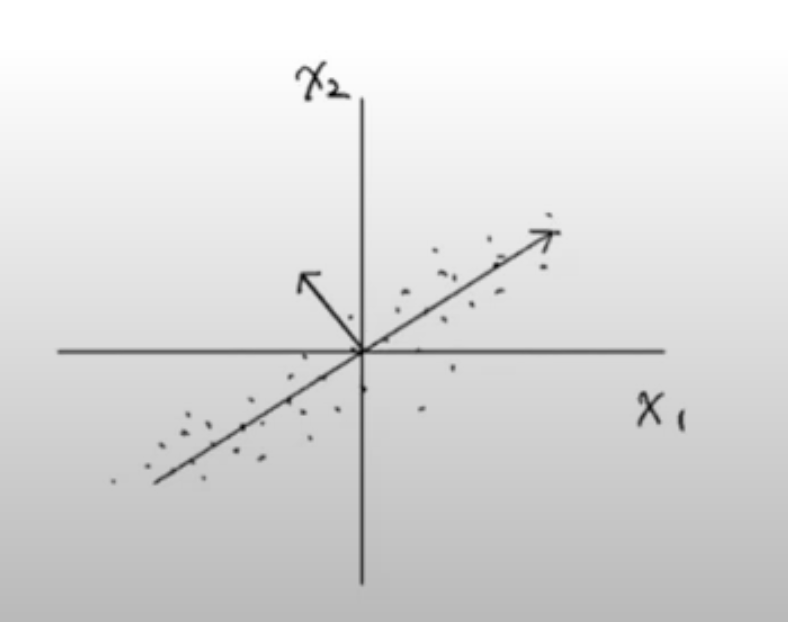
일반적으로 주성분은 원본 특성의 개수만큼 찾을 수 있다.

데이터 준비하기

!wget https://bit.ly/fruits_300_data -O fruits_300.npy

import numpy as np
import matplotlib.pyplot as plt

fruits = np.load('fruits_300.npy')
fruits_2d = fruits.reshape(-1, 100*100)

from sklearn.decomposition import PCA

pca = PCA(n_components=50)
pca.fit(fruits_2d)

print(pca.components_.shape)
#출력값: (50, 10000)

n_components=50으로 설정했기 때문에 pca.components의 첫 번째 차원은 50이다. 두 번째 차원은 항상 원본 데이터의 특성과 같은 10,000개이다.

원본 데이터와 차원이 같으므로, 주성분을 100 X 100 크기의 이미지처럼 출력할 수 있다.

import matplotlib.pyplot as plt

def draw_fruits(arr, ratio=1):
    n = len(arr) #n은 샘플의 개수
    rows = int(np.ceil(n/10))

    #행의 개수가 1개면 열의 개수는 샘플의 개수, 행이 2개 이상이면 열은 10개로 고정
    cols = n if rows < 2 else 10 
    
    #subplot 설정
    fig, axes = plt.subplots(rows, cols, figsize=(cols*ratio, rows*ratio), squeeze=False)

    for i in range(rows): #행마다
        for j in range(cols):  #열마다
            if i * 10 + j < n:   
                axes[i, j].imshow(arr[i*10 + j], cmap='gray_r')
            axes[i, j].axis('off')
    
    plt.show()

draw_fruits(pca.components_.reshape(-1, 100, 100))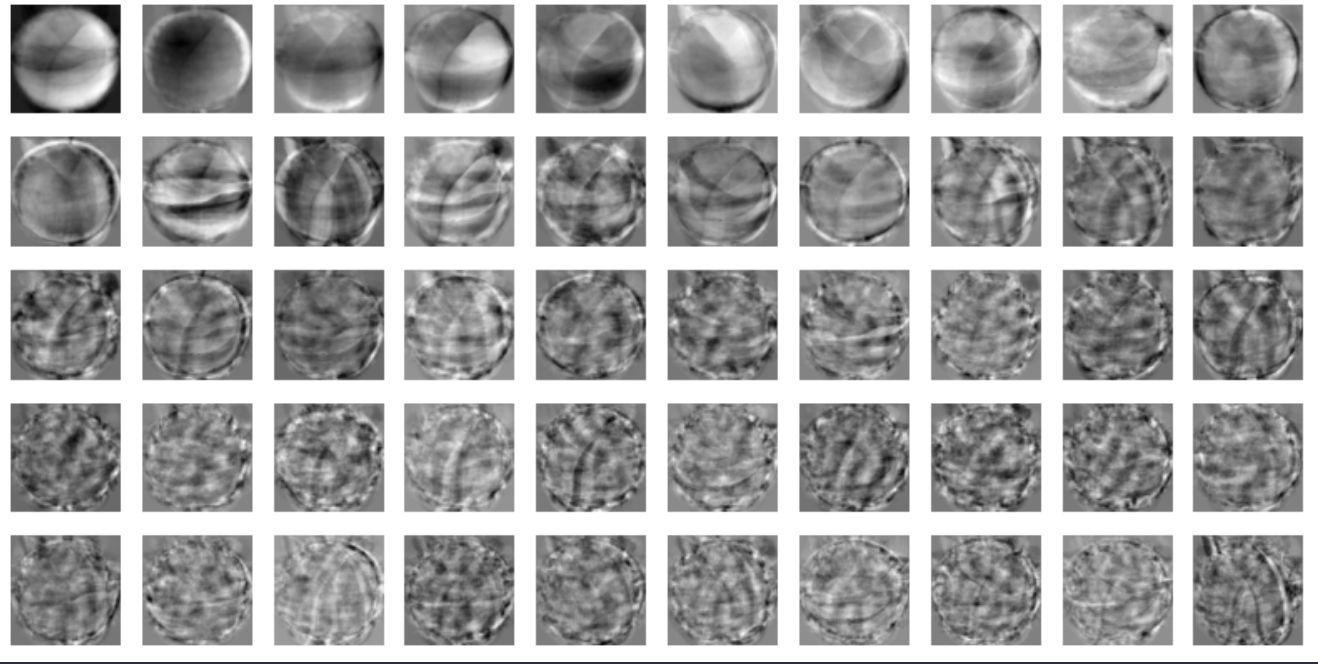

이 주성분은 원본 데이터에서 가장 분산이 큰 방향을 순서대로 나타낸 것이다. 주성분을 찾았으므로 원본 데이터를 주성분에 투영하여 특성의 개수릴 10,000개에서 50개로 줄일 수 있다. 이는 마치 원본 데이터를 각 주성분으로 분해하는 것으로 볼 수 있다.

PCA의 transform() 메서드를 이용해 원본 데이터의 차원을 50으로 줄여보자.