Are Transformers Effective for Time Series Forecasting? (zeng et al., 2022)

일부 Long-Sequence Time Series Forecasting에서 SOTA를 달성한 Dlinear 논문에 대한 리뷰입니다.

Transformer 기반의 모델들이 시계열 예측 문제에서도 다수 제안되고 있는 것에 대해 '과연 Transformer 기반의 모델이 Time Series Forecasting에 적절한가?'라는 본질적 질문을 던지며 매우 간단한 선형 모델로 일부 데이터셋에서 SOTA를 달성하는 흥미로운 논문입니다.

아직 학부생이기에 부족할 수 있지만 최대한 논문의 모든 내용을 세세하게 읽고 리뷰하고자 하였습니다. 감사합니다 :)

📖 Paper : https://arxiv.org/pdf/2205.13504v2.pdf

💻 Github : https://github.com/cure-lab/DLinear

🛠️ My Implementation : (추후 게시 예정)

Abstract

최근 들어 Time Series Forecasting(TSF), 특히 Long Term TSF에서 Transformer 기반의 모델이 다수 제안되고 있습니다. Transformer 기반의 모델은 주로 Self-Attention Mechanism에 기반하고 있는데, 이는 Paired Element 사이에 존재하는 상관관계를 추출하는 것에 뛰어나지만, 'Permutation-Invariant' 즉 순서를 고려하지 않는다는 단점이 있습니다. 시계열 예측 문제의 경우 연속적인 순서로 이루어진 데이터로부터 Temporal Dynamics를 포착하는 것이 매우 중요한 바, Transformer 기반의 모델이 Long-Term TSF 문제에 적합한지에 대해 다시 생각해볼 필요가 있습니다.

본 연구에서는 Transformer를 TSF 문제에 사용하는 적합성에 대해 본질적으로 고민합니다. 대부분의 Transformer 기반의 모델을 제안하는 논문에서 그들이 마치 Non-Transformer 모델에 비해 성능이 좋은 것처럼 표현되고 있으나, 그들이 비교하였던 Non-Transformer 모델은 autoregressive한 방식으로 실험을 진행하였기 때문에 'Error Accumulation Effect'로 인하여 Long-Term 예측에서 성능이 안좋을 수 밖에 없습니다.

따라서 본 연구에서는 놀랍도록 간단한 🔥DLinear🔥라는 모델을 제안하고 성능을 실험하였습니다. 입력을 Trend와 Remainder로 분해하는 부분과 2개의 1-layer network로 구성된 간단한 모델이지만 대부분의 벤치마크에서 Transformer 기반의 모델들보다 성능이 좋았습니다. 우리는 이 연구가 전반적인 시계열 데이터 분석 작업(Anomaly Detection, Time Series Classification)에서 Transformer의 효용성에 대해 다시 생각해 보도록 하는데 도움이 되기를 바랍니다.

1. Introduction

지난 몇십년 동안 TSF 문제는 엄청난 방법론의 진보를 이루었습니다. 순서 개괄은 다음과 같습니다.

(1) 전통적인 통계학 기반 방법론 : ARIMA, SARIMA, ...
(2) 머신 러닝 기법 : Gradient Boosting Regression Tree
(3) RNN 기반 딥러닝 기법 : RNN, LSTM, GRU
(4) CNN 기반 딥러닝 기법 : TCN
(5) Transformer 기반 모델

그 중 Transformer 기반 모델은 가장 성공적인 시퀀스 모델링 구조이며, 자연어 처리나, 음성 인식, 모션 분석 분야에서 비교할 수 없는 성능을 보였으며 최근에는 TSF 문제에 Transformer 기반의 모델을 제안하는 것이 주요 학회에 다수 선정되기도 하였습니다.

• LogTrans (NeurIPS, 2019)
• Informer (AAAI, 2021 Best Paper)
• Autoformer (NeurIPS, 2021)
• Pyraformer (ICLR, 2022 Oral)
• FEDformer (ICML, 2022)

최근 들어 등장한 위와 같은 Transformer 기반의 모델들은 Long-Term Time Series Forecasting에서 기존의 Non-Transformer 기반의 방법론에 비해 정확도 측면에서 Outperform 하고 있는 것처럼 증명되었지만 그들의 실험에서 기존 베이스라인 모델들은 Autoregressive한 방식으로 예측하였으며, 이는 Error Accumulation Effect를 잠재적으로 가지고 있기에 성능이 좋지 않을 수 밖에 없습니다.

더욱이, Transformer 구조의 경우 그 핵심이 Multi-Head Self Attention에 있으며 이 구조의 경우 긴 시퀀스 속의 'Paired Element' 사이에 존재하는 잠재적인 상관관계를 추출하는데는 좋은 성능을 보이지만, 이러한 과정이 'Permutation-Invariant', 즉 시간 순서를 고려하지 않는 점은 간과하고 있습니다. 시계열 데이터 분석의 경우 연속적인 지점 사이에 존재하는 Temporal Dynamics를 발견하기 위해서 입력 데이터의 순서 그 자체도 매우 중요한 역할을 하기 때문에 Multi-Head Self Attention의 동작 원리를 구체적으로 고려해보면 아래와 같은 질문을 할 수 밖에 없습니다.

💡 과연 Transformer가 LTSF(Long Term Time Series Forecasting) 문제를 해결하는데 적절한 것이 맞는가?

본 논문에서는 Transformer 기반의 모델에서 Lookback Window의 크기를 증가시킬수록 예측 오류가 감소되어야하나 그렇지 않은 현상, 심지어 Lookback Window의 크기를 증가시켰음에도 예측 오류가 오히려 증가하는 현상을 지적하고, Transformer와 같이 복잡한 모델을 사용하지 않고 단순히 2개의 1-Layer Linear Network만을 사용하는 모델을 제안하여 여러 LTSF 벤치마크 데이터셋에서 제안한 모델이 아웃퍼폼하는 것을 보이고자 합니다.

---

2. Transformer-Based LTSF Solutions

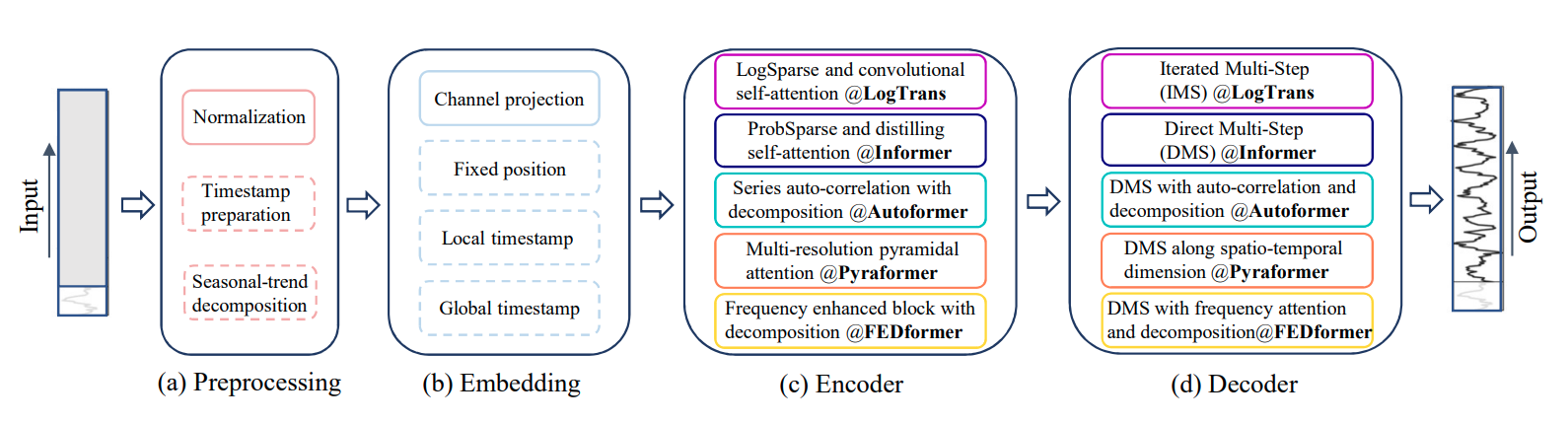
Transformer 기반의 모델들은 자연어처리나 컴퓨터 비전 분야에서 효율성과 성능 개선 측면에서 비교할 수 없는 입지를 가지고 있습니다. 이 때문에 많은 연구자들이 시계열 예측 문제에도 Transformer를 도입하고자 했습니다.

그러나 Vanilla Transformer를 LTSF 문제에 적용할 때 높은 계산/메모리 복잡도와 Autoregressive한 Decoder 구조로 인한 'Error Accumulation' 문제가 존재하며 다양한 Transformer 기반 모델에서 이를 해결하고자 여러 방법을 제안하였습니다.

📌 문제를 해결하는 방법론을 정리하면 아래와 같습니다:

1. Time Series Decomposition :
Input Sequence에 Moving Average Kernel을 적용하여 Trend와 Seasonal 요소로 분해하는 기법입니다. 대표적으로 Autoformer, FEDformer에서 다양한 크기의 Kernel을 통해 시계열 분해 구조를 도입하였습니다.

2. Input Embedding Strategies :
Transformer의 Self-Attention Layer는 시계열 데이터의 Positional Information을 보존하지 못하는 바(Positional Encoding이 수반되는 이유), 시계열 데이터의 Temporal Context를 유지하기 위해서 임베딩이 정말 중요합니다. 여러 모델에서 week, month, year과 같은 hierarchical timestamps나, holidays, events와 같은 agnostic timestamps를 담고 있는 temporal information을 담고자 다양한 임베딩 방법을 도입하였습니다.

3. Self-Attention Schemes :
Transformer는 Paired Element 사이에 존재하는 Semantic Dependency를 추출하기 위해서 Self-Attention Mechanism을 사용하는데, 바닐라 모델의 경우 연산이 n^2로 굉장히 큽니다. 이를 개선하기 위해서 Informer에서 Sparse Attention을 사용하거나 Pyraformer에서 Pyramidal Attention을 사용하는 방식을 제안하였습니다.

4. Decoder :
Vanilla 모델의 경우 Decoder에서 Autoregressive manner에 따라 시퀀스가 나오기 때문에 LTSF에 대해 느린 연산 속도와 Error Accumulation 효과를 가지게 됩니다. 따라서 여러 모델에서 Decoder 대신 FC Layer를 사용하거나 개별적인 Decompostion Scheme을 사용하는 방식으로 이 문제를 해결하였습니다.

앞서 말씀드린 것처럼 Transformer 모델의 전제가 "Semantic Correlation between Paired Element" 이나, 주로 사용하는 Numerical Time Series Data(e.g. stock price, electricity values)는 point들 사이에 semantic correlation이 거의 존재하지 않습니다. 오히려 이와 같은 데이터들에서는 element 사이의 paired relationship보다 오히려 element 사이의 순서가 더 중요한 역할을 하는 것으로 판단됩니다. Transformer에서 Positional-Encoding을 하거나 토큰을 사용하여 임베딩하는 방식으로 순서 정보를 보존한다고 하더라도 Permutation-Invariant Self Attention Mechanism 그 자체가 본질적으로 Temporal Information Loss를 초래하는 것입니다. 그렇기 때문에 본 논문에서는 🚫LTSF의 해결책으로 Transformer 구조를 사용해서는 안된다🚫고 주장하는 바입니다.

---

3. DLinear

본 논문에서는 놀랍도록 간단한 선형 모델인 DLinear을 제안하며, 이렇게 간단한 모델을 제안하게 된 관점 두가지를 다음과 같이 설명합니다.

(1) 1-Layer Linear Network는 미래를 예측하기 위해 과거의 정보를 압축할 수 있는 가장 간단한 모델입니다.

(2) 선행 연구들의 실험을 통해 시계열 분해가 TSF 문제에서 Transformer 기반 모델들의 성능을 높일 수 있는 방법임을 확인할 수 있었으며 Model-Agnostic하고 다른 모델에도 쉽게 적용할 수 있다는 점에서 선형 모델에 적용 가능합니다.

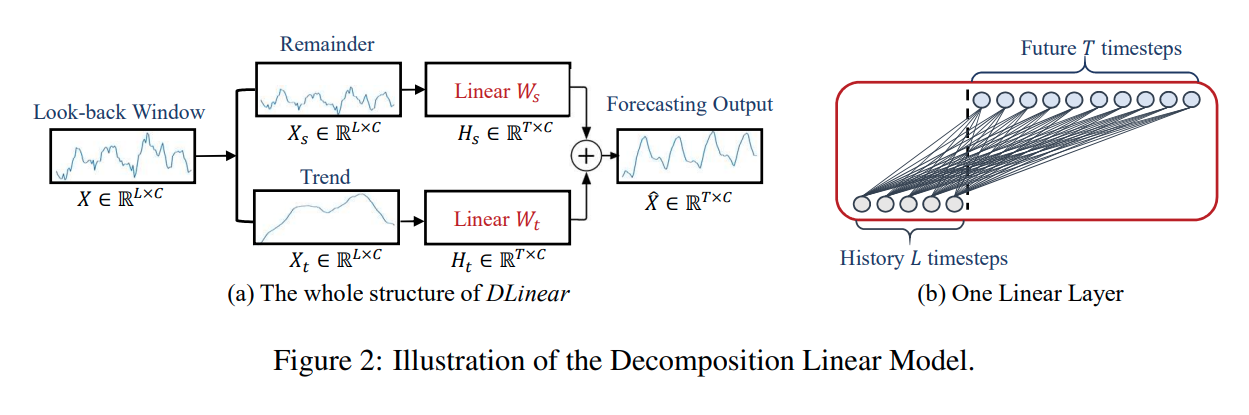
이에 따라 DLinear은 분해 부분과 선형 네트워크로 구성되어 있으며, 이 모델은 시계열 데이터를 Trend Component $X_t$와 Remainder Component $X_s = X - X_t$로 분해한 이후 두개의 1-Layer Linear Network를 적용하는 매우 간단한 구조입니다.

✒️ 그림으로 표현하면 아래와 같습니다.

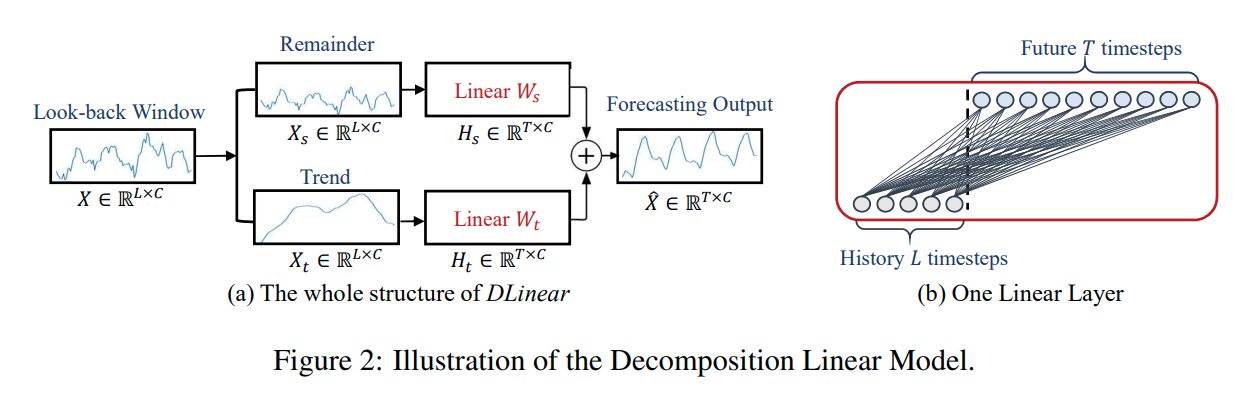
📝 이를 수식으로 표현하면 다음과 같습니다.

(1) $\hat X = H_s +H_t$
(2) Remainder $H_s = W_s X_s$
(3) Trend $H_t = W_t X_t$

전체적으로 예측하고자 하는 $\hat X$는 $H_s$와 $H_t$의 합으로 표현되며, 각각의 $H$는 Weight $W$와 분해된 입력 $X$가 곱해진 형태입니다.

당연하게도 만약에 데이터셋를 구성하는 Variate가 다른 주기성과 다른 트렌드를 가지고 있다면 다른 Variate 사이에 Weight를 공유하는 DLinear의 경우 성능이 좋지 못할 것이기 때문에 두가지 디자인의 DLinear을 제안합니다. 우리는 모든 Variate가 같은 Linear Layer를 공유하는 형태를 DLinear-S라 하고, 각각의 Variate가 각기 다른 Linear Layer를 가지는 형태를 DLinear-I라고 하였으며, 기본적으로는 DLinear-S를 사용하였습니다.

비록 DLinear의 구조 자체는 매우 간단하지만 이 모델이 가지는 장점은 꽤 많습니다.

• O(1) Traversing Path Length : Short Range와 Long Range의 Temporal Relation을 낮은 연산량으로 포착할 수 있습니다.
• Hight Efficiency : Transformer에 비해 사용 메모리와 파라미터가 적기 때문에 연산 속도가 더 빠릅니다.
• Interpretability : Seasonality와 Trend에 대한 Weight가 분해된 Input에 곱해진 선형 모델이기 때문에 Weight에 대한 분석을 통해 직관적인 해석이 가능합니다.
• Easy to use : Transformer와 달리 하이퍼파라미터 튜닝 없이 사용 가능합니다.

---

Implementation

DLinear을 다음과 같이 구현할 수 있습니다.

(1) 우선 입력 시계열 데이터를 Trend와 Seasonality로 분해하는 부분이 필요합니다.

# 시계열 데이터를 분해하는 부분
class moving_avg(nn.Module):
    """
    Moving average block to highlight the trend of time series
    """
    def __init__(self, kernel_size, stride):
        super(moving_avg, self).__init__()
        self.kernel_size = kernel_size
        self.avg = nn.AvgPool1d(kernel_size=kernel_size, stride=stride, padding=0)

    def forward(self, x):
        # padding on the both ends of time series
        front = x[:, 0:1, :].repeat(1, (self.kernel_size - 1) // 2, 1)
        end = x[:, -1:, :].repeat(1, (self.kernel_size - 1) // 2, 1)
        x = torch.cat([front, x, end], dim=1)
        x = self.avg(x.permute(0, 2, 1))
        x = x.permute(0, 2, 1)
        return x


class series_decomp(nn.Module):
    """
    Series decomposition block
    """
    def __init__(self, kernel_size):
        super(series_decomp, self).__init__()
        self.moving_avg = moving_avg(kernel_size, stride=1)

    def forward(self, x):
        moving_mean = self.moving_avg(x)
        res = x - moving_mean
        return res, moving_mean

(2) 분해된 입력을 각각 1-Layer Linear Network에 통과시켜 예측 결과를 얻는 모델을 구현합니다.

# 1-layer linear network 구현 부분
class Model(nn.Module):
    """
    DLinear
    """
    def __init__(self, configs):
        super(Model, self).__init__()
        self.seq_len = configs.seq_len
        self.pred_len = configs.pred_len

        # Decompsition Kernel Size
        kernel_size = 25
        self.decompsition = series_decomp(kernel_size)
        self.individual = configs.individual
        self.channels = configs.enc_in

        if self.individual:
            self.Linear_Seasonal = nn.ModuleList()
            self.Linear_Trend = nn.ModuleList()
            self.Linear_Decoder = nn.ModuleList()
            for i in range(self.channels):
                self.Linear_Seasonal.append(nn.Linear(self.seq_len,self.pred_len))
                self.Linear_Seasonal[i].weight = nn.Parameter((1/self.seq_len)*torch.ones([self.pred_len,self.seq_len]))
                self.Linear_Trend.append(nn.Linear(self.seq_len,self.pred_len))
                self.Linear_Trend[i].weight = nn.Parameter((1/self.seq_len)*torch.ones([self.pred_len,self.seq_len]))
                self.Linear_Decoder.append(nn.Linear(self.seq_len,self.pred_len))
        else:
            self.Linear_Seasonal = nn.Linear(self.seq_len,self.pred_len)
            self.Linear_Trend = nn.Linear(self.seq_len,self.pred_len)
            self.Linear_Decoder = nn.Linear(self.seq_len,self.pred_len)
            self.Linear_Seasonal.weight = nn.Parameter((1/self.seq_len)*torch.ones([self.pred_len,self.seq_len]))
            self.Linear_Trend.weight = nn.Parameter((1/self.seq_len)*torch.ones([self.pred_len,self.seq_len]))

    def forward(self, x):
        # x: [Batch, Input length, Channel]
        seasonal_init, trend_init = self.decompsition(x)
        seasonal_init, trend_init = seasonal_init.permute(0,2,1), trend_init.permute(0,2,1)
        if self.individual:
            seasonal_output = torch.zeros([seasonal_init.size(0),seasonal_init.size(1),self.pred_len],dtype=seasonal_init.dtype).to(seasonal_init.device)
            trend_output = torch.zeros([trend_init.size(0),trend_init.size(1),self.pred_len],dtype=trend_init.dtype).to(trend_init.device)
            for i in range(self.channels):
                seasonal_output[:,i,:] = self.Linear_Seasonal[i](seasonal_init[:,i,:])
                trend_output[:,i,:] = self.Linear_Trend[i](trend_init[:,i,:])
        else:
            seasonal_output = self.Linear_Seasonal(seasonal_init)
            trend_output = self.Linear_Trend(trend_init)

        x = seasonal_output + trend_output
        return x.permute(0,2,1) # to [Batch, Output length, Channel]

---

4. Experiments

Dataset.

- ETT(Electricity Transformer Temperature)
{ETTh1, ETTh2, ETTm1, ETTm2}
- Traffic
- Electricity
- Weather
- ILI
- Exchange Rate

Evaluation Metric.

- MSE
- MAE

Compared Methods.

- FEDformer
- Autoformer
- Informer
- Pyraformer
- LogTrans
- Reformer

실험 결과는 아래와 같습니다.

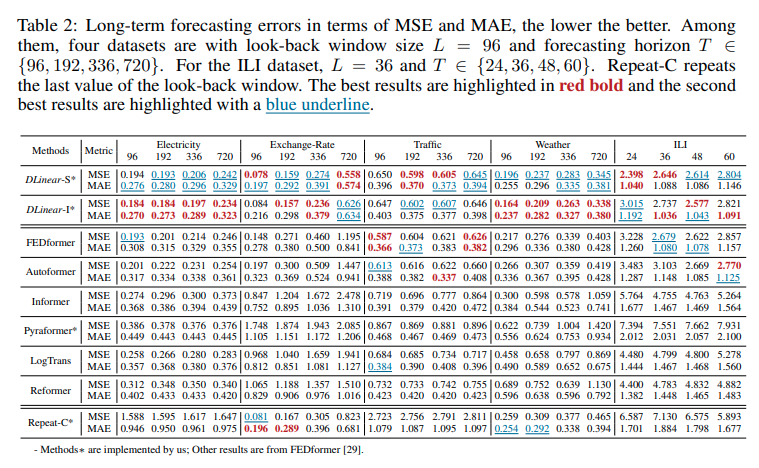
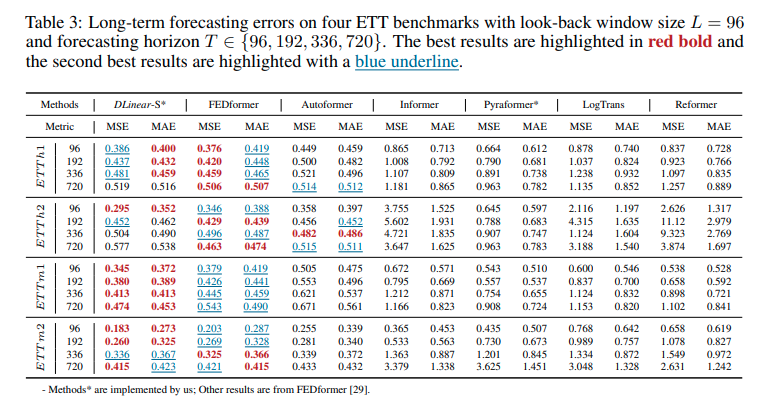
Interpretability?

앞서 언급한 것처럼 DLinear은 다음과 같은 수식으로 표현할 수 있습니다 :
(1) $\hat X = H_s +H_t$
(2) Remainder $H_s = W_s X_s$
(3) Trend $H_t = W_t X_t$

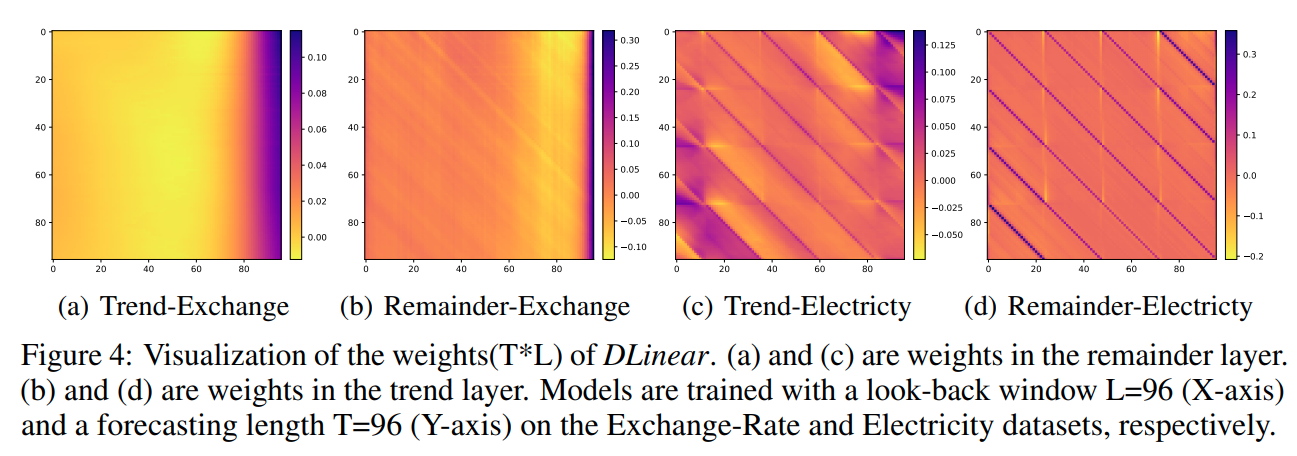
매우 간단한 선형 모델이기 때문에 DLinear의 Weight $W$는 모델이 어떻게 동작하고 있는지에 대한 직관적인 해석을 제공할 수 있습니다.

위 그림의 (a)와 (b)는 Exchange Rate 데이터에 대한 결과입니다. 금융 시계열 데이터의 경우 주기성과 계절성이 거의 존재하지 않기 때문에 일정한 패턴을 보이지는 않지만, Trend Layer를 통해 Output에 가까운 정보들이 높은 Weight를 가지고 있는 것을 보며, 해당 데이터들이 예측값에 많은 기여를 하고 있음을 확인할 수 있습니다.

또한 (c)와 (d)의 경우 Electricity 데이터에 대한 결과로 24step을 주기로 동일한 패턴이 반복되는 것을 볼 수 있는데 이는 해당 데이터가 하루 전력 사용량에 대한 데이터이고, 하루가 24시간 이기 때문입니다.

Method Efficiency?

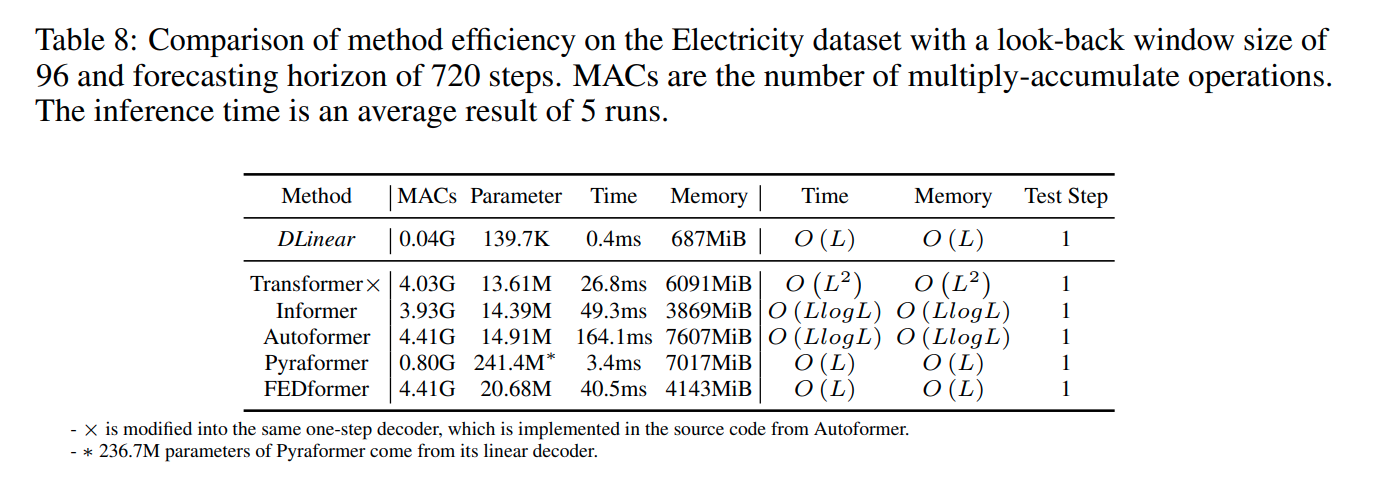
Multiply-Accumulate Operation(MACs), 파라미터의 수, 시간 복잡도와 메모리 측면에서 DLinear은 Transformer 기반의 모델들에 비해 효율적임을 확인할 수 있습니다!

---

5. Conclusion(사견)

최근 주요 학회들에서 Transformer 기반의 모델들이 시계열 예측 문제에 대한 해결 방안으로 발표되었으며 일부는 Best Paper로 채택까지 되었으나, 자연어 처리 분야에서 주로 사용되는 Transformer를 굳이 시계열 예측 문제에 사용하는 것이 효율적인가에 대한 근본적인 질문을 던지는 논문입니다.

2022.05.22일에 발표된 논문이나 많은 주목을 받고 있는 만큼 위의 질문에 대해 생각해 볼 필요가 있다고 판단됩니다.

.
.
.

References

• https://arxiv.org/pdf/2205.13504v2.pdf