Time Series Forecasting에서 가장 SOTA(State of the art) 논문인 TFT입니다.

아직 학부생이기에 부족할 수 있지만 최대한 논문의 모든 내용을 세세하게 읽고 리뷰하고자 하였습니다. 감사합니다 :)

Paper : https://arxiv.org/abs/1912.09363

Github : https://github.com/jdb78/pytorch-forecasting

My Implementation : (추후 게시 예정)

Abstract

여러 날을 예측하는 Multi-Horizon Forecasting 시계열 데이터는 복잡한 입력들을 포함하는데 그러한 것들에는 시간에 따라 변하지 않는 변수(이 논문에서는 Static Covariates라 표현), 시간에 따라 변하는 관측가능한 변수(Time Varying Observable Input), 타겟과 어떠한 상호작용을 하는지 사전 정보가 없는 외인성 변수(Exogenous Variable) 등이 존재합니다.

현재까지 여러 딥러닝 모델들이 제안되었지만, 그들은 대표적인 Black Box 모델들로 실제 상황에서 전체 길이의 입력들이 어떻게 사용되는지, 모델은 어떠한 Time Step을 중요하게 고려하고 있는지에 대한 통찰을 제공하지는 못합니다.

따라서 본 논문에서는 Attention 기반 구조와 해석 가능한 인사이트를 제공할 수 있는 TFT(Temporal Fusion Transformer)를 제안하였습니다.

1. Introduction

미래의 여러 Time Step에 대해서 예측을 진행하는 Multi-Horizon Forecasting은 시계열 예측 분야에서 매우 중요한 문제입니다. 한 스텝 후만 예측하는 것과 달리 Multi-Horizon은 전체 시계열 데이터에 대한 접근을 가능하게 하고, 미래의 다양한 스텝들에 대한 예측 결과를 통해 활용할 수 있는 범위도 넓힐 수 있습니다. 미래에 대한 예측은 유통업, 헬스 케어, 금융 분야에서 중요하게 사용되고 있으며 시계열 예측의 성능 향상은 엄청난 잠재력을 가지고 있다고 볼 수 있습니다.

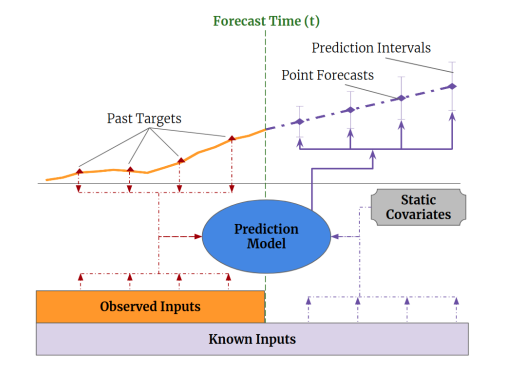
💡 실제 Multi-Horizon Forecasting은 위 그림과 같이 다양한 데이터 Input이 필요합니다.

(1) 현재에는 관측을 통해서 그 값을 알 수 있지만 미래의 값은 알 수 없는 Observed Input
(2) 시간에 따라 달라지지만, 현재에도 그 값을 알 수 있으며 미래에도 그 값을 알 수 있는 Time Vary Known Input(week, weekofyear, holiday, quarter)
(3) 시간과 관계 없이 변하지 않는 정적 공변량 Static Covariates(ex 상점의 위치)

과거에 Autoregressive Model이 사용되었으나, 이는 모든 외인성 입력들이 미래에도 알 수 있다는 가정을 하고 있다는 문제가 있었으며, 많은 모델이 Time-Dependent Feature 들과 단순하게 결합하는 방식으로 동적인 Covariates를 무시했던 등의 이유로 Multi-Horizon의 다양한 종류의 입력들을 고려하는데 실패하였습니다. 최근 많은 개선된 모델들이 데이터의 고유한 특성을 구조적으로 정렬함으로써 좋은 성과를 얻어냈으며, 현재 사용되는 대부분은 모델들은 'Black Box'모델들로 예측이 많은 파라미터 사이에 복잡한 비선형적인 상호작용에 의해 결정하게 됩니다.

모델이 한 예측에 대해서 왜 그런 결과가 나왔는지 이유를 제공해줄 수 없는 이러한 Black Box 모델은 유저들이 모델의 출력을 신뢰하거나 개발자가 모델의 구조를 디버깅하기 힘들게 합니다. 그리고 대부분은 DNN 모델들은 시계열에 적합하지 않다는 한계가 있습니다.

📌 현재까지 사용되던 모델들은 아래와 같은 문제가 있었습니다.
(1) Convolution 기반의 Post-Hoc 기법인 LIME과 SHAP은 Input Feature의 시간 순서를 고려하지 않습니다.

• LIME은 매 데이터 포인트마다 독립적으로 모델들이 만들어지기에 매우 비효율적입니다.
• SHAP의 경우 Feature들이 근접한 Time Step과 독립적으로 고려된다는 점에서 시계열에 적합하지 않습니다.

이러한 Post-Hoc 접근들은 시계열 데이터에서 중요한 시간대에 따른 상관관계를 설명하는 능력이 매우 부족합니다.

(2) 반면 Language나 Speech에서 주로 사용되는 Attention 기반의 모델들은 Sequence 데이터에 대한 해석력이 매우 뛰어나다. Language나 Speech와 달리 시계열 데이터는 다양한 Feature를 가지고 있다는 것이 특징입니다.

이러한 방법론을 시계열 데이터에 적용했을 때 중요한 Time Step을 발견할 수는 있지만 Feature 간의 관계에서 어떤 Feature가 중요하게 고려되고 있는지, 주어진 Time Step에 따른 Feature들의 각각의 중요성을 구분하기는 힘들다는 한계가 있습니다. 따라서 새로운 기법은 이러한 예측이 해석가능하게 하는 것이 필수적일 것입니다.

Attention 기반의 DNN 구조인 TFT는 새로운 해석력을 제공합니다. Attention Score를 통해 Time Step에서의 중요성을 해석할 수 있음은 물론, Static Variable에 대하여, Encoder Variable에 대하여, Decoder Variable에 대해서 Interpretation을 제공한다는 점에서 큰 장점을 가집니다.

2. Related Work

(1) Multi-Horizon Forecasting에 사용되던 DNN

Autoregressive 모델들과 Seq2Seq 모델로 나뉘며 DeepAR과 같은 LSTM Network나 DSSM(Deep State Space Model) 등이 존재합니다. 최근에는 Transformer 기반의 구조들이 예측 시 receptive 영역을 늘리기 위해 지역적인 처리를 하는 convolution이나 sparse attention을 같이 사용하고 있습니다. (Conv-Transforemr, Informer)

과거 사용하던 대부분의 모델은 여러 Horizon에 대한 값을 한번에 출력하도록 훈련되었습니다. 이러한 모델들은 일반적으로 Seq2Seq 모델을 기반으로 하며, LSTM 인코더를 이용하여 과거의 입력을 요약하고 미래의 예측을 다양한 기법을 사용하여 만들어냈습니다. MQRNN(Multi-Horizon Quantile Recurrent Forecaster)는 LSTM이나 Conv 인코더를 이용하여 Context Vector를 만들고 이를 각각의 Horizon에 대하여 MLP에 feed하였습니다. Multi-Model Attention 기법은 LSTM 인코더를 이용하여 Context Vector를 만들고 Bi-directional LSTM을 디코더로 사용하여 이전 기법들에 비해서 좋은 성능을 가지고 있지만 해석력은 여전히 문제가 되었습니다.

TFT는 이러한 문제를 정적 Feature들에 대하여 개별적인 Encoder-Decoder Attention을 사용함으로 해결하고자 하였습니다.

Attention 기법은 번역, 이미지 분류, Tabular Learning 등에서 Attention의 가중치를 이용하여 각각의 입력의 영향력을 알 수 있게 해줍니다. 최근 시계열에서 해석력을 위해 사용하는데 이들은 정적 공변량(Static Covariates)의 중요성은 고려하지 못한다는 한계가 있었습니다.

현재 Attention의 Explanability에 대한 많은 논의가 있지만 이 논문에서는 다루지 않도록 하겠습니다.

TFT의 핵심 아이디어

(개인적인 생각)

위의 그림이 TFT의 핵심 아이디어를 잘 보여준다고 생각합니다. 제가 생각하는 TFT의 핵심은 아래와 같습니다.

• 현재 시점에서 알 수 없는 미래의 관측 변수(Observed Input)과 현재 시점에서 미래 시점의 값을 알 수 있는 변수(Known Input)을 활용하면 Time Series Data에 대한 Prediction 성능을 높일 수 있다!

• 시간에 따라 변하지만 미래 시점의 값을 현재 시점에서도 알 수 있는 변수(Time Varying Known Input)과 시간에 따라 변하지 않는 변수인 정적 공변량(Static Covariates)이 함께 모델에 입력되어 다중 시점에 대한 예측(Multi-Horizon Forecasting) 시 활용될 수 있다!

3. Multi-Horizon Forecasting

주어진 시계열 데이터셋에 대하여 고유한 객체 $I$가 존재한다고 하면, 각 객체 $i$는 정적 공변량의 집합과 연관되어 있습니다. (상점의 경우 I는 고객, 정적 공변량은 상점의 위치가 될 것입니다) 시간에 의존적인 입력 Feature들은 두 개로 나뉘는데 하나는 Observed Input이고 나머지는 Known Input입니다. (위의 핵심 아이디어 부분에서 설명한 바와 같습니다)

여러 상황에서 TFT는 Quantile Regression을 사용하여 예측을 진행하며, 각 Quantile 예측은 다음과 같은 형태를 보이게 됩니다.

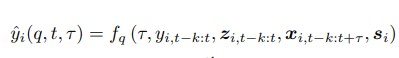
이 때, $y$는 $q$번째 Sample Quantile에 대하여 $t$ 시점에서 $\tau$번째 뒤에 해당하는 예측에 해당하며, $f$는 예측 모델입니다. $k$의 Look-back Window를 이용하여 시작하는 지점인 $t$로부터 $k$개 이전까지의 값들을 이용하는 식이라고 해석할 수 있습니다. $x$는 Known Input, $s$는 Static Covariate의 집합을 의미합니다.

4. Model Architecture

TFT의 모델의 구조는 아래와 같습니다.

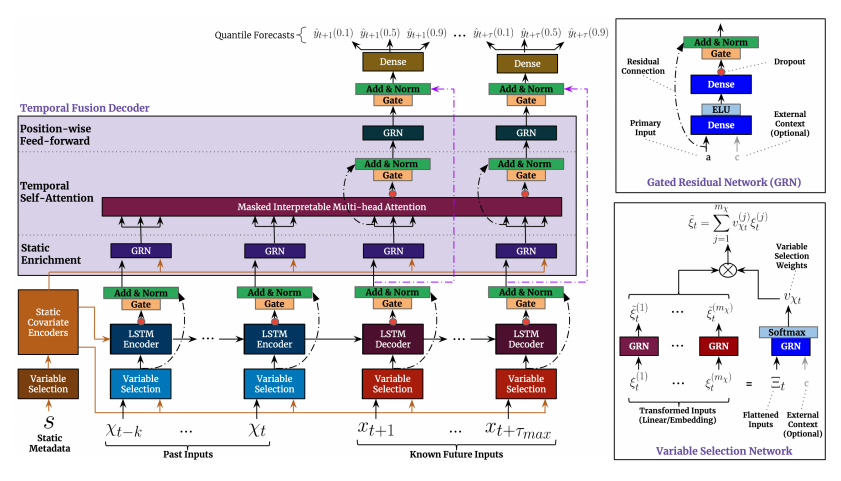
💡 TFT의 주요 구성은 아래와 같습니다.

(1) Gating Mechanism을 통해 불필요한 성분을 스킵하여 광범위한 데이터셋에 대하여 adaptive depth와 network complexity 감소를 통해 가능하게 합니다.

(2) Variable Selection Network를 통해 관련 있는 Input Variable만 선택합니다.

(3) Static Covariate Encoder를 통해 정적 공변량들을 Context Vector에 인코딩하고 네트워크에 결합합니다.

(4) Temporal Processing을 통해 Observed Input과 Known Input 모두에 대해 장기 단기 시간 관계를 학습합니다. Local Processing을 위해 seq2seq layer를 사용하며, Interpretable Multi-Head Attention을 통해 장기 의존성을 알아냅니다.

(5) Prediction Intervals을 통해 Quantile을 이용하여 매 Prediction Horizon에 대하여 Target이 존재할 수 있는 범위를 제공합니다.

4.1 Gating Mechanisms

Exogenous Input과 Target 사이의 관계는 종종 미리 알 수 없어 어떠한 변수들이 연관되어 있는지 예측하기 어렵게 합니다. (ex 금융 데이터를 예시로 들었을 때 코로나의 발생과 Target인 지수 데이터의 관계는 미리 알 수 없어 예측이 어려울 것입니다.) 더욱이 필요되는 비선형 처리의 길이를 결정하기 힘들며 단순한 모델들이 훨씬 효과적일 수 있는 작거나 잡음이 심한 데이터셋이 존재하기도 합니다.

TFT는 필요할 때만 비선형 처리를 하여 모델의 유연성을 높이고자 GRN(Gated Residual Network)를 제안합니다. 초기 입력 a와 선택적 context vector $c$를 받아 아래와 같이 처리합니다.

여기서 ELU는 Exponential Linear Unit Activation Function을 의미하고, $\eta$ 1, 2는 모두 중간 층에 해당하며, $ω$는 Weight Sharing Index를 의미합니다. 그 과정에서 Standard Layer Normalization을 사용하였습니다. ELU는 입력이 0보다 크면 Identify Function으로 동작하며, 0보다 작을 때는 일정한 출력을 내며, GLU(Gated Linear Units)을 사용하여 주어진 데이터셋에서 필요하지 않은 부분을 제거합니다. GLU의 수식은 다음과 같습니다.

시그모이드 함수를 활성화 함수로 사용하였으며 연산은 Elementwise Hadamard Product를 사용합니다. GLU는 TFT에서 Input a의 비선형 기여도를 바꿀 수 있는데 예를 들어 GLU의 출력이 모두 0이라면 비선형 기여도를 suppress하기 위해서 Layer를 Skip하는 것으로 취급합니다. Context Vector가 없다면 GRN은 Context Input을 0으로 취급합니다. (c=0) 학습 과정에서 gating layer와 normalization 이전에 dropout을 적용합니다.

4.2 Variable Selection Networks

다양한 변수들이 사용가능한 반면, 출력에 대해서 그들의 연관성이나 명확한 기여도는 일반적으로 알기 어렵습니다. TFT는 Instance-wise 변수 선택을 통해 (즉 Static Covariate와 Time Dependent Covariate 모두에 대하여) 예측에 직결되는 성분을 골라내는 것은 물론, 불필요한 noisy 입력들을 줄일 수 있습니다. 대부분의 실제 시계열 데이터에는 예측과 관련없는 값들이 많으므로 이와 같은 Variable Selection을 통해 성능을 개선할 수 있습니다.

Categorical Variables에 대해서는 Entity Embedding을, Continuous Variables에 대해서는 Linear Transformation을 진행합니다. 모든 Static Covariates, Past & Future Input들에 대해 분리된 변수 선택 네트워크를 사용합니다. ξ을 각 시점에서의 변형된 입력이라 하고, Ξ를 모든 이전 시점 t에 대한 입력들의 flatten 벡터라 하면, 수식은 아래와 같습니다.

$v_{χt}$가 Variable Selection Weight의 Vector이며, $c$는 Static Covariate Encoder를 통해 얻을 수 있습니다. Static Variable에 대해서 Context Vector $c$는 Static Information을 담고 있다고 볼 수 있습니다.

매 시점마다, GRN을 통해 ξt(j)를 feeding하면서 비선형 처리를 위한 추가적인 Layer를 거치게 됩니다.

$ξt(j)$는 Variable j에 대해 전처리된 Feature Vector이며, 우리는 각자의 GRN에 $ξt(j)$를 넣어줌을 통해 가중치를 모든 시점 $t$에 대해서 공유하는 가중합을 구할 수 있으며 그 식은 아래와 같습니다.

$ξt=\sum_{j=1}^{mχ}{vχt(j)ξt(j)}$

위의 식에서 $vχt(j)$는 Vector $vχt$의 $j$번째 element입니다.

4.3 Static Covariate Encoder

TFT는 정적인 메타데이터의 정보를 통합하기 위해서 설계되었습니다. 따라서 개별적인 GRN 인코더를 이용하여 4개의 서로 다른 Context Vector인 $cs, ce, cc, ch$를 만들게 됩니다. 이들은 Temporal Decoder에서 다양하게 사용되며 자세하게는 $cs$는 시간 변수를 선택하는 context, $cc$와 $ch$는 지역 처리를 위한 시간 변수, $ce$는 정적인 정보들에 대한 시간 변수들을 의미합니다.

예를 들어 $ζ$를 Static Variable Selction의 Output이라고 할 때, Temporal Variable Selction을 위한 Context $cs$는 아래와 같은 식을 통해 구할 수 있습니다.

4.4 Interpretable Multi-Head Attention

TFT는 Self-Attention Mechanism을 통해 다른 시점에 대한 Long-Term Relation을 파악합니다. 구체적으로는 Transformer 기반의 Multi-Head Attention을 통해 해석력을 강화하였습니다. 일반적으로 Attention Mechanism의 Attention은 다음과 같이 계산됩니다.

$A()$는 Normalization Function이며 $N$은 Attention Layer를 통과하는 time step의 개수이며 일반적으로는 Dot-product Attention을 사용합니다.

기본적인 Attention의 Learning Capacity를 개선하기 위해서 Multi-Head Attention을 제안하였으며, 이는 여러 Head에서 각기 다른 Representation Subspace를 사용함으로써 학습 효용성을 개선하는 방식이라고 볼 수 있습니다.

다른 값들이 각각 다른 Head에서 사용되기 때문에 Attention의 가중치가 단독으로는 특정 Feature의 중요성을 나타내는 지표가 되기 어렵습니다. 따라서 다음과 같이 Multi-Head Attention을 수정하여 각 Head에서 값을 공유할 수 있도록 만들었습니다.

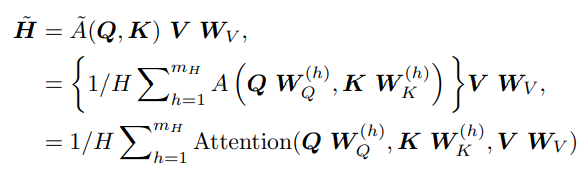
각 Head는 다른 시간 Pattern을 학습하고 이들이 입력으로 단순히 Ensemble 된 것이라고 생각할 수 있습니다. $A(Q,K)$와 비교하였을 때 증가된 Representation Capacity를 제공함은 물론, 하나의 Attention Weight Output을 제공함을 통해 Interpretability를 확보하였습니다.

4.5 Temporal Fusion Decoder

Temporal Fusion Decoder는 데이터셋에 존재하는 시간 간의 관계에 대해서 학습합니다.

4.5.1 Locality Enhancement with seq2seq layer

시계열 데이터에서는 주위 값들 사이의 연관성을 통해 중요도가 결정되곤 합니다. Anomalies, Change-point, Cyclical Pattern 등과 같은 Local Context를 끌어올리는 것은 따라서 Attention 기반 모델에서 성능 향상을 가능하게 합니다.

예를 들어 1개의 Conv 층을 이용하여 모든 시간대에 대하여 동일한 filter를 사용하고, 지역적 패턴을 추출하여 Locality를 추출할 수 있으나 Observed Data가 있는 경우에는 과거와 미래의 입력 숫자가 다르기 때문에 적합하지 않습니다. 이 차이를 해결하기 위해서 $t_{k} ~ t$를 인코더에 넣어 Context Vector를 생성하고 $t+1 ~ t+t_{max}$를 디코더에 넣어줍니다.

TFT에서는 LSTM 인코더와 디코더를 사용하였으며, 다른 모델 역시 사용할 수는 있습니다. 이와 같은 인코더 디코더는 Positional 인코딩을 대신하는 효과도 있는데 시간 순서에 대한 적절한 Inductive Bias를 제공해주기 때문입니다. 추가적으로 Static Meta Data를 활용하기 위해 $cc$와 $ch$와 같은 context vector를 사용하는데 이는 Cell State와 Hidden State의 초기값이 됩니다. 아래와 같이 수식을 표현할 수 있습니다.

위의 식에서 $n$은 Position Index를 의미합니다.

4.5.2 Static Enrichment Layer

Static Covariates는 Temporal Dynamics에서 큰 영향을 미칠 수 있습니다. (ex 특정 유전자의 질병 발생률에의 영향) 따라서 TFT는 Static Enrichment 층을 이용하여 이러한 Static 메타 데이터의 사간 Feature를 강화합니다. 각 위치 $n$에 대하여 아래와 같습니다.

$GRNθ$는 전체 Layer에서 공유되는 Weights이며, $c_{e}$는 Static Covariate Encoder를 통해 나온 Context Vector입니다.

4.5.3 Temporal Self-Attention Layer

Static Enrichment에 이어서 Self-Attention을 적용합니다. 모든 Static Enriched된 시계열 Feature들은 하나의 Matrix로 그룹화 됩니다.

위와 같이 그룹화되며 이후에 Interpretable Multi-Head Attention을 모든 예측하고자 하는 Time Step에 적용합니다. 수식은 아래와 같습니다.

Decoder Masking이 Multi-Head Attention에 적용되는데, 각각의 Temporal Dimension이 그에 해당하는 Feature에 상응할 수 있도록하기 위함입니다. Self-Attention Layer는 TFT가 RNN으로는 잡아내기 어려운 Long-Range Dependency에 대하여 잡아낼 수 있도록 함은 물론, 추가적인 Gating Layer를 통해 학습을 촉진시킵니다.

4.5.4 Position-Wise Feed-Forward Layer

Self-Attention Layer에 추가적인 비선형 처리를 합니다. Static Enrichment Layer와 유사하게 아래와 같이 GRN을 사용합니다.

전과 마찬가지로 $GRNψ$의 Weight는 모든 Layer에 공유되며, Gated Residual Connection을 통해 전체 Transformer Block을 모두 Skip할 수 있도록 하였습니다.

4.6 Quantile Outputs

예측하고자 하는 Time Step에 대해 다양한 Percentage 범위의 Output을 제공합니다.

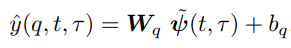
5. Loss Function

TFT는 Quantile Loss Function을 최소화하는 방향으로 학습을 진행합니다.

6. Performance Evaluation

(Electricity, Traffic, Retail Forecasting 실험도 있으나, TFT의 특징을 가장 잘 보여주는 Volatility 실험만 구체적으로 리뷰하였습니다.)

(1) Volatility

• Purpose : 31가지 Daily Index 데이터를 사용, 지난 252일(Intradays)의 데이터를 통해 다음주(5 Business Day)의 Volatility에 대한 예측 진행
• Duration : 2000-01-03 ~ 2019-06-28까지 데이터 사용
• Data Split : 2016년까지의 데이터를 Train, 2016-2017년 데이터를 Validation, 2018년 이후의 데이터를 Test Set으로 사용
• Regime Detection : S&P 500 Index의 Attention Vector에 Distance Metrics를 적용하여 Significant Regime Detection 이후, 해당 Regime에서의 Attention Value 값이 높음을 통해 Interpretability 검증

(2) Features

• Time Index : Dates
• Target : log of volatility(log of 5min sub-sampled realized volatility[rv5_ss])
• Observed Input : open to close(daily open-to-close returns)
• Time Varying Known Input
  - days_From_Start
  • day_of_week
  • day_of_month
  • week_of_year
  • month
• Static Covairates : Region

(3) Result

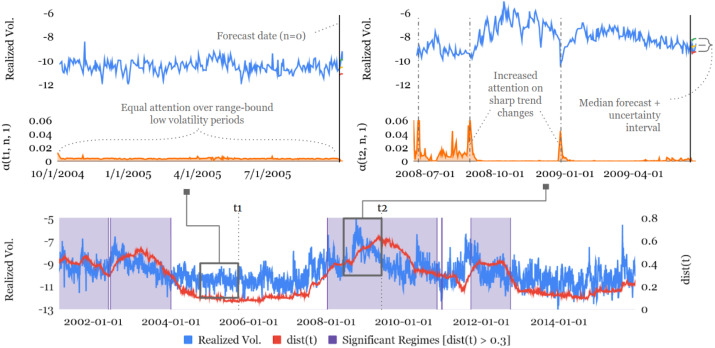
• TFT 모델의 Volatility Forecasting 과정에서 Attention Value 값을 사용하여 Regime Shift Detection 및 Interpretability를 검증하고자 하였습니다.
• 위의 그림에서 Realized Vol(파란색🔵)은 S&P 500 Index의 Volatility를, dist(빨간색🔴)은 2001년부터 2015년까지의 기간동안 TFT모델의 Attention Pattern Vector에 Distance Metrics를 적용한 결과입니다. Distance Metrics를 계산하는 수식은 아래와 같습니다.

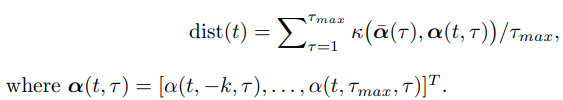
(매 시점에서의 Average Attention Pattern 정보를 담은 Attention Vector와의 거리 비교를 통해 Regime Shift Detection을 진행합니다. dist(t) rkqtdl 0.3 이상일 경우 Significant Regime으로 판단하여 보라색💜으로 표시하였습니다.)

(4) Analysis

• 2008년 경제 위기에서 dist 값이 가장 높은 것 확인할 수 있었습니다.
• Low Volatility Period(t1)에서 Attention의 변화는 크지 않으며, 전반적으로 모든 t에 대한 attention value 크기가 작은 것을 확인할 수 있습니다.
• High Volatility Period(t2)에서 Attention의 변화가 매우 크며, 2008년 financial crisis에 대해서 attention value가 높음을 확인할 수 있습니다.
• 전반적으로 Significant Regimes(보라색💜일 때 attention value의 값이 큰 것으로 보아, TFT 모델이 보아야할 부분을 잘 보고 있음을 확인할 수 있습니다.

7. Conclusion

• Time Series Forecasting에서 SOTA 알고리즘입니다.
• Time Varying Known Input을 Observed Input과 함께 학습시키면 예측 성능을 높일 수 있다는 개념을 제시하였습니다.
• Static Variable 간, Encoder Variable 간, Decoder Variable 간 Feature Importance 제공하여 모델의 Interpretability 확보할 수 있다는 것이 TFT의 큰 장점입니다.

.
.
.

References

• https://arxiv.org/pdf/1912.09363.pdf