[단단한 머신러닝] 2장 모델 평가 및 선택

환공지능·2022년 3월 22일

[단단한 머신러닝] 정리

목록 보기

2/5

2장 모델 평가 및 선택

2.1 경험 오차 및 과적합

오차율(Error Rate) : 전체 샘플 수와 잘못 분류한 샘플 수의 비율
$m$ 개의 샘플 중 $a$ 개의 샘플이 잘못 분류되었다면 오차율 $E = a/m$
정밀도(Accuracy) : '1-오차율', $1-a/m$

우리가 원하는 학습기는 새로운 샘플 데이터를 대상으로 좋은 성능을 발휘하는 학습기임. 이러한 목적을 달성하기 위해 훈련 데이터에서 모든 데이터의 잠재적인 '보편 규칙'을 찾아내야 하며, 새로운 데이터를 만났을 때 정확한 판별과 예측을 제공해야 함.

과적합(Overfitting) : 훈련 데이터에 대해 학습을 과도하게 잘해서 훈련 데이터 중의 일정한 특성을 모든 데이터에 내재된 일반 성질이라 오해하는 것
과소적합(Underfitting) : 훈련 데이터의 일반 성질을 제대로 학습하지 못했다는 것.

같은 알고리즘이라고 하더라도 파라미터에 따라 완전히 다른 모델로 불리기도 함. 어떤 학습 알고리즘을 사용해야 하며, 어떤 파라미터를 선택해야 할지의 문제를 머신러닝에서 모델 선택(Model Selection) 문제라고 부름.

이상적인 해답은 일반화 오차를 기준으로 평가한 뒤, 일반화 오차가 가장 작은 모델을 선택하는 것이지만 Train Data로 학습하는 이상 일반화 오차를 직접적으로 얻을 수 얻는 바 어떻게 모델을 평가하고 선택할 것이 이상적일까?

2.2 평가 방법

테스트라는 과정을 통해 학습기의 일반화 오차에 대해 평가를 진행하고 모델을 선택함. Test Set을 활용하여 학습기가 이전에 만나보지 못했던 새로운 샘플에서 어떻게 작동할지 예측할 수 있고, Test Set에서 나온 Testing Error를 일반화 오차의 근삿값으로 생각하게 됨.

그렇다면 $m$ 개의 샘플을 가진 데이터 세트 $D = {(x_1, y_1), (x_2, y_2), ... ,(x_m, y_m)}$ 이 있다면 우리는 어떻게 훈련하고 테스트해야할까? 해답은 데이터 세트 $D$ 를 적절히 처리하여 Train Set S와 Test Set T로 나누는 것임.

2.2.1 Hold Out

데이터세트 $D$ 를 겹치지 않는 임의의 두 집합으로 나누어 하나의 집합은 훈련 세트 $S$ 로, 나머지 집합은 테스트 세트 $T$ 로 사용하는 방법. 일반적으로 2/3 ~ 4/5 정도를 훈련 세트로 사용하고, 나머지를 테스트 세트로 분리하여 사용할 것을 권장

2.2.2 Cross Validation

교차 검증(Cross Validation)은 데이터 세트 $D$ 를 $k$ 개의 서로소 집합으로 나누는 것으로 시작함.

D = D_1 \cup D_2 \cup D_3 \cup ... \cup D_k

위와 같이 나타낼 수 있고 매 부분 집합 $D_i$ 는 되도록 데이터 분포를 반영하도록 나누어야 하며, $k-1$ 개의 부분 집합을 훈련 세트로 사용하고 나머지 하나의 부분 집합을 테스트 세트로 사용

이렇게 하면 $k$ 개의 훈련/테스트 세트가 만들어지고 $k$ 번의 훈련과 테스트를 거쳐 결과값의 평균을 얻을 수 있음. 일반적으로 $k=10$ 인 10-Fold Cross Validation이 사용됨.

2.2.3 Bootstrapping

우리는 데이터 세트 $D$ 의 모든 데이터를 활용하여 훈련시킨 모델을 평가하고 싶어함. 그러나 Hold Out이나 CV는 일부 샘플을 테스트 용도로 제외해야 하므로 모든 데이터를 훈련에 사용할 수는 없음. 이는 훈련 데이터 크기 차이로 인한 편차를 유발.

Bootstrapping은 Bootstrap Sampling에 기반을 둔 샘플 추출 기법. $m$ 개의 샘플이 있는 데이터 세트 $D$ 를 가정한다면 샘플링을 통해 데이터 세트 $D'$ 을 만든 후 매번 $D$ 에서 샘플을 꺼내 $D'$ 에 복사하여 넣음. 그리고 다시 원래의 데이터 세트 $D$ 로 돌려 보냄.

이렇게 된다면 한번 뽑혔던 샘플도 다시 뽑힐 가능성이 있으며, 이러한 과정을 $m$ 번 반복한 후 우리는 $m$ 개의 샘플이 들어 있는 데이터 세트 $D'$ 을 얻게 됨. $m$ 번의 샘플링 과정 중 샘플이 한 번도 뽑히지 않을 확률은 $(1-1/m)^m$ 이므로, 극한값을 계산하면 아래와 같은 값을 얻게 됨.

\lim_{m \to \infty} (1 - \frac{1}{m})^m = \frac{1}{e} \approx 0.368

즉, Bootstrapping을 사용하면 데이터 세트 $D$ 중 36.8%의 샘플은 $D'$ 에 들어가지 못한다고 수학적으로 계산할 수 있으며, 우리는 $D'$ 를 훈련 세트로 $D\D'$ 을 테스트 세트로 활용함. 이렇게 한다면 $m$ 개의 샘플 모두 활용하여 모델 훈련에 사용할 수 있고, 활용하지 못한 샘플들은 테스트 샘플로 활용할 수 있음.

2.4 파라미터 튜닝과 최종 모델

대부분 학습 알고리즘은 Tuning 해야 하는 Parameter가 있으며 이러한 값들을 어떻게 설정하느냐에 따라 학습 모델의 성능은 큰 차이를 보임.

모델 선택과 파라미터 조율을 위해 테스트 데이터를 활용하여 모델의 성능을 측정하기 전에 검사할 수 있는데 이 때 쓰는 데이터 집합을 Validation Set이라고 부름. Test Set을 통해 모델의 성능을 예측하나, 그 전에 Validation Set을 통해 모델의 Parameter Tuning을 진행하게 됨.

2.3 모델 성능 측정

2.3.1 재현율과 정밀도

💡 정밀도 P(Precision)와 재현율 R(Recall)은 다음과 같이 정의

P = \frac{TP}{TP + FP}

R = \frac{TP}{TP + FN}

정밀도와 재현율 사이에는 Trade Off가 존재함. 일반적으로 정밀도가 높으면 재현율은 낮고, 반대로 재현율이 높으면 정밀도는 낮은 경우가 많음.

예를 들어 수박 중 잘 익은 수박을 고른다고 할 때 모든 수박을 선택한다면 모든 '잘 익은 수박'도 선택되지만 정밀도를 매우 낮게 만들며, 만약 선택한 수박 중 잘 익은 수박의 비율을 높이고 싶어 신중하게 고르게 되면 잘 익은 수박을 고르지 못하는 비율이 올라가게 됨.

계산된 정밀도를 Y축에 재현율을 X축에 둔 그래프를 그리면 다음과 같은 정밀도-재현율 곡선을 얻을 수 있음. 간략하게 P-R이라 부르며, 해당 그래프는 P-R 곡선이라고 부름.

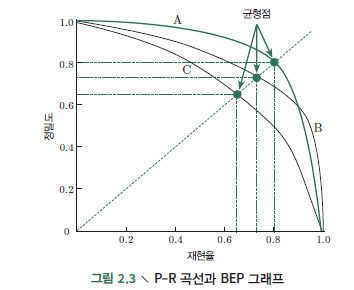
P-R 곡선은 직관적으로 샘플 전체에 대한 학습기의 정밀도, 재현율을 나타내는 바, 두 지표를 비교할 때 어던 학습기의 P-R 곡선이 다른 학습기의 P-R 곡선의 영역 내에 완전히 포함된다면, 우리는 후자가 전자보다 학습 성능이 뛰어나다고 판단할 수 있음.

그러나 두 학습기의 P-R 곡선의 교차가 발생한다면 쉽게 두 학습기의 성능을 비교할 수 없으며, P-R 곡선 아래 면적을 비교하는 것에 어려움이 있으므로 BEP(Break-Even Point)라는 성능 측도를 사용하게 됨.

BEP는 '정밀도 = 재현율'일 때의 값을 나타내는 바 위의 그림에서 A의 BEP가 0.8로 가장 좋다는 것을 알 수 있음. 하지만 BEP를 활용한 방법은 지나치게 간소화한 면이 있어서 F1 Score를 더 많이 사용하게 됨.

2.3.2 F1 Score

F1 = \frac{2~PR}{P+R} = \frac{2~TP}{Total~Sample+ TP- TN}

BEP가 너무 간소화된 경우이기 때문에 재현율과 정밀도의 조화 평균인 F1 Score를 더 많이 사용하게 됨. 위의 식에서 F1은 재현율과 정밀도의 가중치가 1인 경우, 즉 재현율과 정밀도의 중요도가 동일한 경우이나, 대부분의 경우 재현율과 정밀도의 중요도가 다를 수 있음. 이를 표현하기 위해서 가중조화 평균을 사용

F_\beta = \frac{(1+\beta^2)PR}{(\beta^2 P) + R}

\beta = 1 일 ~ 경우~F1~Score

\beta > 1 일 ~ 경우~재현율의~영향력이~더~큼

\beta < 1 일 ~ 경우~정밀도의~영향력이~더~큼

하나의 모델에 대하여 여러 번의 학습/테스트를 실행할 때 매번 하나의 혼동행렬을 구하거나 여러 데이터 세트에 대해 학습/ 테스트를 진행할 때에 혼동행렬이 다수가 됨. 이 때에 이를 종합하여 하나의 혼동 행렬로 만들어 비교하며, 그 중 한가지는 각 혼동 행렬에서 R과 P를 구하여 $(P1, R1), (P2, R2), ... , (Pn, Rn)$ 으로 기록.

이들의 평균값을 계산한 것이 매크로 정밀도, 매크로 재현율이라고 하며, 이들로 만든 F1 Score를 매크로-F1 Score라고 함. 다른 방법으로 각 혼동 행렬이 대응하는 원소에 대한 평균을 내면 TP, FP, TN, FN의 평균값을 얻을 수 있고 이를 기반으로 R과 P를 구하는 마이크로 정밀도, 마이크로 재현율, 마이크로-F1 Score도 있음.

2.3.3 ROC와 AUC

ROC 곡선은 수신자 조작 특성(Receiver Operating Characteristic)의 약자임. 신호 처리 분야에서 이 개념은 2차 세계 대전 때 레이더 신호를 분석하는 기술로 개발되어 적중 확률 대 오경보 확률을 그래프로 나타낸 것이지만 현재에는 머신러닝에서 많이 사용되고 있음. 그리는 방식은 PR 곡선과 유사하나, TPR과 FPR 값을 계산하여 x축과 y축에 그려서 완성함.

💡 TPR과 FPR은 아래와 같이 정의할 수 있음.

TPR = \frac{TP}{TP + FN}

FPR = \frac{FP}{FP + TN}

혼동 행렬과 연관지어 생각해보면 TPR은 '실제 샘플이 참값인 경우' 중에서 '모델이 제대로 참값으로 분류한 경우'의 비를 의미하며, 쉽게 말하면 '모델이 참값을 제대로 참값으로 분류해낸 비율'을 의미함. FPR은 반대로 '실제 샘플이 거짓인 경우' 중에서 '모델이 참값으로 잘못 분류한 경우의 비'를 의미하며 쉽게 말하면 '모델이 거짓을 참으로 잘못 분류해낸 비율'을 의미함.

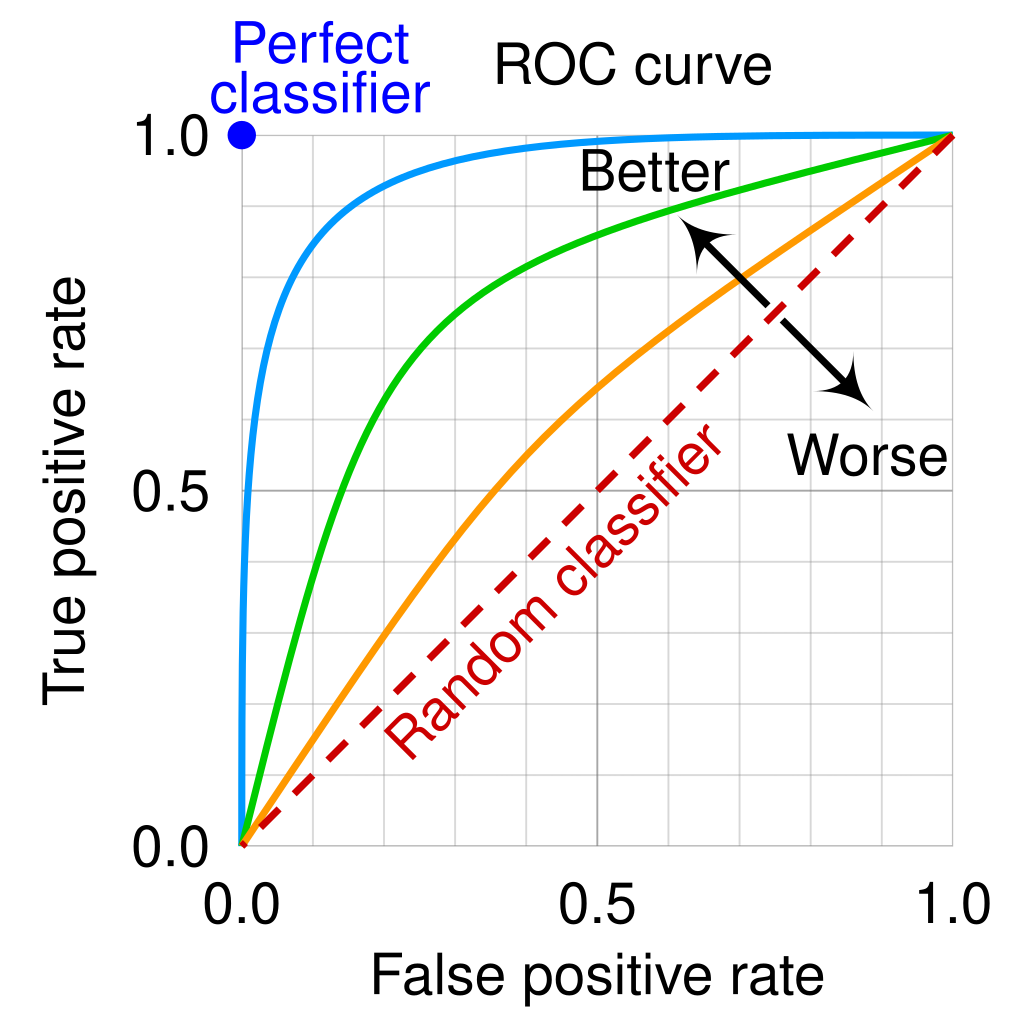
위의 그림에서 빨간색 점선은 랜덤 분류 모델을 나타낸 것으로 이것은 FPR과 TPR이 같은 경우를 의미함. TPR이 1, FPR이 0인 경우 이상적인 분류기이나 그것이 실존하기 어려운 바, ROC 곡선이 (0,1)에 가까울수록 성능이 좋다고 평가할 수 있음.

AUC(Area Under ROC Curve)는 ROC 곡선 아래 부분의 면적을 의미하는 바, 만약 ROC 곡선이 각 좌표 ${(x_1, y_1), (x_2, y_2)...(x_m, y_m)}$ 의 점들을 이어서 만들어졌다고 가정하면 다음과 같이 계산될 수 있음.

AUC = \frac{1}{2} \sum_{i=1}^{m-1} (x_{i+1} - x_i)(y_i ~+~y_{i+1})

수식은 사다리꼴 계산하는 수식과 동일함.

2.4 비교 검증

2.5 편향과 분산

우리는 테스트를 통해 학습 알고리즘의 일반화 성능을 예측하는 것 외에도 왜 이러한 성능을 얻게 되었는지도 알고 싶음. 편향-분산 분해(Bias-Variance Decomposition)은 학습 알고리즘의 일반화 성능을 해석할 수 있는 중요한 도구임.

테스트 샘플 $x$ 에 대해 $y_D$ 를 데이터 세트의 정답 데이터로 놓고, $y$ 를 $x$ 의 실제 데이터라고 한다면 $f(x; D)$ 는 훈련 세트 $D$ 에서 학습된 모델의 $x$ 상의 예측값이라고 설정할 수 있음.

📔 회귀 분석의 경우 학습 알고리즘의 기대 예측은 다음과 같이 표현 가능

\bar f(x) = E_D[f(x; D)]

📔 똑같은 샘플 수의 서로 다른 훈련 세트를 사용하여 얻어진 분산은 다음과 같음.

var(x) = E_D[(f(x; D) - \bar f(x))^2]

📔 노이즈는 다음 식과 같음

\epsilon^2 = E_D[(y_D - y)^2]

📔 기대 결과값과 실제 데이터의 차이를 편향이라고 하고 다음 식과 같이 나타낼 수 있음

bias^2(x) = (\bar f(x) - y)^2

📔 위의 식들을 사용하여 $E(f;D)$ 에 대하여 다항식 전개를 하면,

E(f;D) = bias^2(x) + var(x) + \epsilon^2

위와 같이 나타낼 수 있으며 일반 오차는 편향, 분산, 노이즈의 합으로 분해할 수 있음.

💡 편향, 분산, 노이즈의 뜻에 대해 다시 살펴보면,

편향은 학습 알고리즘의 기대 예측값이 실제 데이터에서 떨어진 정도를 측정하므로 학습 알고리즘의 적합 능력을 나타냄
분산은 크기가 같은 훈련 세트가 바뀔 때 발생하는 학습 성능의 변화를 측정하는 바, 데이터 변동에 의한 영향을 나타냄
노이즈는 해결하고자 하는 과업에서 어떤 학습 알고리즘이든지 도달할 수 있는 기대 일반화 오차의 하한선을 표현하는 바 학습 문제의 본질적인 난이도를 표현한다고 볼 수 있음.

"따라서 편향-분산 분해는 일반화 성능이 학습 알고리즘의 능력, 충분한 데이터, 그리고 학습 문제의 본질적인 난이도에 따라서 결정된다는 것을 설명함."

하지만 일반적으로 편향과 분산은 서로 상충하는 부분이 있음. 이를 편향-분산 딜레마라고 하며, 위의 그림과 같이 표현할 수 있음.

즉 훈련 정도가 크지 않은 경우 학습기의 적합 능력이 떨어져 있으므로, 훈련 데이터가 조금 변경된다고 하더라도 성능에 큰 변화가 없는 바, 이 때는 편향이 일반오차율의 원인이 될 것이며,

반대로 충분히 훈련되어 학습기의 적합 능력이 이미 매우 좋은 상태에서는 훈련 데이터에 발생한 작은 변화에도 학습기가 민감하게 반응할 것인 바 분산이 일반 오차율의 주요 원인이 될 것임.

.
.
.

Reference

단단한 머신러닝 - 머신러닝 기본 개념을 제대로 정리한 인공지능 교과서, Zhou Zhihua
https://sumniya.tistory.com/26?category=818582
https://data-manyo.tistory.com/9
https://datacookbook.kr/48

환공지능

데이터사이언티스트 대학원생

이전 포스트

[단단한 머신러닝] 1장 서론

다음 포스트