[다변수 미적분학]다변수함수 - 이변수 함수, 다변수 함수의 그래프, 등위곡선

💡오늘 배울 내용

세상의 많은 값들은 2개 이상의 변수들에 의해 결정된다고 할 수 있습니다. 일변수 함수에서 다변수 함수로 확장하여 미분, 적분을 살펴봅시다.

🔎이변수 함수

y = f(x)는 x에 따라 y가 결정되는 일변수 함수입니다. 변수가 x 하나이기 때문입니다. 좌표평면의 x축과 y축을 놓으면 일변수 함수를 그릴 수 있습니다. 다시말하면, 좌표평면상 그래프를 통해 x에 따라 어떤 y가 결정되는지 확인할 수 있습니다.

이변수 함수는 값이 x, y 두가지 변수에 의해 결정되는 함수입니다. 이변수 함수 z = f(x, y)는 좌표평면 위의 점(x, y)를 실수 z로 대응시킨다고 할 수 있습니다. 좌표평면 상에 이변수 함수 z = f(x, y)를 바로 그릴 수 없는 이유는 x, y, z 세가지 축을 이차원 상에 온전히 표현할 수 없기 때문입니다. 즉, 이변수 함수를 그릴때는 x, y, z축으로 구성되는 삼차원상의 공간이 필요합니다.

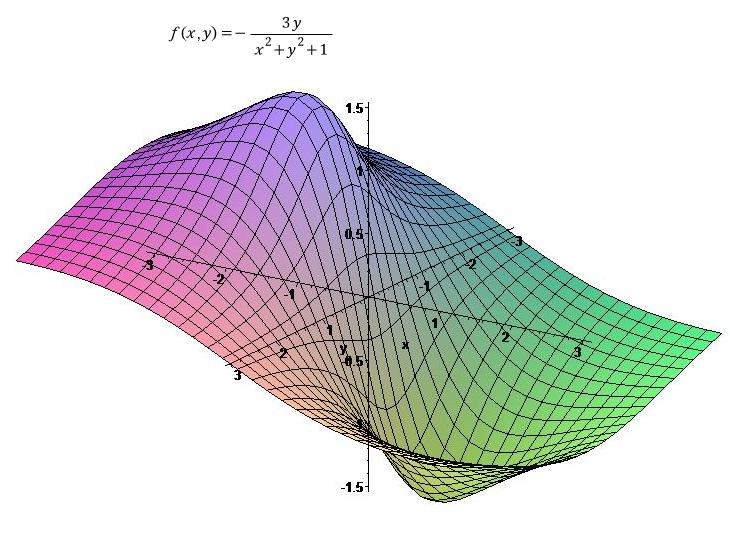
🔎등위곡선

등위곡선(Level Curves)은 이변수 함수를 그리는데 도움을 줄 수 있습니다. 또한 3개 이상의 변수로 이루어지는 함수의 성질을 파악하는데 같은 개념이 이용됩니다.

등위곡선은 이변수 함수 z = f(x, y)에 대해 f(x, y) = k(상수) 의 그래프로 정의됩니다. 이변수 함수를 예로 들어 설명하면, z값을 고정한 후 평면에 그린 그림입니다.

🔔f(x, y) = x^2+y^2

등위곡면을 활용해 이변수 함수의 그래프를 그려봅시다.

등위곡면을 그려보면 x^2 + y^2 = N을 만족시키는 xy평면의 면이 z = N에 대응됨을 보다 직관적으로 이해할 수 있습니다.

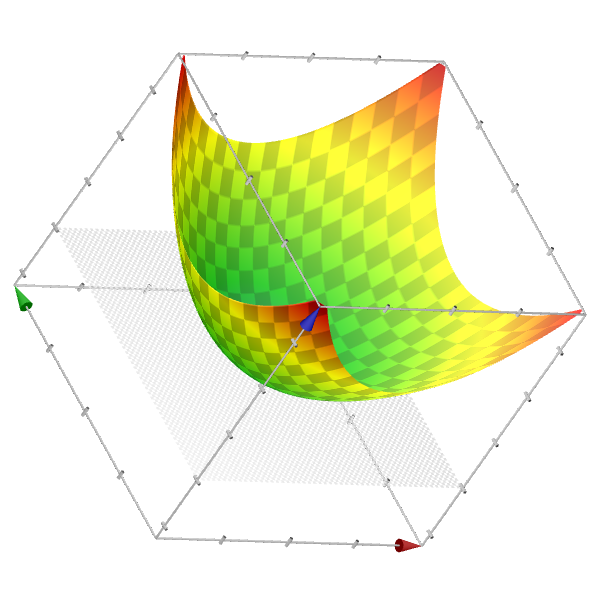
(X축 - 빨간색, Y축 - 초록색, Z축 - 파란색)

🔔f(x, y) = 9-x^2-y^2

이번에도 x, y를 축으로 하는 좌표평면에 등위곡선을 먼저 그려보고, 이를 통해 f(x, y)가 어떻게 그려지는지 대략적으로 확인해봅시다.

x, y와 z사이의 관계를 보다 직관적으로 확인할 수 있습니다.

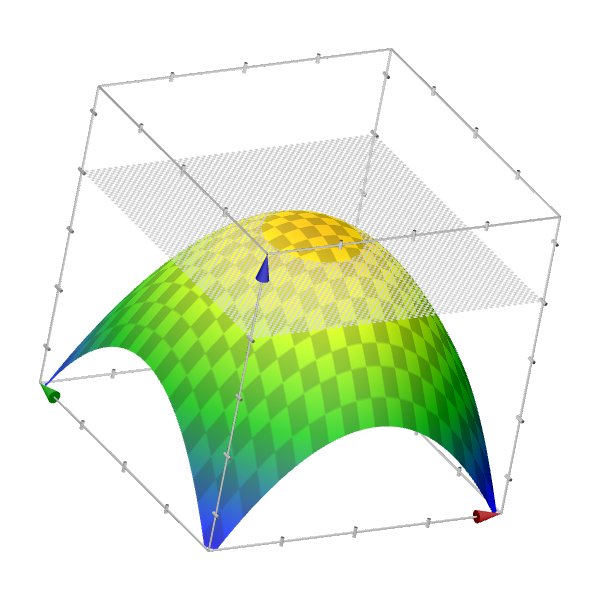
(X축 - 빨간색, Y축 - 초록색, Z축 - 파란색)

🔎등위곡면

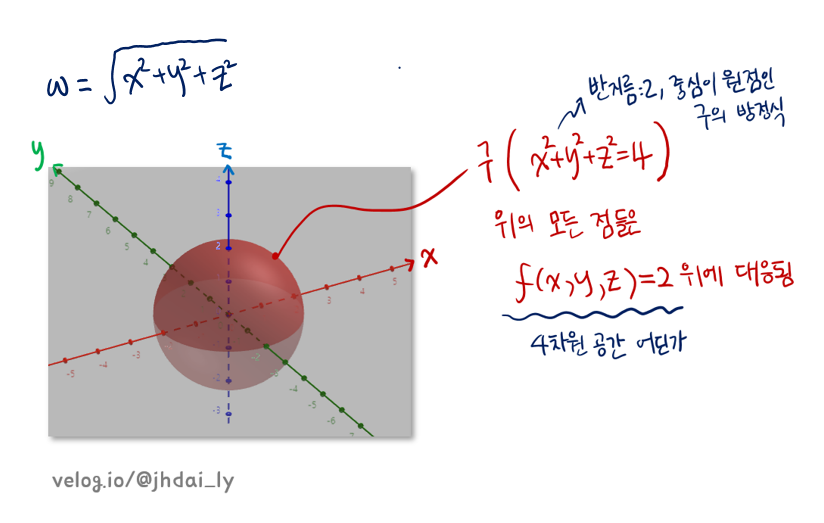
삼변수 함수는 4차원에서 정의되므로 직관적인 그래프 형태로 이해하기가 어렵습니다. 이때 등위곡면(Level Surface)을 이용하면 함수의 성질을 이해할 수 있습니다. x, y, z 세 변수로 정의되는 삼변수 함수 하나를 등위곡면을 통해 이해해봅시다.

🔔f(x, y, z) = sqrt(x^2+y^2+z^2)

등위곡면을 이용해 4차원상에 그래프를 그리려는 것이 아닙니다. 등위곡면을 생각해보면 해당 삼변수 함수의 x, y, z간의 관계를 이해할 수 있다는 것이 핵심입니다.