[다변수 미적분학]다변수 함수의 극한과 연속 - 이변수 함수의 수렴과 발산, 이변수 함수의 연속, 2-경로 테스트

💡오늘 배울 내용

다변수 함수에서 극한과 연속을 정의합니다. 일변수 함수에서 정의했던 내용과 같은 개념이지만, 3차원 공간이라는 차이점이 있습니다.

🔎이변수 함수의 연속

일변수 함수에서 정의하는 연속과 마찬가지로, 이변수 함수에서도 함수값이 잘 정의되고, 극한값이 수렴하고, 함수값과 극한값이 같을때 '연속'이라고 합니다.

그렇다면 이변수 함수의 극한값이 수렴한다는건 무슨 의미인지 이해해봅시다.

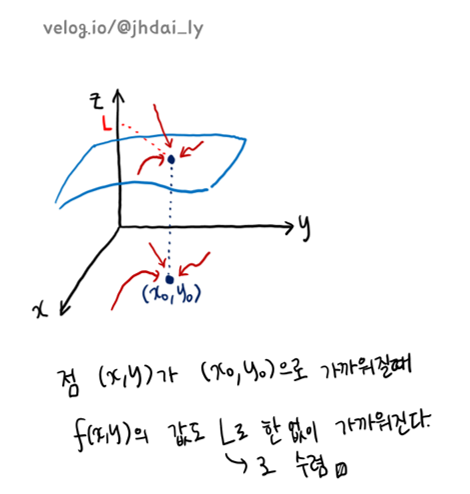
🔎수렴과 발산

일변수 함수에서의 수렴과 발산은, x가 a에 한없이 가까워질때 f(x)의 값이 L로 한없이 가까워지는지 확인하여 얻을 수 있습니다. 일변수 함수는 왼쪽과 오른쪽 방향만 존재하므로 좌극한과 우극한으로 나눌 수 있고, 이때 좌극한과 우극한이 같은 상태를 극한값이 존재한다고 정의합니다.

이변수 함수는 무수히 많은 경로로 해당 위치에 가까워질 수 있음으로 극한값이 존재하려면 하나의 반례라도 존재해선 안됩니다. 즉, 극한값이 존재하려면 이변수 함수 f(x, y)에서 점 (x, y)가 (x1, y1)로 가까워질때, 모든 경로에서 f(x, y)의 값은 L로 가까워져야 합니다.

🔎2-경로 테스트

이변수 함수의 발산을 보이는 방법으로는, 서로 다른 값으로 수렴하는 두 경로를 찾는 것입니다. 예를 들어 어떤 지점으로 향하는 두가지 방법에서, 서로 다른 값으로 수렴하면 그 함수의 그 지점에서 발산한다고 말할 수 있습니다.