
💡오늘 배울 내용
순전파 신경망 알고리즘 방식대로, 3층 신경망에서 수행되는 입력부터 출력까지의 과정을 구현해보도록 하겠습니다. 3층 신경망이란 입력층(0층)은 2개, 첫번째 은닉층(1층)은 3개, 두번째 은닉층(2층)은 2개, 출력층(3층)은 2개의 뉴런으로 구성됩니다.
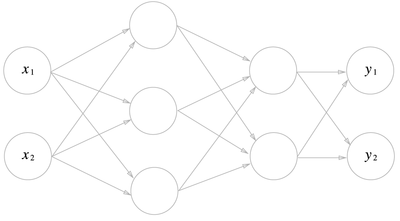
🔎가중치 표기법
신경망의 연산 방식을 다시한번 정리해보겠습니다. 입력층의 각 뉴런들에 가중치가 곱해지고, 이들의 총합이 다음 뉴런으로 전달됩니다. 활성화 함수의 처리 후 결괏값이 다시 다음 뉴런으로 전달됩니다. 일단 중요한 점은, n층의 뉴런들이 n+1층으로 전달되는 과정에서 각각의 가중치가 곱해져서 합산되어야 한다는 것입니다.
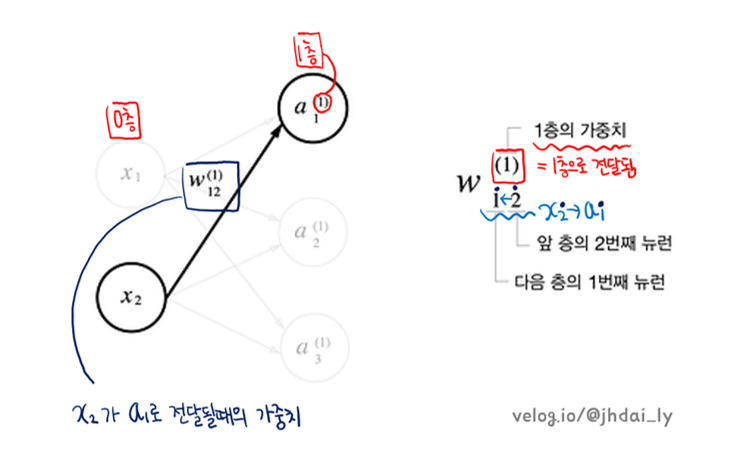
다음은 각각의 가중치를 표기하는 방법을 약속한 것입니다. 순전파 신경망을 학습하며 다른 책을 살펴보았을때 이 가중치를 표시하는 방법이 제각각 달랐지만 위의 방법을 채택하여 작성하도록 하겠습니다.
🔎신호 전달 구현
순전파 신경망에서는 왼쪽의 뉴런이 차례차례 오른쪽으로 전달됩니다. 이때 가중치가 곱해져서 합산되고 이 합산된 결과값이 은닉층에서는 활성화 함수가 적용되고, 출력층에서도 활성화 함수가 적용되지만 보통 항등 함수나 소프트맥스 함수, 시그모이드 함수가 주로 적용됩니다.
🔔입력층에서 1층으로
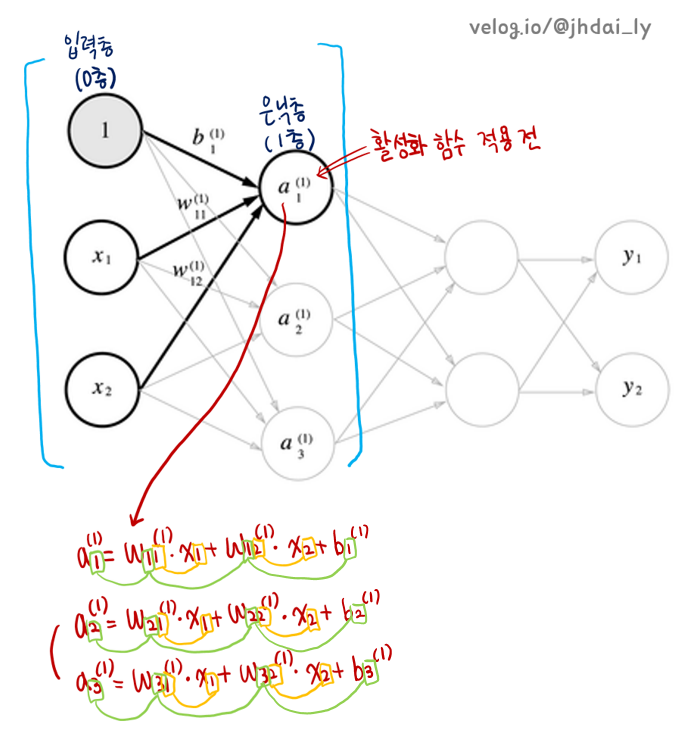
입력층(0층)에서 은닉층(1층)으로 신호가 전달될때, 입력층의 뉴런인 1, x1, x2는 a1으로도 신호를 전달하고, a2로도 신호를 전달하고, a3로도 신호를 전달합니다. 그렇다면 a1, a2, a3 각각에 어떤 신호가 전달될까요? 아래 붉은색 글씨로 적어놓은 것 처럼 각각의 뉴런들에 가중치가 곱해진 후 그들의 총합이 전달되는 것입니다.
Numpy의 스칼라곱 연산을 이용하면 은닉층의 입력되는 값들(활성화 함수 적용 전)을 쉽게 계산할 수 있습니다.
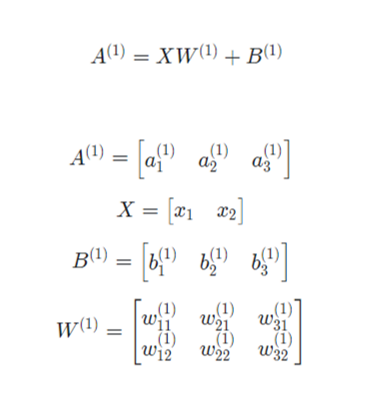
입력층의 두 뉴런의 입력값은 1.0과 0.5, 입력층과 은닉층(1층) 사이 여섯개의 가중치는 0.1, 0.3, 0.5, 0.2, 0.4, 0.6으로, b값은 각각 0.1, 0.2, 0.3으로 정하고 넘파이 코드를 작성해보겠습니다.
import numpy as np
X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])
print(W1.shape)
>> (2, 3)
print(X.shape)
>> (2, )
print(B1.shape)
>> (3, )
A1 = np.dot(X, W1) + B1A1의 계산이 Numpy dot연산으로 계산되는 과정을 머리속으로 상상해보면 알 수 있는 것 처럼 출력층의 값들이 다음 은닉층(1층)으로 전달되는 과정과 똑같습니다. 즉, 은닉층(1층)에는 a1, a2, a3에 입력값과 가중치로 만들어진 값들이 저장되는데 모두 A1 1차원 배열의 원소로 모이는 것입니다.

아까 a1, a2, a3로 모인 값들은 활성화 함수 적용 전이라고 했는데, 이제 활성화 함수를 적용하는 단계입니다. 이도 행렬 연산을 이용하면 아주 간단하게 처리할 수 있습니다. A1에 모여있는 a1, a2, a3 이 세 값들이 sigmoid 함수를 적용하는 과정을 코드로 확인해봅시다.
Z1 = sigmoid(A1)
print(A1)
>> [0.3, 0.5, 0.7]
print(Z1)
>> [0.57444252, 0.66818777, 0.75026011]🔔1층에서 2층으로
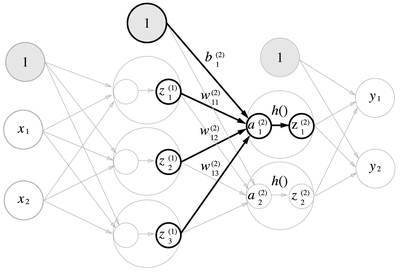
은닉층(1층)에서 은닉층(2층)으로 신호를 전달하는 과정을 살펴봅시다. 원리는 입력층에서 1층으로 전달하는 과정과 똑같습니다. 다만 이 과정에서 적용되는 가중치의 배열(2차원 배열)의 크기는 3행 2열입니다.
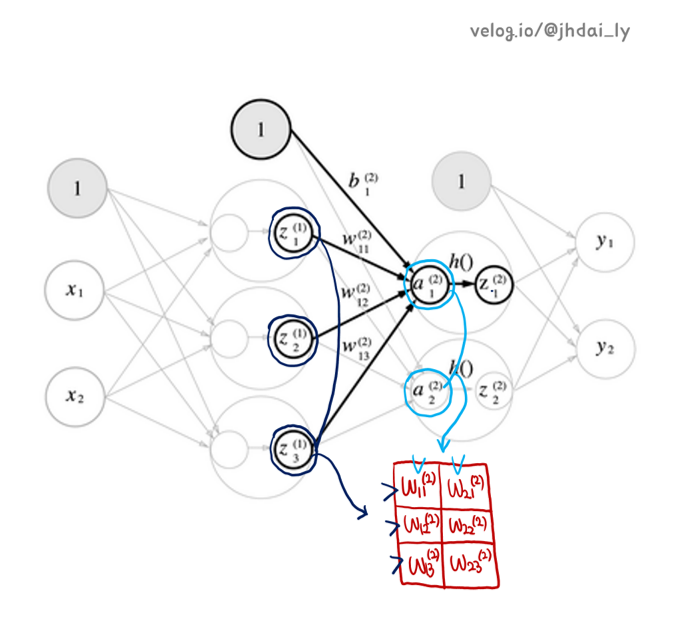
은닉층(1층)의 뉴런이 3개이고, 은닉층(2층)의 뉴런이 2개이니, 당연히 가중치가 6개인 이유는 이해 되지만, 하필 3행 2열의 2차원 배열이여야 하는 이유는 무엇일까요?
연산 후 2층 뉴런들의 값(a1, a2)을 가지고 있으려면 1행 2열짜리 배열이 필요한데요, 1행 3열짜리 배열과 n행 m열짜리 배열이 연산 하여 1행 2열이 되려면 3행 2열의 2차원 배열이 필요한 것입니다.
import numpy as np
W2 = np.array([0.1, 0.4], [0.2, 0.5], [0.3, 0.6])
B2 = np.array([0.1, 0.2])
print(Z1.shape)
>> (3, )
print(W2.shape)
>> (3, 2)
print(B2.shape)
>> (2, )
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)🔔2층에서 출력층으로
출력층의 활성화 함수는 항등함수, 시그모이드 함수, 소프트 맥스 함수 등이 쓰입니다. 문제의 성질에 맞게 정할 수 있으며 보통 회귀 문제에는 항등함수가, 이진 분류 문제에는 시그모이드 함수가, 다중 분류 문제에는 소프트맥스 함수가 사용됩니다.
여기서는 항등 함수를 적용하여 y값 두개를 추출해내는 과정을 넘파이 코드로 알아보겠습니다.

물론 2층에서 출력층으로 전달될때의 가중치 배열은 2행 2열입니다. 2층의 노드가 2개, 출력층의 노드 또한 2개이기 때문입니다.
def identify_function(x):
return x
W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])
A3 = np.dot(Z2, W3) + B3
Y = identify_function(A3)🔎구현 총 정리
init_network() 함수는 가중치와 편향을 초기화하고 이들을 딕셔너리 변수인 network에 저장합니다. 이 딕셔너리 변수 network에는 각 층에 필요한 매개변수인 가중치와 편향이 저장되어 있습니다. 그리고 forward() 함수는 입력 신호를 출력으로 변환하는 처리 과정을 구현하고 있습니다.
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def identity_function(x):
return x
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)
>> [ 0.31682708 0.69627909]