
💡오늘 배울 내용
신경망의 첫번째 시간입니다. 기존에 배운 퍼셉트론에서 신경망으로 확장해봅시다. 또한 다차원 배열의 편리한 연산 기능을 통해 신경망의 연산을 단순화하는 방법도 알아봅니다.
🔎퍼셉트론 신경망으로 해석하기
편향과 가중치가 매개변수로 작동하는 퍼셉트론(Perceptron)을 신경망으로 해석해봅시다. 신경망으로 해석하기 위해서는 입력층, 은닉층, 출력층으로 구성되는 신경망의 구조를 알아야 하고, 한 층에서 다음 층으로 넘어가는 과정과 활성화 함수의 동작에 대해서도 알아둘 필요가 있습니다.
활성화 함수는 입력신호의 총합을 출력 신호로 변환해주는 함수입니다. 출력신호로 어떻게 변환해야 원하는 문제를 해결 할 수 있을지는 나중에 자세히 배웁니다.
예를 들면 퍼셉트론은 계단 함수(Step Function)을 활성화 함수로 이용하고 있고, 출력층의 활성화 함수를 살펴보면 회귀에는 항등함수(Identity Function)를, 이진 분류에서는 시그모이드 함수(Sigmoid Function)를, 다중 분류에서는 소프트맥스 함수(Softmax Function)를 이용합니다.
바로 위에서 활성화 함수를 설명하다 보니, 퍼셉트론을 신경망 관점에서 해석할때 계단 함수(Step Function)를 활성화 함수로 이용한다는 내용을 미리 이야기했습니다.

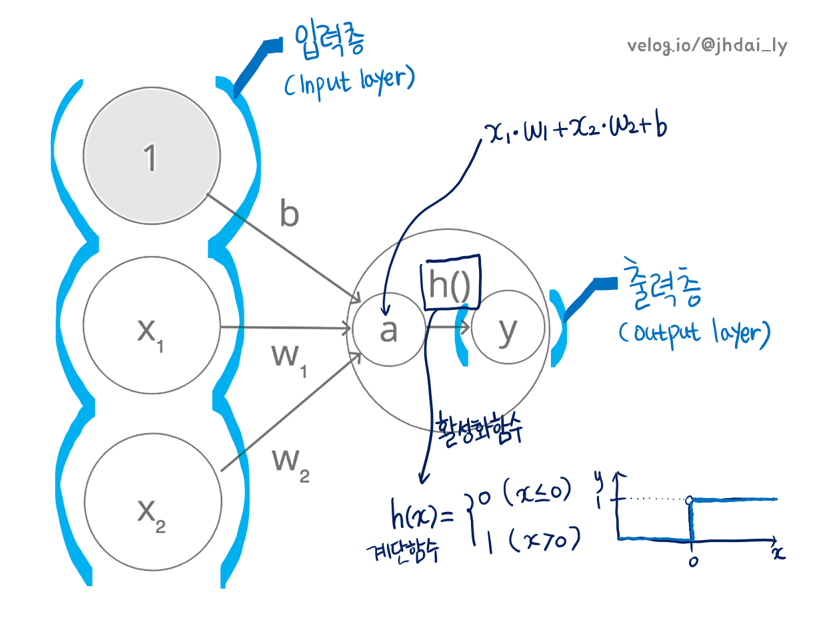
다음 그림은 퍼셉트론을 신경망으로 해석하는 과정을 모두 담았습니다. 우선 두개의 뉴런을 가진 입력층에서 해당 가중치가 곱해져 다음 뉴런으로 전달됩니다. 출력층으로 전달되기 바로 직전에 활성화 함수를 통과하는데, 여기서는 계단 함수가 사용되고 있는 것을 볼 수 있습니다. 왜냐하면 입력된 값들의 총합(여기서는 a)가 0을 넘으면 1이 출력되고 그렇지 않으면 0이 출력되는데 이러한 활성화 함수를 그래프로 나타내 보면 계단 모양을 닮았기 때문입니다.
🔎활성화 함수
앞의 주제를 설명하며 활성화 함수를 입력신호의 총합을 출력 신호로 변환해주는 함수라고 했습니다. 이번 부분에서는 활성화 함수의 종류를 알아봅시다. 퍼셉트론에서 사용되는 계단 함수도 활성화 함수입니다. 그러나 이 계단 함수를 다른 함수로 바꾸는 것이 퍼셉트론에서 신경망으로 나아가는 핵심입니다.
🔔시그모이드(Sigmoid)
impory numpy as np
def sigmoid(x):
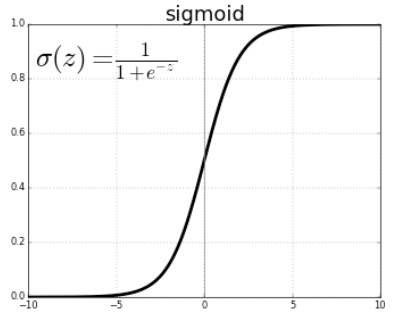
return 1 / (1+np.exp(-x))시그모이드 함수는 'S자 모양' 이라는 뜻으로 그 모양을 따 이름을 지었습니다.
층이 많을 수록 기울기가 0에 수렴하게 되는 '기울기 소실'이라는 문제가 있어 현재는 인기가 줄었지만 과거 딥러닝 자료에서 많이 찾아 볼 수 있습니다.
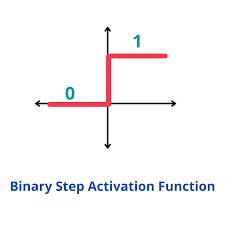
계단 함수와 비교하면 '매끄러움의 차이'가 느껴질 것입니다. 시그모이드 함수는 부드러운 곡선이며 입력에 따라 출력이 연속적으로 변화합니다.
하지만 계단 함수는 0을 경계로 출력이 바뀝니다. 즉, 계단함수는 0과 1중 하나의 값을 돌려주는 반면 시그모이드 함수는 실수를 돌려줍니다.
두 함수의 공통점도 있습니다. 둘 다 입력이 작을 때의 출력은 0에 가깝지만 입력이 커지면 출력이 1에 가까워지는 구조입니다. 즉, 두 함수 모두 활성화 함수 이므로 입력이 중요하면(=큰 값이 입력되면) 큰 값을 출력하고 입력이 중요하지 않으면(=작은 값이 입력되면) 작은 값을 출력합니다.
🔔렐루(ReLU)
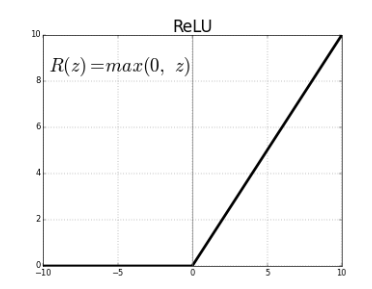
import numpy as np
def relu(x):
return np.maximum(0, x)자주 사용되는 활성화 함수인 ReLU함수입니다. 함수의 이름은 '정류된'이라는 뜻을 가진 단어 Rectified에서 왔습니다. 정류(整流)는 전기회로 쪽 용어로, 예를 들어 반파 정류회로(half-wave rectification circuit)는 +/-가 반복되는 교류에서 -흐름을 차단하는 회로입니다. 함수의 그래프를 보면 x가 0이하인 영역은 y값이 0으로 나타나는 것을 통해 함수 이름의 뜻을 이해해볼 수 있습니다.
함수의 활용, 시그모이드와 비교하여 렐루 함수의 이점 등은 추후 설명하겠습니다. 신경망의 도입 단계로써 오늘 포스팅은 활성화 함수의 종류와 모양 등만 이해해봅시다.
🔔비선형 함수
계단함수에서 시그모이드, 렐루 함수의 공통점은 모두 비선형 함수라는 것입니다. 그렇다면 선형 함수와 비교하여 비선형 함수를 활성화 함수로 사용하는 이유는 무엇일까요?
우선 선형함수는 출력이 입력의 상수배만큼 변하는 함수입니다. f(x) = ax+ b로 나타낼 수 있고, 이때 a와 b는 상수입니다. 또한 이러한 선형 함수를 활성화 함수로 이용하면 신경망의 층을 깊게 하는 의미가 없어집니다.
h(x) = cx를 활성화 함수로 사용한 3층 네트워크를 식으로 써보면 y(x) = h(h(h(x)))가 됩니다. 이 계산은 c c c * x의 계산을 수행하지만 실은 y = ax와 같은 식입니다. 즉, 은닉층이 없는 네트워크로 표현되는 것입니다. 그래서 층을 쌓아서 이득을 얻으려면 활성화 함수로 반드시 비선형 함수를 사용해야합니다.
🔎다차원 배열의 계산
신경망의 동작에 대해 연산하는 과정에서 다차원 배열의 계산(내적 연산 등)이 포함되어 있습니다. 해당 부분은 행렬의 개념 포스팅과 넘파이 dot product를 설명한 부분에서 자세히 이야기 했음으로 생략하고 넘어가도록 하겠습니다. 이 부분 개념이 궁금하신 분들은 해당 포스팅을 참고해주시기 바랍니다.

https://url.kr/zkrqmx (N차원 배열의 연산 - 사칙연산 등/내적 연산)
https://url.kr/ic8f2w (기초 행렬 - 행렬/행렬의 연산/행렬과 방정식)
