
💡오늘 배울 내용
단층퍼셉트론에서 다층퍼셉트론으로, 여기서 더 나아가면 신경망 까지 나아갈 수 있습니다. 오늘은 지난번 단층 퍼셉트론의 한계였던 XOR 게이트를 다층 퍼셉트론을 이용하여 구현해보고 신경망을 시작하기 위한 아이디어를 얻어보겠습니다.
🔎다층 퍼셉트론과 XOR
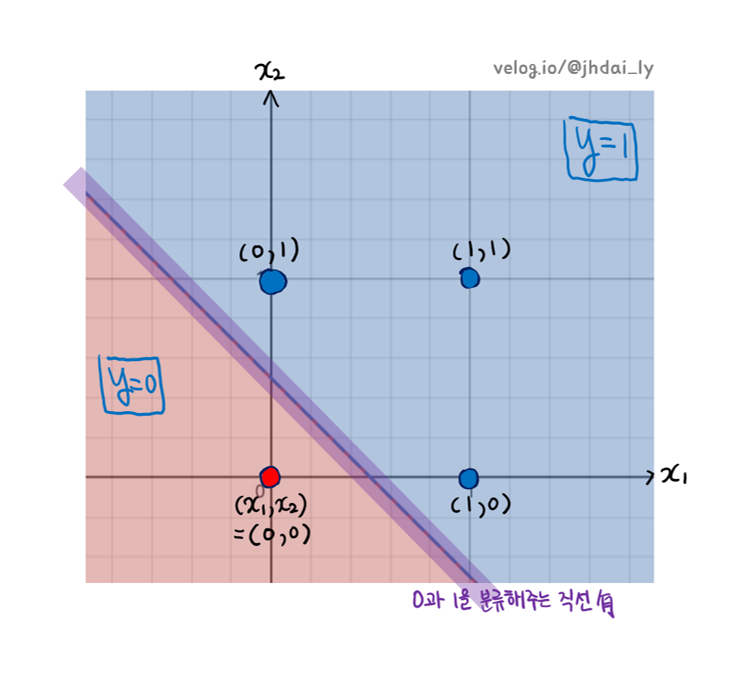
앞서서 단층 퍼셉트론이 어떠한 원리로 AND, OR, NAND 게이트 등을 구현할 수 있는지 살펴봤습니다. 결론만 이야기하자면, (단층)퍼셉트론은 매개변수에 맞는 선형 분류자를 이용하여 분류를 실행하는 것입니다.
또한, XOR 게이트를 단층 퍼셉트론이 구현할 수 없는 이유도, 마찬가지 일 것 입니다.
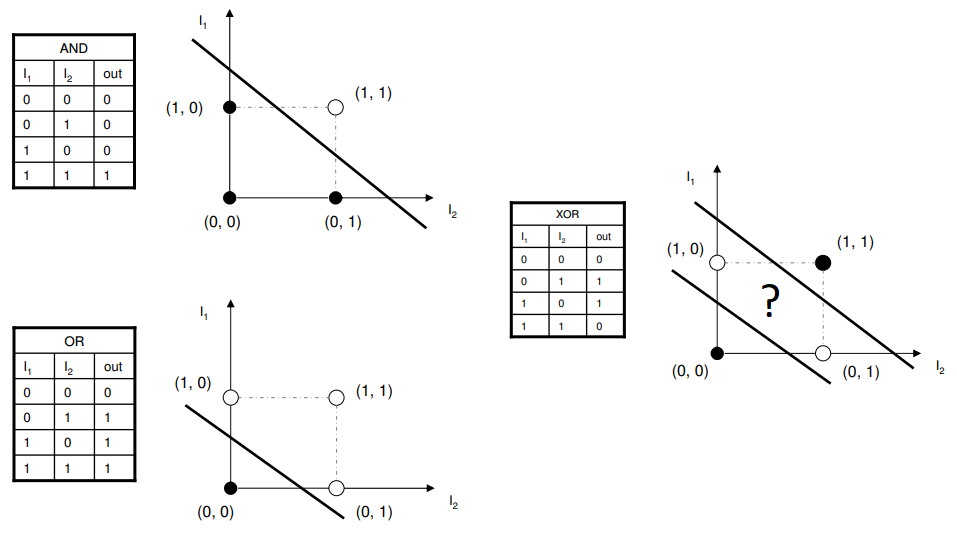
하지만 아쉬워하지 않아도 됩니다. 퍼셉트론의 층을 여러개 쌓아 다층 퍼셉트론으로 동작시킨다면 XOR 게이트를 구현할 수 있습니다. 다층 퍼셉트론은 비선형 영역의 분류 또한 할 수 있기 때문입니다.
퍼셉트론의 층을 쌓는다는 개념은 나중에 이어서 하기로 하고, 우선 OR, NAND, AND 게이트를 조합하여 XOR 게이트를 만들 수 있다는 것을 이해해봅시다. 진리표를 그리면 더 잘 이해할 수 있습니다.
def AND(x1, x2):
x = np.array([x1, x2]) #입력값을 묶어놓은 1차원 배열
w = np.array([0.5, 0.5]) #가중치를 묶어놓은 1차원 배열
b = -0.7
tmp = np.sum(w*x) + b #np.sum(w*x) == x1*w1 + x2*w2
if tmp <= 0:
return 0
else: #tmp>0
return 1
def NAND(x1, x2):
x = np.array([x1, x2]) #입력값을 묶어놓은 1차원 배열
w = np.array([-0.5, -0.5]) #가중치를 묶어놓은 1차원 배열
b = 0.7
tmp = np.sum(w*x) + b #np.sum(w*x) == x1*w1 + x2*w2
if tmp <= 0:
return 0
else: #tmp>0
return 1
def OR(x1, x2):
x = np.array([x1, x2]) #입력값을 묶어놓은 1차원 배열
w = np.array([0.5, 0.5]) #가중치를 묶어놓은 1차원 배열
b = -0.2
tmp = np.sum(w*x) + b #np.sum(w*x) == x1*w1 + x2*w2
if tmp <= 0:
return 0
else: #tmp>0
return 1
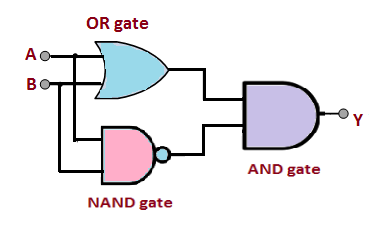
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y지난번에 구현해 본 결과물을 가져와 XOR 게이트를 구현해봅니다. 결과를 출력해보면 XOR 게이트와 똑같은 방식으로 동작하는 것을 알 수 있습니다.
XOR(0, 0) #0을 출력
XOR(1, 0) #1을 출력
XOR(0, 1) #1을 출력
XOR(1, 1) #0을 출력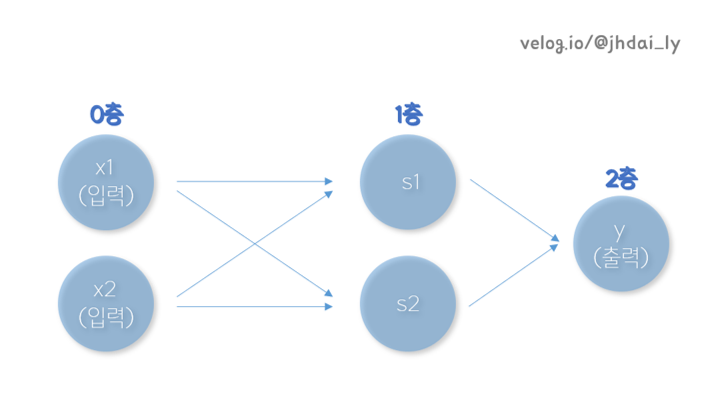
AND, OR 게이트를 퍼셉트론으로 구현했을때는 층이 하나있는 단층 퍼셉트론이었지만, XOR 게이트를 구현했을때는 한번 연산한 결과를 또 한번 더 연산해야하는 층이 2개 있는 다층 퍼셉트론입니다.
다층 퍼셉트론으로 비선형 영역의 분류도 할 수 있는 것이 입증되었습니다. 다층 퍼셉트론으로 XOR 게이트를 구현할 수 있기 때문입니다. 그 원리는 AND, NAND, OR 게이트를 조합하여 XOR 게이트로 탄생시킨 것이지만 말입니다.
이처럼 단층 퍼셉트론으로 표현하지 못한 것을 층을 하나 더 늘려 구현할 수 있습니다. 이처럼 퍼셉트론은 층을 쌓아 더 다양한 것을 표현할 수 있답니다.
🔎NAND에서 컴퓨터까지
NAND GATE의 조합만으로 컴퓨터를 만들 수 있다!
『The Elements of Computing System:
Building a Modern Computer from First Principles』(The MIT Press, 2005)
컴퓨터의 동작은 다양한 요소들의 연산 결과가 모여지는 것에 불과합니다. 즉 덧셈을 처리하는 가산기, 인코더, 패리티 검사 회로와 같은 작은 모듈들을 구현하는 것이 가능하다면 이러한 모듈이 매우 많이 모여 컴퓨터가 되는 것입니다.
이론상 2층 퍼셉트론이면 컴퓨터를 만들 수 있다고 밝혀져 있습니다. 정확히는 비선형인 시그모이드 함수를 활성화 함수로 이용하여 임의의 함수를 표현할 수 있습니다. NAND 등의 저수준 소자에서 시작하여 AND와 OR 게이트, 반가산기와 전가산기, 그 다음에는 산술 연산 장치(ALU)와 CPU로 이어지는 흐름입니다.
🔎퍼셉트론에서 신경망으로
퍼셉트론으로 컴퓨터까지 표현할 수 있다는 점은 매우 이상적으로 들리지만, 한가지 나쁜 소식은 가중치를 설정하는 작업이 여전히 사람의 몫이라는 점입니다.
다행이도 퍼셉트론에서 신경망으로 한차원 넘어오면 이러한 나쁜소식이 해결됩니다. 즉, 신경망은 가중치 매개변수의 적절한 값을 데이터로부터 자동으로 학습하는 능력이 핵심입니다.
매개변수를 자동으로 학습하는 방법은 조금 더 나중에 이야기 하도록 하고 우선 간단한 신경망의 동작 원리와 개념에 대해서 배워봅시다.
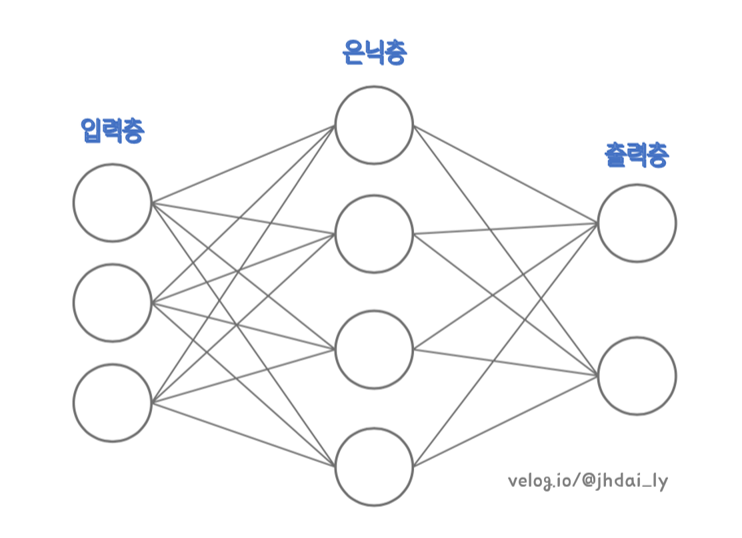
얕은 신경망 하나를 가져와 신경망의 구조를 이해해볼 수 있습니다. 가장 왼쪽 층을 입력층, 가장 오른쪽 층을 출력층, 중간 부분을 은닉층이라고 할 수 있습니다. 은닉 계층의 결과 값은 마지막 계층과는 다르게 명백하기 드러나지 않기 때문에 그러한 이름이 붙었습니다.
