[머신러닝(ML)]다중선형회귀(Multiple Linear Regression)-원 핫 인코딩, 다중 공선성, 회귀 모델 평가지수(MAE, MSE, RMSE, R square), 사이킷런(Sklearn) 실습

💡오늘 배울 내용

다중 선형 회귀 모델을 만들고 평가해봅시다. 범주형 데이터를 전처리 하고, 다중 공선성을 해소하기 위한 사이킷런(sklearn) 라이브러리의 클래스를 살펴봅시다.

🔎다중 선형 회귀

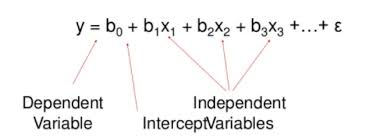
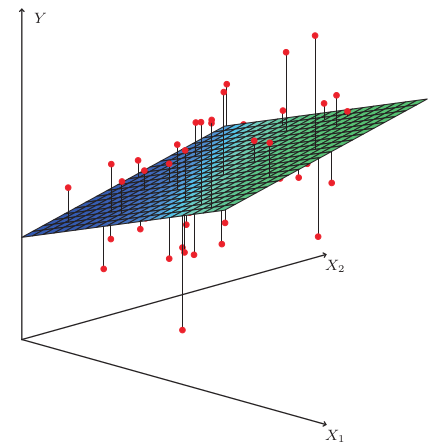
이전에 공부했던 단순 선형 회귀는 모델의 결과값 예측을 위한 독립 변수가 1개인 경우입니다. 예를 들면 공부 시간을 통해 시험 점수를 예측하는 모델을 만들려면 공부 시간(X;독립 변수)과 시험 점수(y;결과 값) 간의 관계를 유추해야합니다.

다중 선형 회귀는 하나의 모델 안에 독립 변수가 여러개일 수 있습니다. 여러 독립변수를 함께 고려한 종속 변수를 예측하기 때문에 단순 선형회귀보다는 더 좋은 성능을 기대할 수 있습니다. 예를 들면 시험 점수를 예측하는 모델을 만들고자 할때, 결석 횟수와 공부 장소, IQ와 수업 집중도 등을 함께 고려하는 경우 종속 변수에 영향을 미치는 독립변수가 여러개 일 것입니다.

🔔다중 공선성

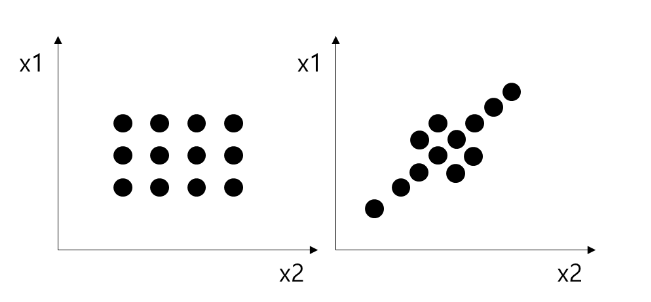
통계적으로 회귀 분석을 진행할때, 다중 공선성 문제를 고려할 필요가 있습니다. 다중 공선성 문제란 회귀분석에서 독립변수들 간에 강한 상관관계가 나타나는 문제를 말합니다. 상단의 우측 사진 처럼 x1와 x2간의 양의 상관관계가 존재하는 경우 다중 공선성이 있다고 할 수 있습니다.

독립 변수가 많이 투입되면, 결정 계수는 높아지는 경향성이 있지만 회귀 계수는 신뢰하지 못하게 될 수 있습니다. 공차 한계(Tolerance)와 VIF(Variance Inflation Factor)를 통해 검정 할 수 있으며 다중공선성이 높은 독립변수가 있다면 그 변수를 삭제하는 것을 고려해야 합니다.

구체적으로 이야기해보면, 선형 모델을 만든다는 것은 독립 변수와 결과값 간의 관계를 설명하는 선형 모델의 가중치(=회귀 계수)를 찾는 것입니다. 여기서의 회귀 계수가 의미하는 것은 독립 변수 x의 한 단위가 바뀔때 결과 값 y가 변하는 정도를 말하는데, 회귀 계수끼리 상관성이 높다면 결과값 y가 변화하는 것이 x1 혹은 x2의 독립적인 영향 만을 의미하는지 확신할 수 없게 됩니다.

🔔범주형 데이터 전처리(One-hot Encoding)

분석을 위해 사용하는 모델은 수치형 데이터만 다룰 수 있습니다. 즉, 문자열로 된 데이터를 전처리하는 과정이 필요한데요. 주요 기법인 라벨 인코딩(Label Encoding)과 원 핫 인코딩(One-hot Encoding)중 원 핫 인코딩 기법을 알아보겠습니다.

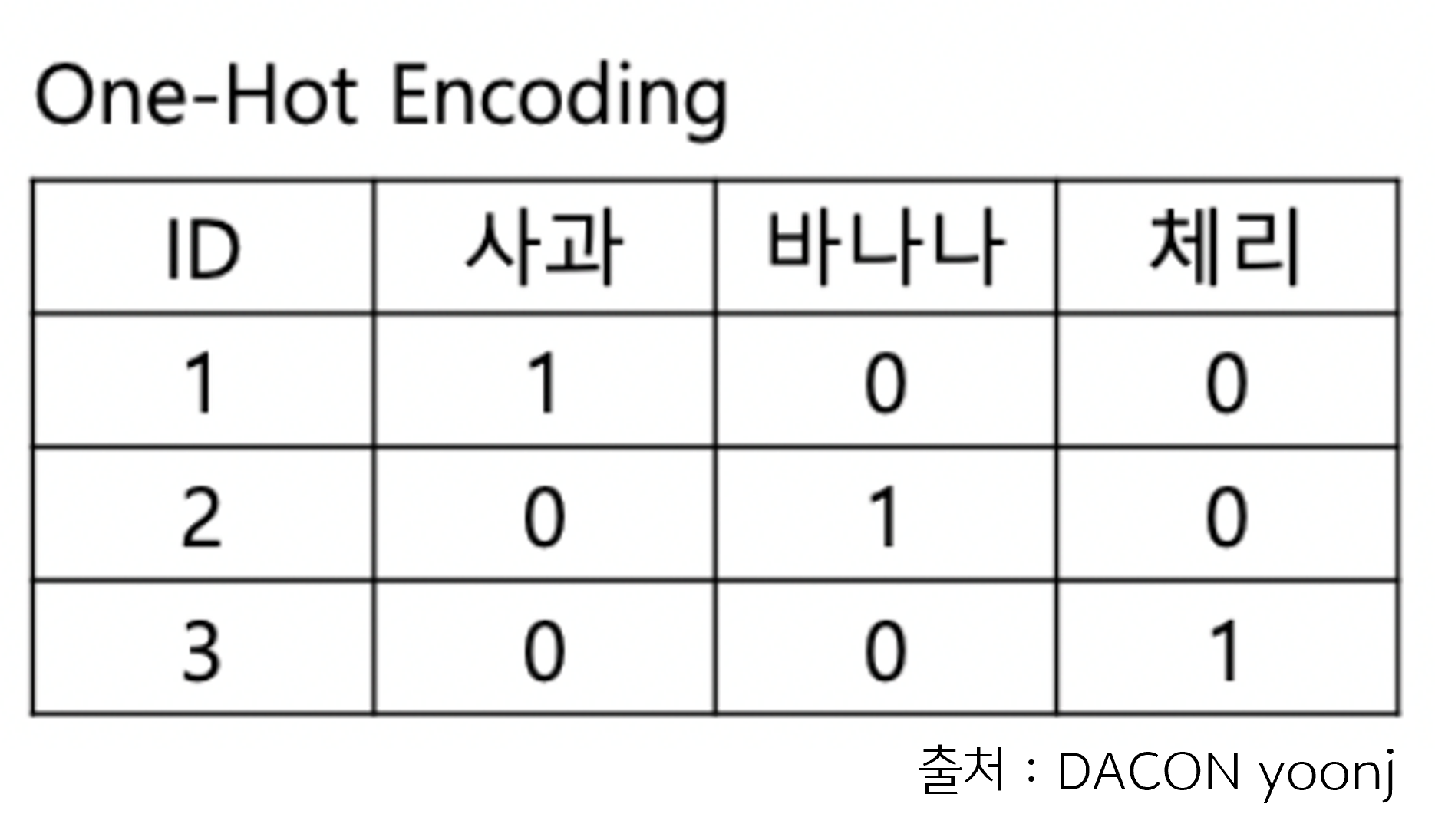
원 핫 인코딩은 범주형 데이터의 각 카테코리를 0과 1로 된 벡터로 나타내는 방법입니다. 카테고리의 수 만큼 벡터가 생성되어 숫자의 크고 작은 특성(중요도)를 없앨 수 있습니다. 이 부분은 라벨 인코딩(Label Encoding)과 차이가 나는 부분입니다.

우리는 사이킷런의 하위 패키지 sklearn.processing의 OneHotEncoder을 통해 해당 실습을 진행할 것입니다.

🔎모델 평가지수

회귀 계수가 다 구해진 완성된 선형 모델을 평가하기 위해 몇가지 지표가 사용됩니다. 모델 성능 평가란 실제값과 모델에 의해 예측된 값을 비교하여 두 값의 차이를 구하는 것입니다. 현실적으로 예측값과 실제 값이 정확히 같을 수는 없기 때문에 오차를 구하고, 어느정도까지 오차를 허용할지 결정하는 과정을 거쳐야합니다.

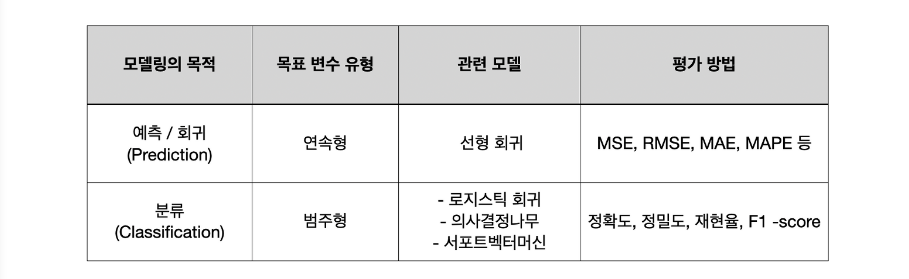
모델평가를 통해 과적합을 방지하고 최적의 모델을 찾고자 노력합니다. 과적합이란 훈련 데이터에 만 과하게 훈련된 경우로, Validation 데이터를 사용하여 평가했을때 성능이 확연하게 떨어진다면 과적합된 상태로 볼 수 있습니다. Output Label이 존재하는 지도학습에서만 사용할 수 있으며 모델링의 목적에 따라 서로 다른 평가지표가 이용됩니다.

🔔MAE

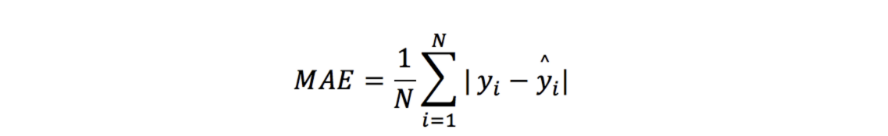
MAE(Mean Absolute Error : 평균 절대 오차)
: 실제 값과 예측값의 차이를 절댓값으로 변환해 평균낸 것.

🔔MSE

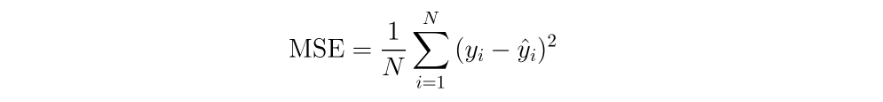
MSE(Mean Squared Error : 평균 제곱 오차)
: 실제값과 예측값의 차이를 제곱해 평균낸 것.

🔔RMSE

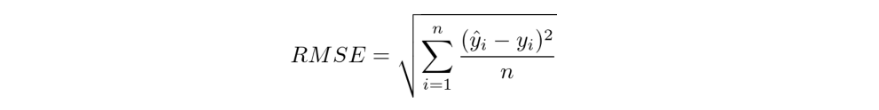
RMSE(Root Mean Squared Error : 평균 제곱근 오차)
: MSE가 제곱을 통해 구해지는 과정에서 값이 커지므로 이를 제곱근으로 보정한 것.

🔔R Square

R square
: 결정계수 (데이터의 분산을 기반으로 한 평가 지표)
: 1에 가까울수록 좋은 모델

🔎실습(Sklearn)

사이킷런 라이브러리를 통해 공부 시간, 결석 횟수, 공부 장소를 독립 변수로 하고 시험 점수를 결과값으로 하는 모델을 훈련하고 평가해봅시다.

🔔실습 자료

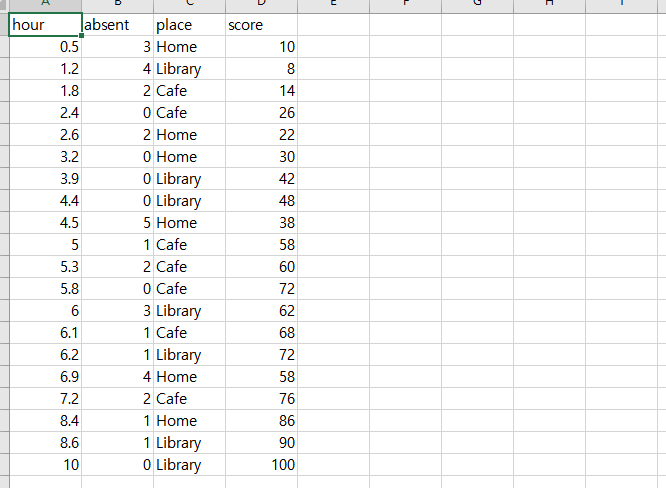
공부 시간, 결석 횟수, 공부 장소와 점수가 담겨있는 CSV 파일을 판다스 라이브러리로 불러 사용합니다. 공부 장소(place)는 범주형 자료이므로 One-hot Encoding을 통해 전처리를 진행합니다.

🔔모델 훈련 및 평가

import pandas as pd
dataset = pd.read_csv('MultipleLinearRegressionData.csv')
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
>> X

실습 자료에서 확인했던 것 처럼, 판다스 read_csv를 통해 자료를 가져옵니다. X에는 독립변수들의 데이터를, y는 결과값을 넣어 줍니다.

# 다음은 사이킷런 라이브러리의 하위 패키지로 따로 임포트 해주어야 한다.
# from 패키지이름 import 명령어1, 명령어2, 명령어3

from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder

# 다중 공선성 고려 - drop='first'
ct = ColumnTransformer(transformers=[('encoder', OneHotEncoder(drop='first'), [2])], remainder='passthrough')
X = ct.fit_transform(X)
X

# 1 0 : Home
# 0 1 : Library
# 0 0 : Cafe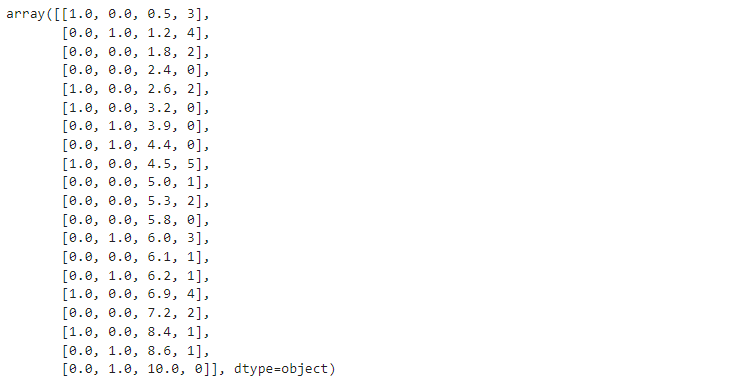

사이킷런의 하위 패키지에 들어있는 ColumnTransformer과 OneHotEncoder를 사용하여 범주형 자료를 전처리(원-핫 인코딩) 해줍니다. OneHotEncoder의 drop 옵션을 사용해 다중 공선성을 고려해줍니다. Dummy Column이 n개면, n-1개만 사용함으로써 다중 공선성 문제를 해결하는 과정입니다.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

훈련 세트와 테스트 세트를 분리해주는 과정입니다. 사이킷런 sklearn.model_selection 패키지의 train_test_split을 이용합니다.

from sklearn.linear_model import LinearRegression
reg = LinearRegression()
reg.fit(X_train, y_train)
>> LinearRegression()

사이킷런 LinearRegression 클래스, LinearRegression(), fit() 메서드를 통해 다중 선형 회귀 모델을 훈련합니다.

y_pred = reg.predict(X_test)
y_pred
>> array([ 92.15457859,  10.23753043, 108.36245302,  38.14675204])

y_test
>> array([ 90,   8, 100,  38], dtype=int64)

만들어진 선형 모델(reg)에 테스트 세트를 넣어 예측 결과를 출력해봅니다. y_test(결과값)과 비교해보면 어느정도 비슷한 것을 확인할 수 있습니다.

reg.coef_ #독립 변수에 대한 회귀 계수(기울기) 정보
>> array([-5.82712824, -1.04450647, 10.40419528, -1.64200104])

reg.intercept_
>> 5.365006706544733

coef_와 intercept_를 통해 모델의 기울기와 절편을 확인할 수 있습니다.

reg.score(X_train, y_train)
>> 0.9623352565265528

reg.score(X_test, y_test)
>> 0.9859956178877445

모델의 정확도를 확인하는 모델 평가입니다. 훈련 세트를 통해 확인한 정확도와 테스트 세트를 통해 확인한 정확도를 둘 다 확인할 수 있습니다.

from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, y_pred) #실제값, 예측값 # MAE
>> 3.225328518828811

from sklearn.metrics import mean_squared_error
mean_squared_error(y_test, y_pred) #실제값, 예측값 # MSE
>> 19.90022698151514

from sklearn.metrics import mean_squared_error
mean_squared_error(y_test, y_pred, squared=False) #실제값, 예측값 # RMSE
>> 4.460967045553591

from sklearn.metrics import r2_score
r2_score(y_test, y_pred) # R2
>> 0.9859956178877445

회귀 모델을 평가하는 지표입니다. MAE, MSE, RMSE, R2등 다양한 지표들을 사이킷런 라이브러리에서 제공하는 sklearn.metrics 패키지를 통해 확인해 볼 수 있습니다.