Prefix

이전 post에서 Turing Machine을 언급했습니다. 부차적 설명을 적습니다.

Concept

Turing Machine은 Automata의 한 종류로, 기록을 할 수 있는 무한의 tape(memory), tape에 기록을 할 수 있는 기호, 기호를 읽거나 쓸 수 있는 head로 구성됩니다.

여기서 Automata란 이미 정한 rule을 따라 task를 수행하는 것을 총칭하는 것으로, FSM, PDA, LBA 혹은 cellular automata나 quantum automata등이 있습니다. 우리가 다룰 Turing Machine은 아래 그림처럼 생겼습니다.

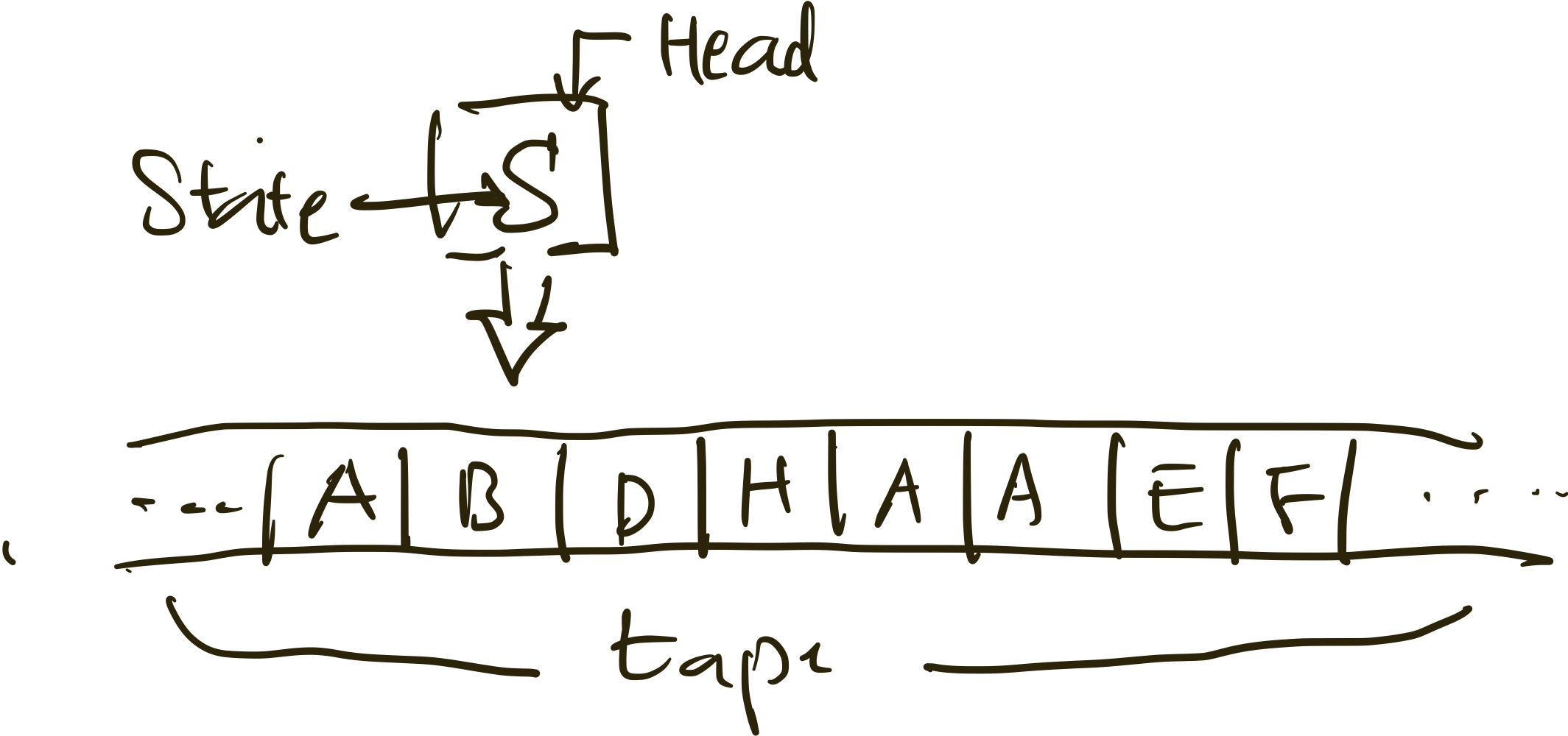
Head: State를 가지고 있고, 현재 위치한 cell을 읽고 쓰거나 좌우 이동이 가능한 장치
Tape: 기호 하나를 읽고 쓸 수 있는 Cell이 무한히 연결된 기억 장치
기호 집합: Tape에 읽고 쓸 수 있는 기호들의 집합
상태 집합: Turing Machine이 가질 수 있는 state들의 집합
명령 테이블: 현재 상태와 기호에 따라 할 일을 지정하는 명령 목록

Turing Machine의 작동을 그림으로 표현하겠습니다.

전부 0으로 초기화된 tape memory 에 1111=15를 기록하는 원시적인 Turing Machine입니다.(2개 state를 사용하여 1로만 채웠으니 2-State Busy Beaver 이네요)

이러한 Turing Machine을 통해, $input+1=output$ 을 하는 Algorithm을 만들 수도 있고, 곱하기 2를 해주는 Turing Machine을 만들 수도 있습니다. 그리고 이러한 Algorithm들은, 100011010...처럼 0과 1의 나열로 만들 수 있습니다. $S_0 -> A$, $S_1 -> B$로 쉽게 바꾸어 쓴다면 No.2의 규칙은 $_A1_L$ 로 짧게 쓸 수 있고, 이건 다시 0101110(A->0, 1->10, L->1110)의 binary로 고쳐쓸 수 있습니다.

숫자에 1을 더하는 Turing Machine은 101011010111101010 = 177642이고, 곱하기 2를 수행하는 Turing Machine은 십진법으로 1456581339라고 합니다. 그럼 십진법으로 0인, 가장 작은 Turing Machine은 무엇일까요? 얘는 테이프를 바꾸지 않고 그냥 오른쪽으로 쭉 가는, 아무 기능도 하지 않는 Turing Machine입니다. 버그가 있는 Turing Machine도 있다고 합니다.

그런데 위의 테이블에서는 $H$라는 정지하는 부분이 있었습니다. 그리고 가장 작은 Turing Machine 0짜리는 그냥 오른쪽으로 쭉 가서 $H$가 없고 정지하지 않습니다.

어떤 Turing Machine이 정지 할 지 안 할 지 알 수 있을까요?

Halting Problem

어떤 프로그램의 Turing Machine을 Head가 읽고, 그게 끝날 지 안 끝날 지 알 수 있는 Turing Machine $H$가 있다고 합시다. 끝나지 않는다고 계산하면 Tape에 1을, 끝난다고 계산하면 Tape에 0을 기록합니다.

$H$ Turing Machine의 output을 input으로 받는 $N$ Turing Machine도 있다고 칩시다.
$H$ Turing Machine 이 끝난다는걸 안 $N$ Turing Machine은 끝납니다.
$H$ Turing Machine 이 안 끝난다는걸 안 $N$ Turing Machine은 안 끝납니다.
즉 끝난다/끝나지 않는다의 결과를 반대로 출력합니다.

$H$와 $N$을 이어붙인 머신을 $HN$ Turing Machine이라고 합시다. 그리고, $HN$ Turing Machine의 십진법 코드 숫자를 다시 $HN$ Turing Machine이 받는다고 합시다. 이것의 목적은 $HN$ Turing Machine이 멈추는지 안 멈추는지를 $H$ Turing Machine이 말해줄 수 있는가입니다.
그러면,

$HN$ Turing Machine 멈춤: $H$가 멈춘다 -> $N$이 멈추지 않는다 -> $HN$은 멈추지 못한다 (모순)
$HN$ Turing Machine 안 멈춤: $H$가 안 멈춘다는 결과 출력 -> $N$이 멈춤 (모순)

이게 Halting Problem의 결론입니다. 어떠한 계산 기계도 Turing Machine이 풀 지 못하는 문제는 풀 수 없습니다. 즉 Turing Machine을 통해 Computable의 한계를 정의할 수 있습니다.

1강에서, Shannon에 따르면 정보의 최소 단위는 비트였습니다. 모든 정보는 0,1로 표현 가능하고, Turing Machine은 0과 1을 바꿀 수 있습니다. AND, OR, NOT 등을 이용하여 사칙연산도 가능하고, Church Turing thesis에 따르면 사칙연산이 가능하다는 것은 모든 연산이 가능하다는 것과 동일하다고 합니다.