Prefix

전 포스트에서는 양자 컴퓨터를 만들어야 할 하드웨어적 이유에 대해 얘기해보았습니다. 이번 포스트에서는 소프트웨어적(?) 이유를 하나 들어볼까 합니다.

Computability & Algorithms

Computation의 목표는 Information을 Transform 시키는거로 정의됩니다.

Information을 transform 시킨다, 어떤 함수에 input을 넣고 output을 내뱉는, 그런 algorithm에 대해 생각해봅시다.

Algorithm이란 DTM(Deterministic Turing Machine)입니다. DTM은 finite number of steps가 있고, thinking effort 를 필요로 하지 않습니다. 좀 더 쉽게 쓰면, DTM이란 유한한 과정으로 rule을 수행하는 가상의 기계입니다. 어떤 함수가 Computable하다는 것은, 어떤 DTM이 그 함수를 Compute 할 수 있다는 뜻입니다.

Algorithm(DTM) = Finite tuple of finite set and set's element. This computes function

과연 Algorithm은 몇 개가 있을까요? DTM(Algorithm)은 성질대로 finite set of {0,1}로 나타낼 수 있습니다. 그리고 이러한 string은 2개의 자연수로 바꿀 수 있습니다. 예를 들어봅시다 🙂

어떠한 DTM이 0000010010100001010100... 라고 합시다.
앞줄의 0의 갯수(5개)를 하나의 자연수로, 그걸 제외한 나머지 수를 또 다른 자연수로 변환할 수 있습니다. 즉 어떠한 DTM을 2개의 수, $\mathbb{N^2}$으로 나타낼 수 있습니다.
즉 DTM은 countable infinite 개 있습니다.

다시 말하면, Algorithm은 정의부터 finite number of steps or instructions을 가져야 해서 uncountably infinite하지 않습니다. 그럼 function은 어떨까요? Real-number에서 real-number로 mapping하는 functions의 경우 real-number가 uncountably infinite 하기에 function의 cardinality는 continuum입니다.

Algorithm이 information의 transform을 compute하는 거였는데, function(uncountably infinite)과 algorithm(countably infinite)의 범위가 같지 않네요 🥺

Alan Turing은 Halting Problem이 계산 불가 함수라는걸 증명했습니다. 해당 증명에는 DTM이 DTM을 analyze 할 수 없다는 내용이 나오는데, 만약 Church Turing Thesis가 맞다면 우리는 DTM이므로 모든 Computer를 Analyze할 수 없습니다. 바꿔 말하면, 세상에는 우리가 이해할 수 없는, 결정론적으로 예측할 수 없는 컴퓨터가 있다는 뜻입니다. Turing Machine에 대한 내용은 다음 포스트에서 조금 더 다루겠습니다.

그렇지만 위에서 말한 Non-computable function은 이제 철학자의 일로 미룹시다. 우리는 Computing에 대한 공부를 하고 있으니 Computable function만 신경쓰도록 하죠.

그렇지만 모든 Computable 문제가 다 같은 건 아닙니다. 모든 edge를 한 번 씩 가는 Euler path문제는 쉽습니다. 그러나 모든 vertex를 한 번 씩 가는(외판원 문제) Hamiltonian path 문제는 해의 Existence도 모릅니다. 좋은 Algorithm이 있다는 뜻은, 나쁜 Algorithm도 있다는 뜻입니다.

n개의 숫자로 이루어진 두 자연수 a, b가 있습니다.
덧셈은 2n개의 element를 addition하는 문제이고, 복잡도는 2n으로 $O(n)$입니다.
곱셉은 n^2로 $O(n^2)$인 tractable polynomial 문제입니다.

Untractable이지만 polynomial일 수 있고, 아닐수도 있습니다. 위에서 말한 Halting Problem이나 Hamiltonian Path 문제는 아예 polynomial 문제가 아닙니다.

P=NP?

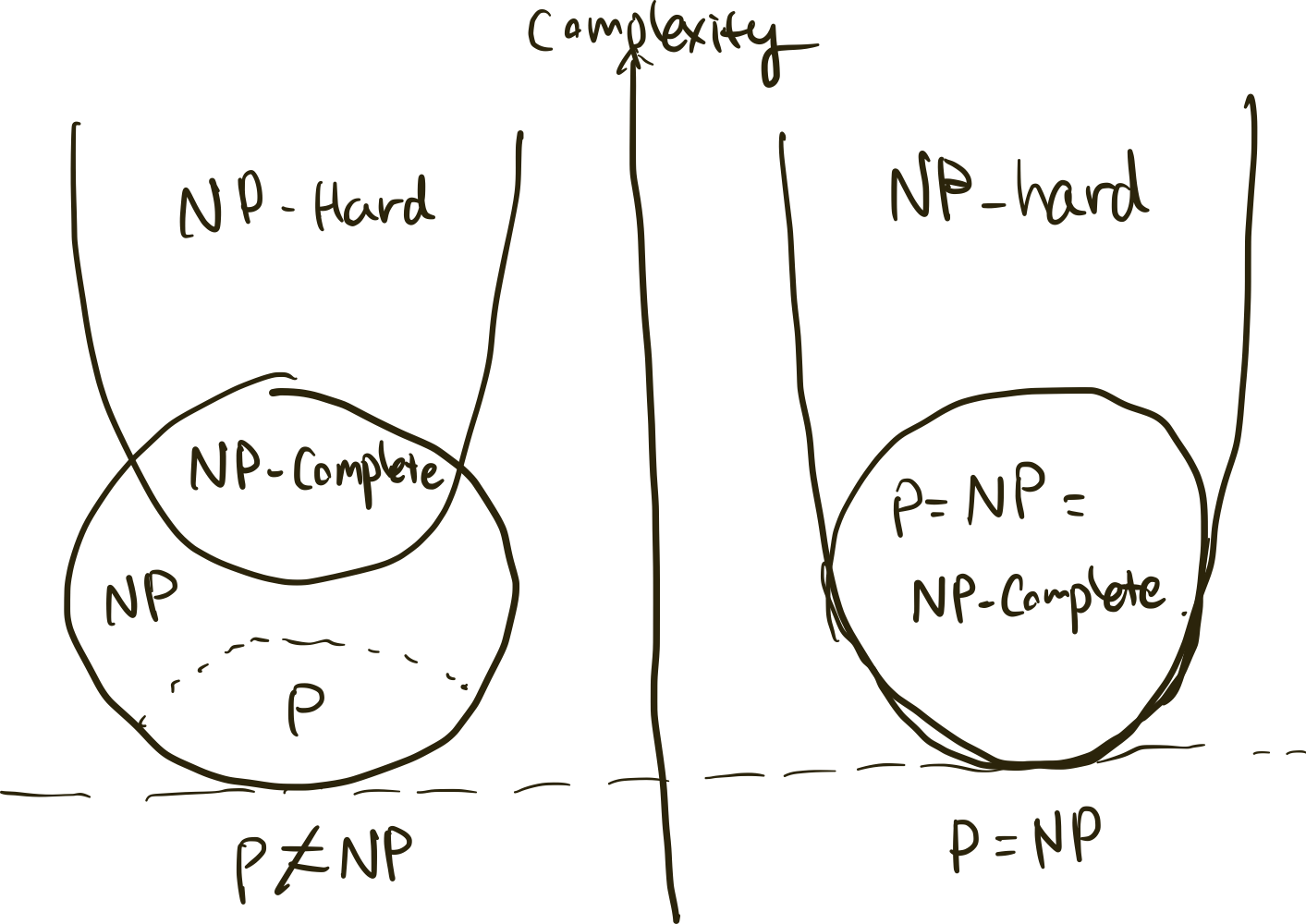
위의 문제는 유명한 P=NP문제에 해당됩니다. 다음 문제를 제기하여 Quantum Computing을 공부해야 하는 이유를 얘기하기 전에, 그림의 각 유형의 문제에 대해 짧게 얘기하겠습니다.

P 문제

이건 DTM을 사용해 Polynomial Time(다항식으로 표현될 수 있는 시간, 변수로 쓰이는 미지수는 Algorithm의 입력 크기이다) 내에 답을 구할 수 있는 문제입니다. 예를 들어 오름차순 배열 문제가 있습니다.

4,2,3,1 을 왼쪽부터 오른쪽으로 오름차순 배열해봅시다.
2,4,3,1
2,3,4,1
2,3,1,4
2,3,1,4
2,1,3,4
1,2,3,4
세 바퀴를 돌아서 끝났습니다. 각 step에 1초가 걸린다면 3+2+1=6초가 걸렸네요.
숫자가 5개면 4+3+2+1=10초가 걸릴 것입니다.
n개면 $n(n-1) \over 2$초가 걸리겠네요. 즉 n에 대한 2차식(다항시간)입니다. 대부분의 polynomial algorithm은 시간이 지나면서 더 빨리 하는 방법이 발견된다고 합니다. 실용적으로는, 3차 이하의 algorithm이 현실에서는 유효하다고 하네요.

NP 문제

P문제가 DTM을 사용하였다면, NP문제는 NDTM(Non-deterministic Turing Machine)을 사용하여 Polynomial Time에 답을 낼 수 있는 문제입니다. NDTM은 어떤 state에서 선택지가 1개 이상, 혹은 없을 수도 있는 기계입니다. 이것의 예로는 부분집합을 찾는 문제를 들 수 있겠네요.

{-2, 10, 6, -5, -3} 라는 집합에서 원소의 총합이 0인 부분집합을 찾아봅시다.
우선 그런 부분집합이 있기는 할까요? {-2, 10, -5, -3}으로 존재는 합니다. 일단 숫자 조합을 찾으면, 연산은 3번만 하면 됩니다(Polynomial Time). 그러나 그 숫자 조합을 찾는 과정이 문제입니다.

숫자 조합 찾기는 여러 선택지가 있습니다. 이걸 DTM으로 한다는 것은 모든 부분집합을 점검한다는 뜻이고, 부분집합은 총 2^5=32개로, input이 지수로 들어갑니다.

만약 input이 10개면 어떻게 될까요? NDTM으로는 확인하는 시간은 P시간입니다. 덧셈을 9번만 하면 되니까요. 그러나 DTM으로는 2^10, 지수시간이 필요합니다. 그러나 이런 문제는, 풀리기는 풀리니까 답은 Yes입니다.

co-NP 문제

주어진 답이 no라는 걸 알아내는 문제를 co-NP문제라고 합니다, NP문제는 답이 있기는 하다! 라는걸 Polynomial Time내에 알아내는거였다면, co-NP문제는 Polynomial Time내에 답이 없다는걸 알아내는 것입니다.

NP-hard 문제

모든 NP 문제를 Polynomial Time내에 문제 A로 reduce할 수 있을 때, 그 문제 A가 바로 NP-hard 문제입니다.

예를 들어
문제 1: N개 숫자를 오름차순 정렬
문제 2: N개 숫자 중 가장 작은 숫자 찾기
문제 3: N개 숫자 중 가장 큰 숫자 찾기
문제 4: N개 숫자 중 중간값 찾기

이렇게 4개의 문제가 있을 때, 문제 1만 해결하면 다른 문제도 해결할 수 있습니다. 즉, 문제 2, 3, 4가 문제 1로 reduce됩니다. 이러한 reduction을 polynomial time안에 할 수 있을 때, 저 중 단 한 문제라도 P문제이면 모든 NP문제가 P문제가 됩니다. 즉 다른 NP문제보다 문제 1이 어려워서 NP-hard문제라고 칭합니다. Turing Machine 포스트의 Halting Problem은 답이 없다고 증명이 됐으니 NP에 속하지 않는 NP-hard 문제입니다.

NP-complete 문제

이거는 NP-hard 문제이면서 NP인 문제입니다. 즉, 답이 있는 문재(NP)중 가장 어려운(NP-hard)문제입니다. 풀 수 있는 문제 중 제일 어려운 문제이고, Hamiltonian Path를 구하는 문제가 NP-complete라고 합니다.

P문제도 물론 실용적으로는 낮은 차수만 쓰기는 하지만, NP는 현실적으로 쓰기 힘듭니다. 즉 이러한 분류는 풀기 어려운 문제에 대한 기준점을 제공합니다. 예를 들어 어떤 문제의 Polynomial algorithm을 못 구하겠다고 하면, 이 문제가 P 문제인지 NP 문제인지 먼저 기준점을 제시하는게 그 문제를 어떻게 다룰 지에 대한 단서를 제공할 것입니다.

주어진 암호를 인수분해하는 Factoring 문제는 NP문제이자 co-NP문제입니다. 암호를 만든 사람은 답이 있다면 Polynomial Time내에 풀 수 있겠지만 답을 모르면 DTM으로는 Polynomial Time 내에 풀 수 없다고 알려져 있습니다. 그리고 Peter Shor는 양자컴퓨터의 특징을 사용하여 이 Factoring 문제를 P시간 내로 푸는 알고리즘을 고안했습니다.