[Stat 110] Probability - 2~3강 기록

Story Proofs, Axioms of Probability

Story proof: Proof by interpretation

• $\Large n \choose k$ = $\Large n \choose n-k$ : n개 중에서 k개를 뽑으면 나머지인 n-k 가 정해짐. 따라서, n개 중에서 n-k를 뽑는 것과 같음.

• $n {n-1 \choose k-1}$ = $k {n \choose k}$: n명 중 k명을 뽑아 동아리를 구성 후, k명 중 1명의 대표를 뽑는 문제 or
  대표를 먼저 뽑은 후 k-1명의 동아리원 뽑기

• $\Large {m + n \choose k} \overset{k}{\underset{j=0}{\sum}} {m \choose j} {n \choose k-j}$; [Vandermonde Identity]

  • m명의 그룹과 n명의 그룹이 있다. 이 두 그룹에서 총 k개를 뽑는다.

  

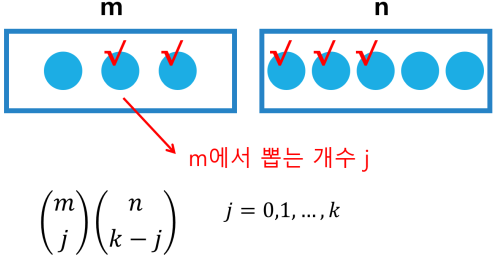
  • m 그룹에서 j개를 선택한다면, n 그룹에서 k-j를 선택해야 함.

  • 중복으로 센 것 없이 모든 다른 경우이므로 전부 더하면 된다.

Non-naive definition

• Probability space(확률공간): S와 P로 구성

  • S = Sample space: 어떤 실험에서 모든 가능한 경우의 수 집합

  • P= Function(어떤 event(사건)을 입력으로 하는 함수)

    • event $A \subseteq S$ as input, returns $P(A) \in [0,1]$ as output

• Axioms (공리)

  0. $0 \leq P(A) \leq 1$

  1. $P(ϕ) = 0$; 공집합에 대한 확률은 0, $P(S) = 1$; 전체 집합에 대한 확률은 1

  2. $P(\cup^{\inf}_{n=1}A_n) = \sum^{\inf}_{n=1} P(A_n)$, if $A_1, A_2, ...$ are disjoint(non-overap)

• Properties

  • $P(A^c) = 1 - P(A)$

    • Proof) $1 = P(S) = P(A \cup A^c) = P(A) + P(A^c)$

  • If $A \subseteq B$, $P(A) \leq P(B)$

    • Proof) $B = A \cup (B \cap A^c)$, disjoint
      • $P(B) = P(A) + P(B \cap A^c) \geq P(A)$
      • (확률은 음수를 가질 수 없음)

  • $P(A \cup B) = P(A) + P(B) - P(A \cap B)$

    • Proof) $P(A \cup B) = P(A \cup (B \cap A^c))$ [disjointicifation]
      • $P(A) + P(B \cap A^c)$
      • $=P(A) + P(B) - P(A \cap B)$, equiv to $P(A \cap B) + P(B \cap A^c) = P(B)$
      • ==> 포함배제의 원리(inclusion-exclusion)

포함배제의 원리(Inclusion-exclusion Principle)

유한 집합의 합집합의 크기를 구할 때, 각 집합의 크기를 단순히 더하는 것이 아니라 중복되는 부분을 고려하여 더하고 빼는 과정을 반복하는 기법

예시) deMontmort's Problem (1713), matching problem

카드가 놓인 위치(첫번째, 두번째, …)와 카드에 쓰여있는 숫자가 일치할 확률

무작위로 섞은 n개의 카드에서, $A_j$ 를 j 번째 카드에 숫자 j가 나오는 사건이라 하면,

구해야 될 확률: $P(A_1 \cup A_2 \cup \cdots \cup A_n)$

• $P(A_j) = \frac{1}{n}$

• $P(A_1 \cap A_2) = \frac{(n-2)!}{n!} = \frac{1}{n(n-1)}$

  • 1번째에 1, 2번째에 2가 나오고 이후는 순서 상관없이 나와도 되므로

• $(A_1 \cap A_2 \cap \cdots \cap A_k) = \frac{(n-k)!}{n!}$

$P(A_1 \cup A_2 \cup \cdots \cup A_n)$
$= P(A_j) \cdot n - P(A_1 \cap A_2) {n \choose 2} + (A_1 \cap A_2 \cap A_3){n \choose 3} - ...$

$= \frac{1}{n} \cdot n - \frac{1}{n(n-1)} {n \choose 2} + \frac{1}{n(n-1)(n-2)}{n \choose 3} - ...$

$= 1-\frac{1}{2!} + \frac{1}{3!} - \cdots + (-1)^n \frac{1}{n!}$ --> 테일러 급수

$\approx 1 - \frac{1}{e}$

Birthday Problem

k명 중에 2명 이상이 같은 생일을 가질 확률

• 가정

  • 윤년 제외, 365일이 모두 동일한 확률 (equaly likely)
  • 독립(모든 사람의 각자 생일이 다른 사람의 생일에 영향을 주지 않음)

if $k > 365$, ==> 1 (Pigeonhole principle)

if $k \leq 365$,

$P(no match) = \frac{365 \cdot 364 \cdots (365-k+1)}{365^k}$

전체 - 모두의 생일이 같지 않을 확률 = 최소한 한 쌍의 생일이 일치할 확률