Probability and Counting
용어 정의
-
표본공간 (sample space): 실험을 통해 나올 수 있는 모든 가능한 결과
-
사건 (event): 표본공간의 부분집합
- : A사건이 일어날 확률
Counting
-
곱의 법칙 (Multiplication Rule):
-
어떤 실험에서 개의 가능한 결과가 있으며, 두 번째에서는 개의 가능한 결과가 ... r 번째에서는 개의 가능한 결과가 있다.
-
여기에서 발생 가능한 모든 경우의 수는
-
트리를 그려서 생각해보면 쉽다
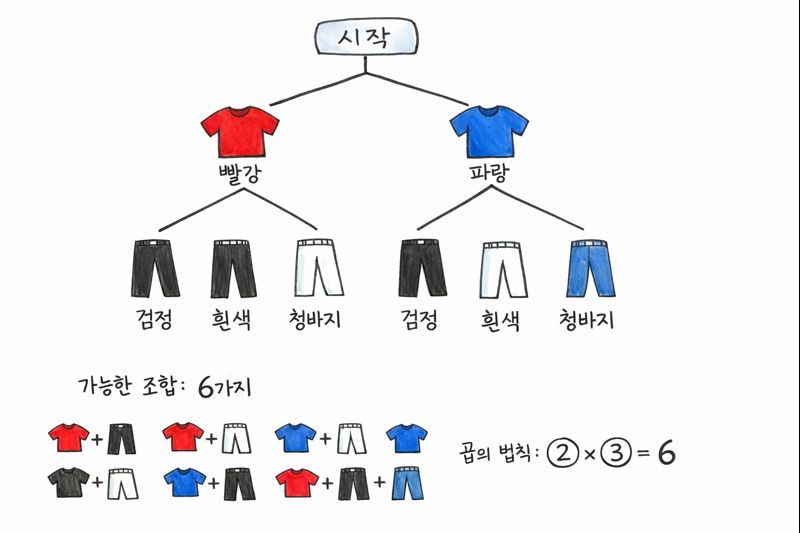
-
-
이항계수(Binomial Coefficient):
=
-
n명의 사람이 있을 때, 그 중k명을 선택하는 경우 -
순서와 상관 없이 크기 n의 집합에서 만들 수 있는 크기 k인 부분집합의 수
- 순서와 상관 없으므로 중복을 제거하기 위해
k!로 나눠줌 (A선택 후 B를 선택하나 B선택후 A를 선택하나 같음)
- 순서와 상관 없으므로 중복을 제거하기 위해
-
-
Sampling Table:
n개 중에k개 뽑기 (경우의 수)- 순서 상관 유무, 대체 유무
- 대체: 선택한 것을 다시 선택 가능order matter order doesn't replace don't replace
- 순서 상관 유무, 대체 유무
(replace, order dosen't matter) 예시 들어 증명하기:
ex) 구별되는 n개의 박스에 구별 안되는 k개 점을 넣는 경우의 수 (n=4, k=6)

위 그림은 다음과 같이 encoding 가능 -->
(박스 사이에 구분자를 추가하는 것으로 바꿈)
이렇게 바꾸면, n-1+k 에서 구분자(n-1) 뽑기 or 점(k)뽑기 문제가 됨
=
