플로이드 워셜 알고리즘

---

✅2차원 테이블 값을 갱신 -> 다이나믹 프로그래밍
✅ O(N^3)이므로 노드 갯수 500개 이하로 문제에서 주어짐 (but, 500^3 = 1억이 조금 넘기때문에 1초가 초과 될 수도 있다)

동작 원리

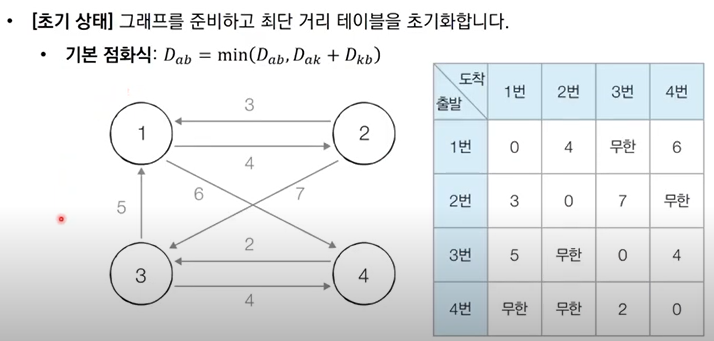✅ 2->4로 가는 간선이 없으므로 무한✅ 하늘색 칸 -> 갱신 가능 영역

• 1번 노드를 "거치는" 경우만 따지므로 1행 및 1열은 갱신되지 않음 (k=1이면, a와 b는 1이 아님)
• 자기자신->자기자신으로 가는 경우는 갱신되지 않음

소스

import java.util.*;

public class Main {

    public static final int INF = (int) 1e9; // 무한을 의미하는 값으로 10억을 설정
    // 노드의 개수(N), 간선의 개수(M)
    // 노드의 개수는 최대 500개라고 가정
    public static int n, m;
    // 2차원 배열(그래프 표현)를 만들기
    public static int[][] graph = new int[501][501];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        n = sc.nextInt();
        m = sc.nextInt();

        // 최단 거리 테이블을 모두 무한으로 초기화
        for (int i = 0; i < 501; i++) {
            Arrays.fill(graph[i], INF);
        }

        // 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
        for (int a = 1; a <= n; a++) {
            for (int b = 1; b <= n; b++) {
                if (a == b) graph[a][b] = 0;
            }
        }

        // 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
        for (int i = 0; i < m; i++) {
            // A에서 B로 가는 비용은 C라고 설정
            int a = sc.nextInt();
            int b = sc.nextInt();
            int c = sc.nextInt();
            graph[a][b] = c;
        }

        // 점화식에 따라 플로이드 워셜 알고리즘을 수행
        // k : 거쳐가는 노드
        for (int k = 1; k <= n; k++) {
        	// 모든 a에서 모든 b로 가는 경우 
        	// a : 출발 노드
            for (int a = 1; a <= n; a++) {
            	// b : 도착 노드
                for (int b = 1; b <= n; b++) {
                    graph[a][b] = Math.min(graph[a][b], graph[a][k] + graph[k][b]);
                }
            }
        }

        // 수행된 결과를 출력
        for (int a = 1; a <= n; a++) {
            for (int b = 1; b <= n; b++) {
                // 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
                if (graph[a][b] == INF) {
                    System.out.print("INFINITY ");
                }
                // 도달할 수 있는 경우 거리를 출력
                else {
                    System.out.print(graph[a][b] + " ");
                }
            }
            System.out.println();
        }
    }
}

성능 분석

✅ N번의 단계 ~ : K에 대한 설명 (거쳐가는 노드)