투 포인터 알고리즘

예제

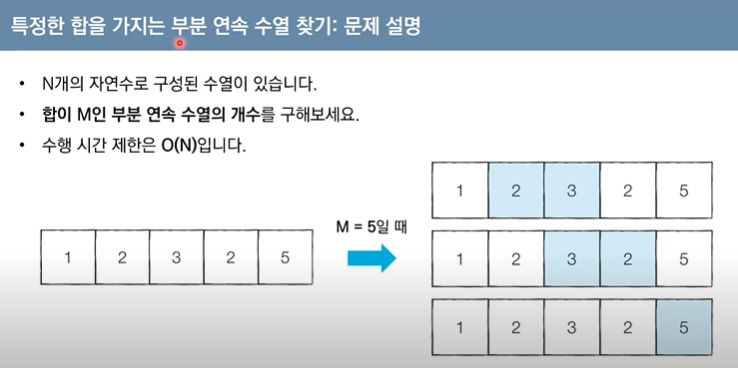✅ 부분 연속 수열 : 하나의 수열 안에서 연속된 일부 데이터들로 구성된 수열
✅ 간단히 완전탐색으로 해결한다면 O(N^2) 소요

외부 for문 1(시작) -> 합이 M이 될 때 까지 내부 for문 2, 3, 2, 5 순회
외부 for문 2(시작) -> 합이 M이 될 때 까지 내부 for문 3, 2, 5 순회
외부 for문 3(시작) -> 합이 M이 될 때 까지 내부 for문 2, 5 순회
외부 for문 2(시작) -> 합이 M이 될 때 까지 내부 for문 5 순회
외부 for문 5(시작) -> 순회 X
=> 4 + 3 + 2 + 1 + 0 => O(N^2)

동작 원리

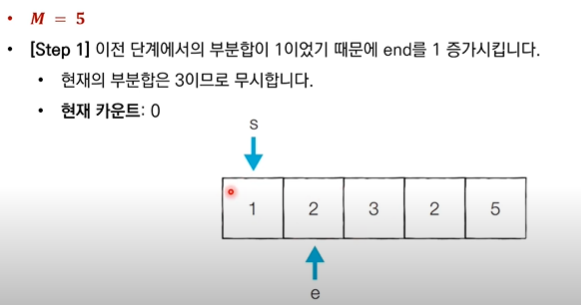
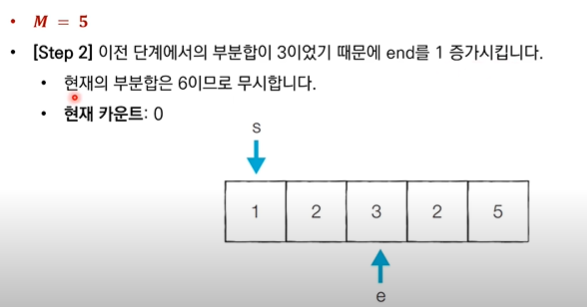
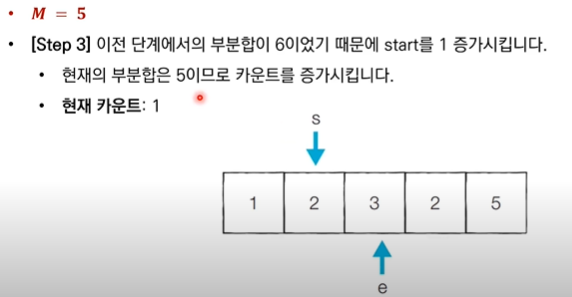
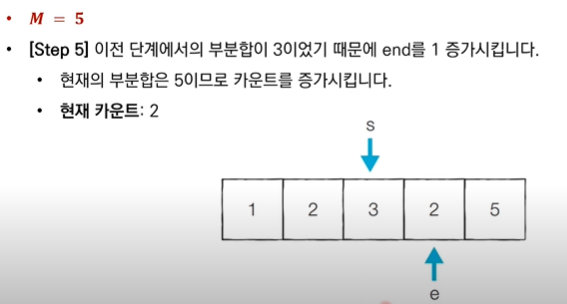
✅ "end를 1 증가시킨다." : 현재 부분합이 M보다 작기 때문에, 현재 부분합을 증가시키기 위해 end를 증가(범위 늘리기)시킨다.
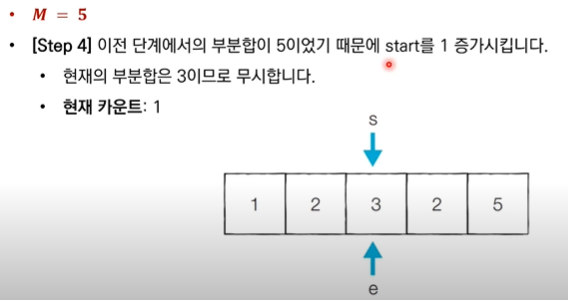
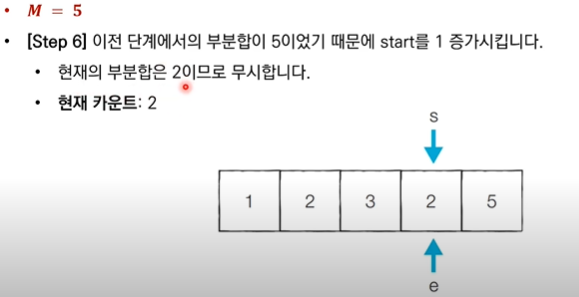
✅ "start를 1 감소시킨다." : 현재 부분합이 M보다 크기 때문에, 현재 부분합을 감소시키기 위해 start를 감소(범위 줄이기)시킨다.
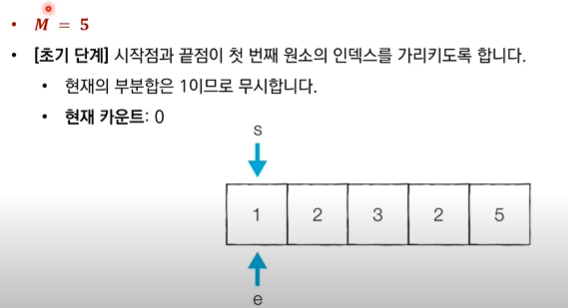✅ "무시합니다" : 카운트를 진행하지 않는다.

소스

import java.util.*;

class Main {
    public static int n = 5; // 데이터의 개수 N
    public static int m = 5; // 찾고자 하는 부분합 M
    public static int[] arr = {1, 2, 3, 2, 5}; // 전체 수열

    public static void main(String[] args) {
        int cnt = 0;
        int intervalSum = 0;
        int end = 0;

        // start를 차례대로 증가시키며 반복
        for (int start = 0; start < n; start++) {
            // end를 가능한 만큼 이동시키기
            while (intervalSum < m && end < n) {
                intervalSum += arr[end];
                end += 1;
            }
            // 부분합이 m일 때 카운트 증가
            if (intervalSum == m) {
                cnt += 1;
            }

            // intervalSum >= m
            intervalSum -= arr[start];
        }

        System.out.println(cnt);
    }
}

for문 안에 while문이 있는데, O(N)인 이유
안쪽 while 문은 프로그램이 시작되어 종료될동안 총 n번 반복한다. lt가 0부터 n까지 증가하는 동안만 반복하는 것이기 때문. 따라서 for문에서 총 n번, while문에서 총 n번이므로 N+N => 2N => O(N)