구간 합 빠르게 계산하기

✅ 구간합을 구하는 행위가 한번만 이루어진다면, 선형탐색(ex. for(i=2; i=<4; i++))으로 구하면 되지만 쿼리 개수만큼 여러번 구해야한다면 O(N * M)만큼의 시간복잡도 소요

O(N * M)인 이유
최악의 경우 M개의 쿼리 모두 1~5까지의 합을 구한다고 하면,
for(i=1; i=<5; i++) 5번 씩 쿼리 개수 M만큼의 연산이 수행된다

예제

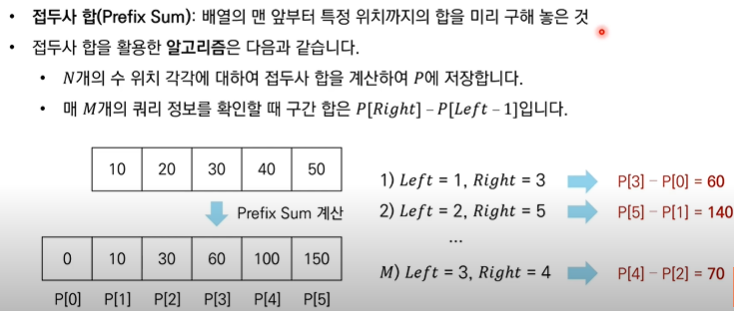
전략

소스

import java.util.*;

class Main {
    public static int n = 5; // 데이터의 개수 N과 데이터 입력받기
    public static int arr[] = {10, 20, 30, 40, 50};
    public static int[] prefixSum = new int[6];

    public static void main(String[] args) {
        int sumValue = 0;

        // 접두사 합(Prefix Sum) 배열 계산
        // O(N)
        for (int i = 0; i < n; i++) {
            sumValue += arr[i];
            prefixSum[i + 1] = sumValue;
        }

        // 구간 합 계산(세 번째 수부터 네 번째 수까지)
        // 쿼리 하나 당 상수시간 O(1) 소요 * 쿼리 개수 M => O(M)
        int left = 3;
        int right = 4;
        System.out.println(prefixSum[right] - prefixSum[left - 1]);
    }
}