기계 학습
컴퓨터가 경험, 예, 유추 등을 통해 학습할 수 있도록 컴퓨터에 학습 능력을 부여하기 위해 연구하는 분야
학습 능력은 시간이 흐름에 따라 지능형 시스템의 성능을 개성
ex) 체스 프로그램과 학습 능력
딥 블루와 체스 게임 선수의 체스게임 -> 경험학습 능력은 아니다.
딥블루 - IBM에서 만든 초당 2억개의 포지션을 분석할 수 있는 컴퓨터
기계 학습의 접근법
- 인공 신경망 (artificial neural network)
- 유전 알고리즘 (genetic algorithm)
학습의 분류
-
암기 학습 - 지식을 통해 database에 지식저장
-
지도에 의한 학습 - 교사의 객체의 지식
-
유추에 의한 학습 - 과거의 유사한 경험을 통해 유사점과 차이점을 통해 학슴
-
강화학습 - 제일많이쓰인다. ex)미로학습
-
예를 통한 학습 - 어떤 개념 묘사를 위해 제공된 긍정적인 사례와 부정적인 사례들로부터 긍정적인 사례들에 대한 개념 습득
귀납저 학습의 특수한 경우 강화학습과 양대산맥이다 -
관찰을 통한 학습 - 귀납적 학습의 일반적인 형태
예제들의 긍정,부정에 대한 정보도 없음-> 무감독 학습 ex) 사례를 강아지인지 고양이인지 알려주지 않음
발견 시스템, 이론 형성 작업, 분류 계층 형성을 위한 분류 기준 생성 - 특징에 따라 분류
인공 신경망
인간 뇌를 기반으로 한 추론 모델
인간의 뇌 -- 신경세포(neuron)의 집합
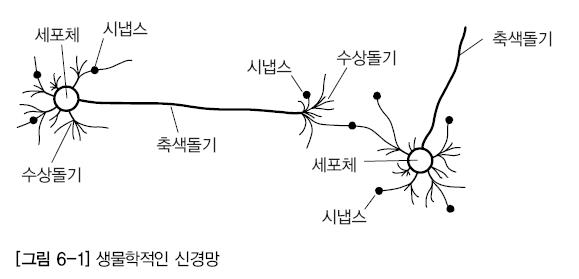
시냅스가 연결부위이다.
뉴런은 기본적인 정보처리 단위
인공 신경망의 주요 특징들은 적응성을 가지고있다는 것이다.
인간 뇌의 특징
100억개늬 뉴런과 각 뉴런을 연결하는 6조개의 시냅스 결합체
현존하는 어떤 컴퓨터보다 빠르게 기능 수행 가능
매우 복잡, 비선형적, 병렬적인 정보처리 시스템으로 생각할 수 있다.
뉴런들 사이의 연결 강도는 자극 패턴에 반응하여 장기적인 변화, 즉 적응성을 나타냄
적응성에 따라 '잘못된 답'으로 이끄는 뉴런들 사이의 연결은 약화되고 '올바른 답'으로 이끄는 연결은 강화된다 => 경험을 통한 학습 능력을 가짐
인공 신경망의 특징 (학습 알고리즘)
인간 뇌를 기반으로 모델링
인간 뇌의 적응성을 활용하여 '학습 능력'을 구현
인공 신경망은 아직 인간의 뇌를 흉내내기에 미흡
인공 신경망 모델링
인간의 뇌 모델링
뇌의 뉴런과 비슷하게 모델링
뉴런이라는 아주 단순하지만 내부적으로 매우 복합하게 연결된 프로세스로 이루어려있다.
뉴런은 가중치 있는 링크들로 연결되어 있다.
각각의 뉴런은 연결을 통해 여러 입력 신호를 받지만 출력 신호는 '오직 하나만' 만듦
가중치를 정하는게 가장 중요 => 이것을 학습과정이라고 한다.
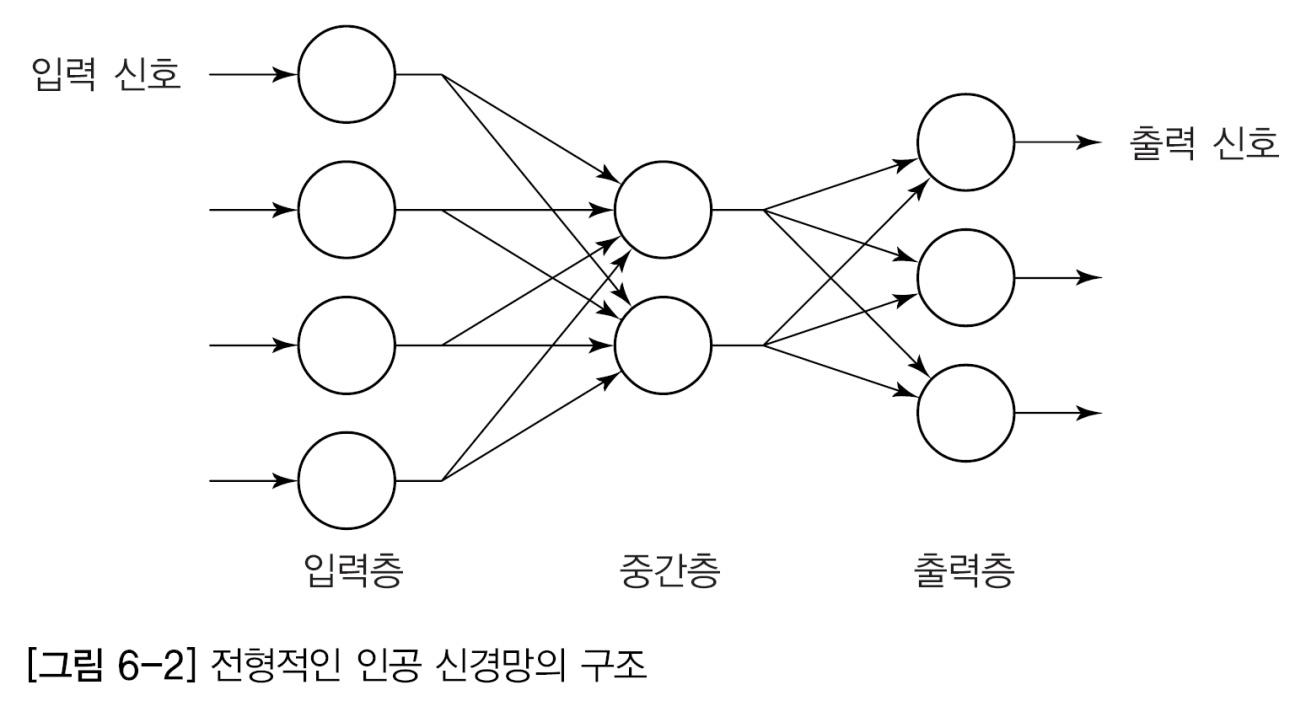
입력값 + 가중치로 연산 수행후 출력값을 결정
인공 신경망의 학습
신경망은 가중치를 반복적으로 조정하여 학습
뉴런은 링크로 연결되어있고 각 링크에는 그와 연관된 수치적인 가중치가 있다.
가중치는 장기 기억을 위한 기본적인 수단으로, 각 뉴런 입력 강도, 즉 중요도를 표현
인공 신경망의 가중치 조정
신경망의 가중치를 초기화하고 훈련 예제들의 집합에서 해당 가중치 갱신
신경망의 구조를 먼저 선택하고, 어떤 학습 알고리즘을 사용할 것 인지 결정한 후 훈련시킨다.
뉴런의 특징
입력 링크에서 여러 신호를 받아서 새로운 활성화 수준을 계산하고, 출력 링크로 출력 신호를 내보낸다.
입력 신호는 미가공 데이터 또는 다른 뉴런의 출력이 될 수 있다.
출력 신호는 문제의 최종적인 해(solution)거나 다른 뉴런에 입력될 수 있다.
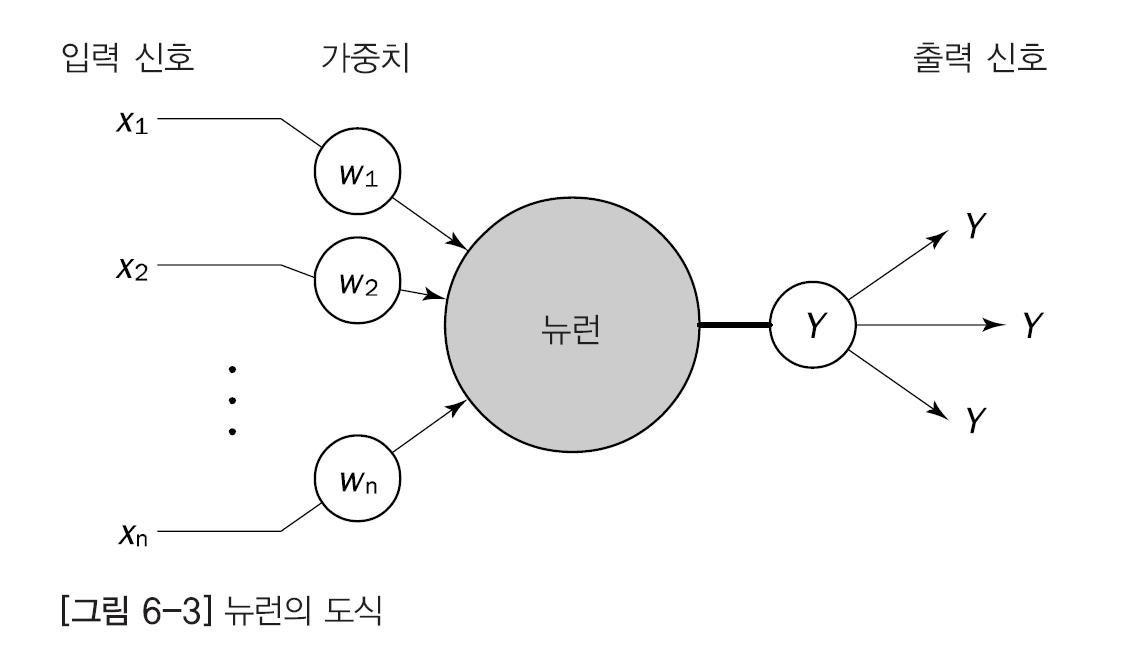
입력층 중간층 출력으로 이루어져있다.
출력신호가 문제의 최종적인 해
뉴런의 계산
렌 맥클록과 월터 피르가 제안한 뉴런의 출력 결정 (1943년).
뉴런은 당므과 같은 전이 함수, 즉 활성화 함수를 사용
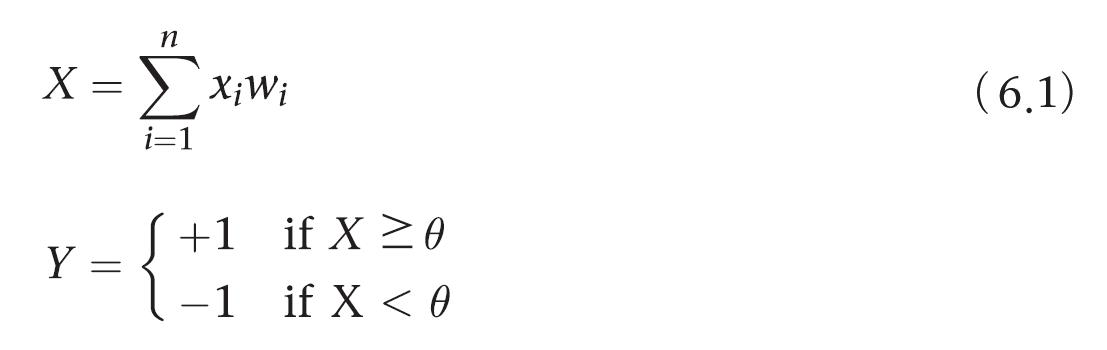
입력값 X 가중치
세타 -> 임계치
x는 뉴런으로 들어가는 입력의 순 가중합
n은 뉴런의 입력 개수, y는 뉴런의 출력
활성화 함수를 이용한 출력 결정 순서
- 뉴런은 입력 신호의 가중치 합을 계산하면 임계값 세타와 비교한다.
- 가중치 합이 임계값보다 작으면 뉴런의 출력은 -1이다.
- 가중치 합이 임계값과 같거나 크면 뉴런은 활성화되고 뉴런의 출력은 +1이 된다.
뉴런의 출력 결정
위의 같은 활성화 함수를 부호 함수라고 한다.
부호 활성화 함수를 사용하는 뉴런의 실제 출력 식

뉴런의 활성화 함수
가장 일반적인 활성화 함수로는 계단, 부호, 선형, 시그모이드 함수가 있다.
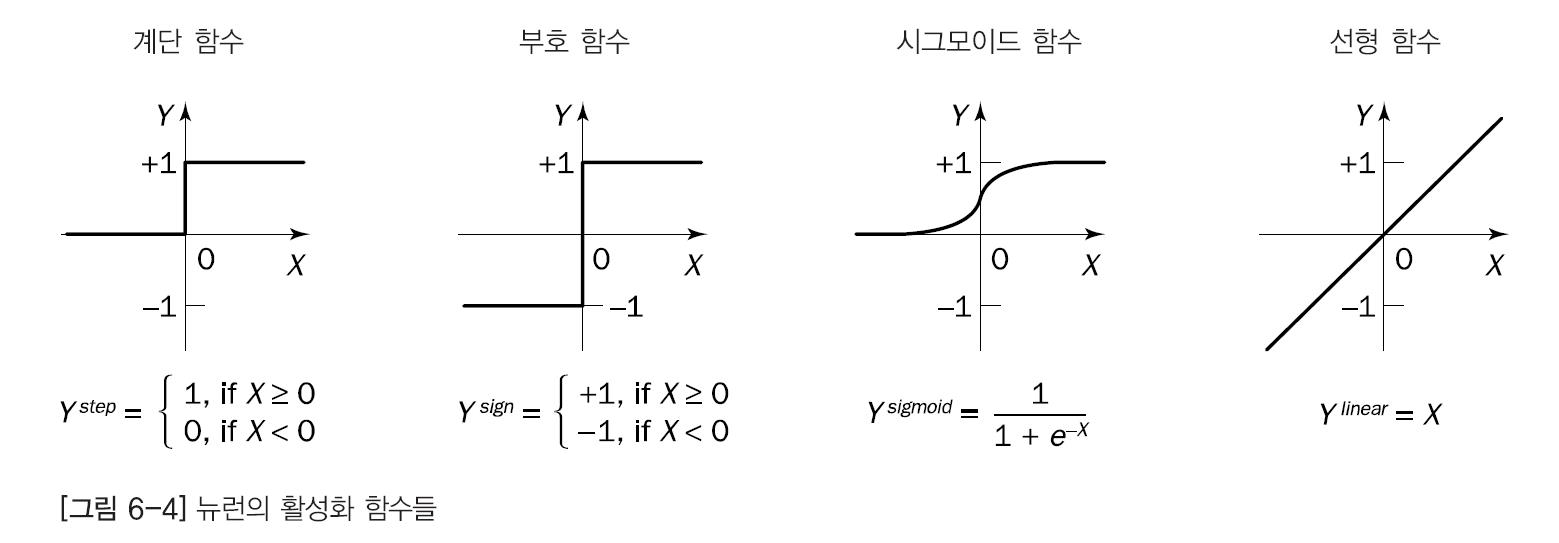
시그 모이드 함수가 가장 많이 쓰인다!
계단(step)과 부호(sign) 활성화 함수 - 하드리밋 함수 라고도 하며 분류와 패턴 인식 작업에서 결정을 내리는 뉴런에 주로 쓰임
시그모이드 함수 - 양과 음의 무한대 사이에있는 입력값 0~1사이에 있는 적당한 값으로 바꾼다. 역전파 신경망에 쓰인다.
선형 활성화 함수 - ㄴ런의 입력에 가중치가 적용된 것과 같은 값을 출력으로 내놓는다. 선형 함수를 사용하는 뉴런은 선형 근사에 주로 쓰인다.
정규화 선형 함수 - 심층 신경망에서 많이쓰임
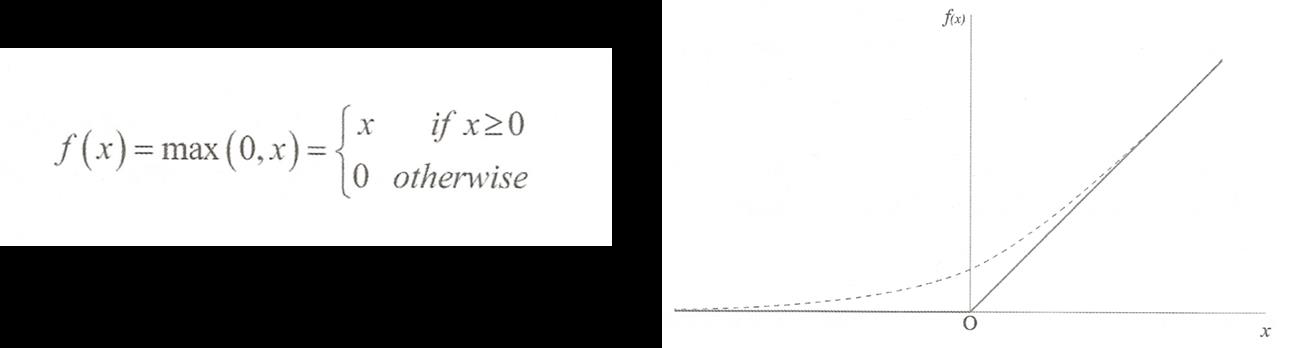
0보다 작으면 0 이고 그의외는 그대로 출력
퍼셉트론
단일 뉴런 학습- 퍼센트론
프랭크 로젠블랫이 간단한 인공신경망을 훈련시키기 위해 퍼셉트론 알고리즘을 소개했다(1958)
퍼센트론은 신경망의 가장 간단한 형태로 조정 가능한 시냅스 가중치와 하드리미터를 포함한 단일 뉴런으로 구성된다. - 적절한 가중치를 학습
입력 노드가 두개인 단층 퍼셉트론
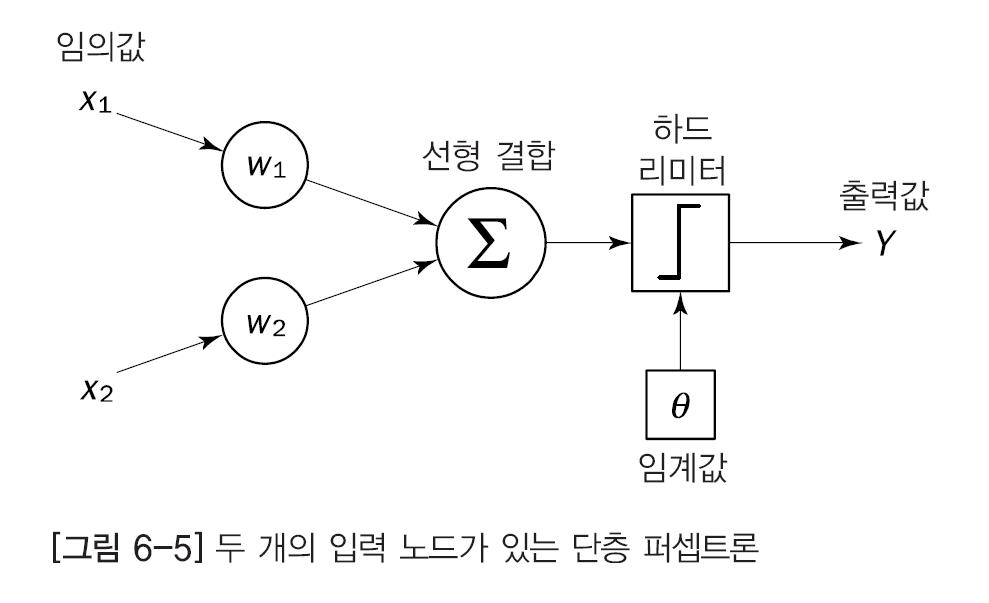
퍼셉트론의 특징
로젠블랫 퍼셉트론의 동작 원리는 맥클록과 피츠의 뉴런 모델에 기반.
퍼셉트론은 선형 결합기와 하드 리미터로 구성
입력의 가중합을 하드 리미터에 입력하고 입력이 양이면 +1 음이면 -1을 출력
기본적인 퍼셉트론의 경우 식의 선형분리 함수로 정의된 초평면으로 n차원 공간의 두개의 결정 영역으로 나뉜다.

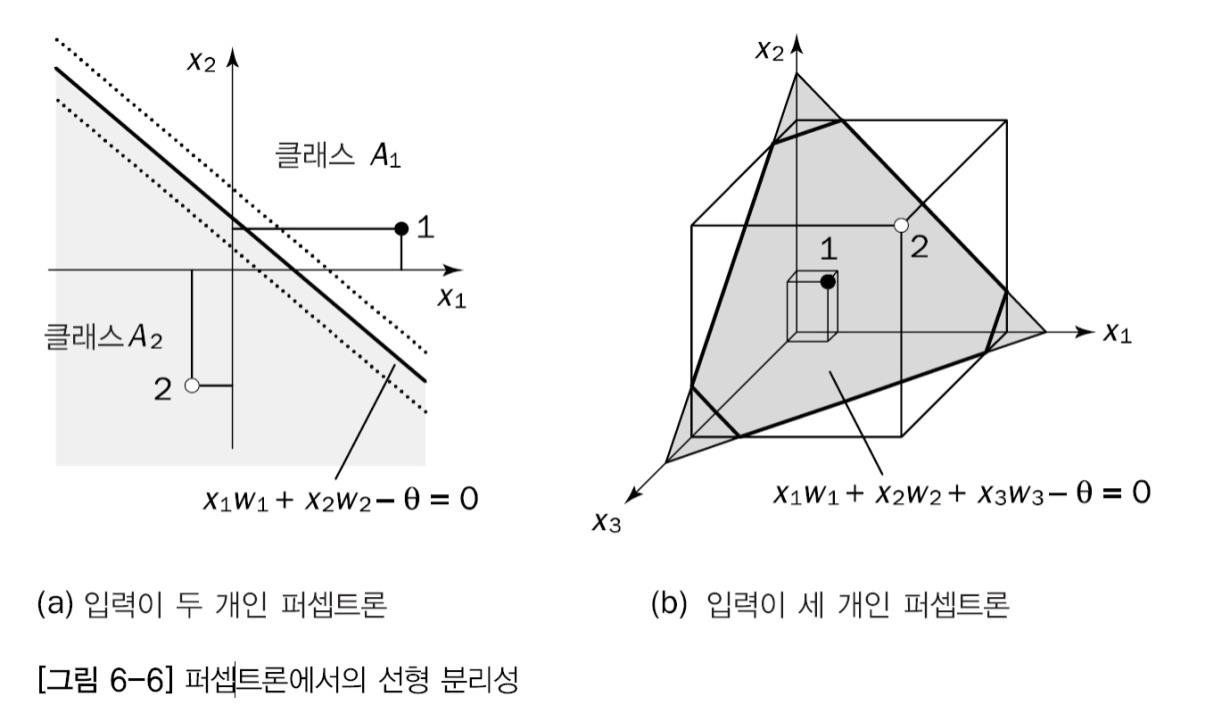
입력이 x1 과 x2로 두개일때 결정 경계는(a)에 보이듯 굵은 직선 형태로 나타냄
경계선 오른편에 있는 점 (1)은 클래스 A1에 속하고 왼편에 있는점 (2)는 A2에 속한다.
임계값 세타는 결정 경계를 옮기는데 쓰임
분할식
입력이 두개인 퍼셉트론 x1w1 + x2w2 -θ =0
입력이 세 개인 퍼셉트론 x1w1 + x2w2 + x3w3 -θ = 0
퍼센트론 기본 학습 방법
가중치를 조절하여 실제 출력과 목표 출력 간의 차이를 줄인다.
보통 [-0.5, 0.5] 범위에서 초기 가중치를 임의로 할당한 후 훈련 예제와 일치하는 출력을 얻로고 갱신
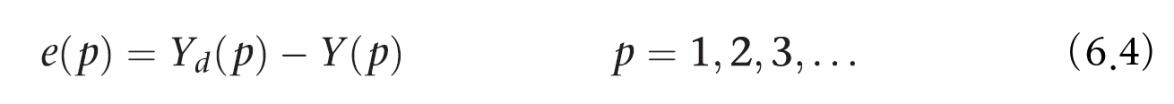
오차 계산식
p번째 반복, 실제 출력이 Y(p)이고 목표 출력 Yd(p)
오차 e(p)가 양 - 퍼셉트론의 출력 Y(p)f를 증가시켜야한다. 긍정을 부정으로 분류한 case
오차 e(p)가 음 - Y(p)를 감소시킨다 - 부정을 긍정으로 분류한 case
퍼셉트론 학습 규칙
로젠블랫이 제한(1960년대)
오차 e(p)를 이용
e(p) > 0 퍼센트론의 출력 Y(p)를 증가
e(p) < 0 Y(p)를 감소
각 퍼셉트론의 입력에 대해 x(p) X w(p) 값이 총합 X(p)에 기여한다는 것을 고려하면,
x(p)가 양일때 가중치 w(p)가 커지면 Y(p)도 커진다.
x(p)가 음일때 가중치 w(p)가 커지면 Y(p)가 줄어든다.
퍼셉트론 학습 규칙 식
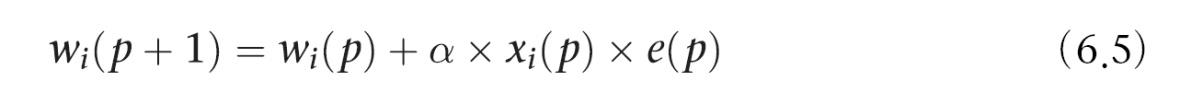
알파는 학습률로 1보다 작은 양의 상수
오차 음수 입력 음수 -> 가중치 증가
오차가 0보다 크면 긍정을 부정이라고 분류 - 가중합 늘려야됨
오차가 0보다 작으면 부정을 긍정으로 분류 - 가중합 줄여야됨 !!! 잘 기억하자
퍼센트론 훈련 알고리즘
1단계 : 초기화
초기 가중치 w1,w2...wn과 임계값 θ를 [-0.5, 0.5] 구간의 임의의 값으로 설정
2단계 : 활성화
입력 x1(p), x2(p) ...xn(p)와 목표출력 Yd(p)를 적용하여 퍼셉트론을 활성화
반복 횟수 p = 1 에서 실제 출력을 계산
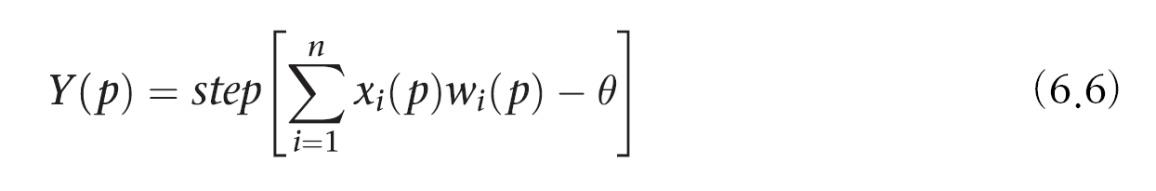
n은 퍼셉트론의 입력 개수, step은 계단 활성화함수
3단계: 가중치 학습
퍼셉트론의 가중치를 갱신한다.
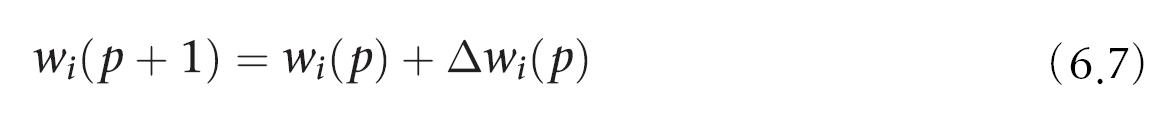
Δwi(p)는 p번째 반복했을 때의 가중치 보정값. 가중치 보정값은 델타 규칙(delta rule)으로 계산한다.
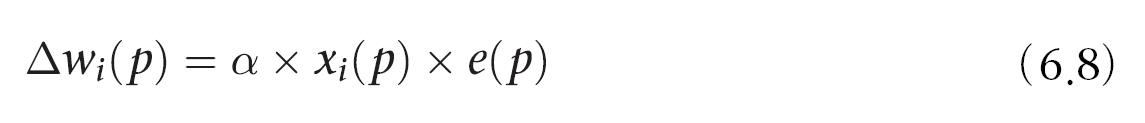
4단계: 반복
반복 횟수 p값을 1증가 시키고 2단계로 돌아가서 수렴할 때까지 반복한다.
기본적인 논리 연산자 학습
AND OR EXCLUSIVE-OR와 같은 기본적인 논리 연산자의 기능을 수행하도록 훈련
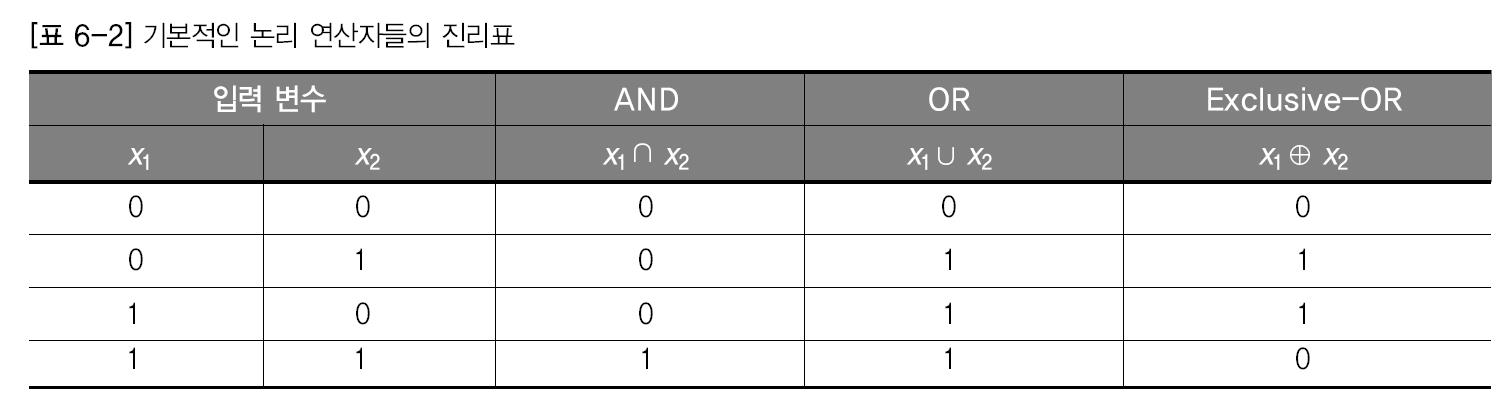
AND 와 OR 연산자 학습
학습 순서
1. 하나의 에폭(사례를 전부 사용하면 4개 = 1에폭) 나태대는 네 개의 연속된 입력 패턴트로 퍼셉트론을 활성화한다.
2. 퍼셉트론의 가중치는 각각의 활성화 이후에 갱신된다.
3. 가중치가 일관된 수치 집합으로 수렴할 때까지 이과정을 반복
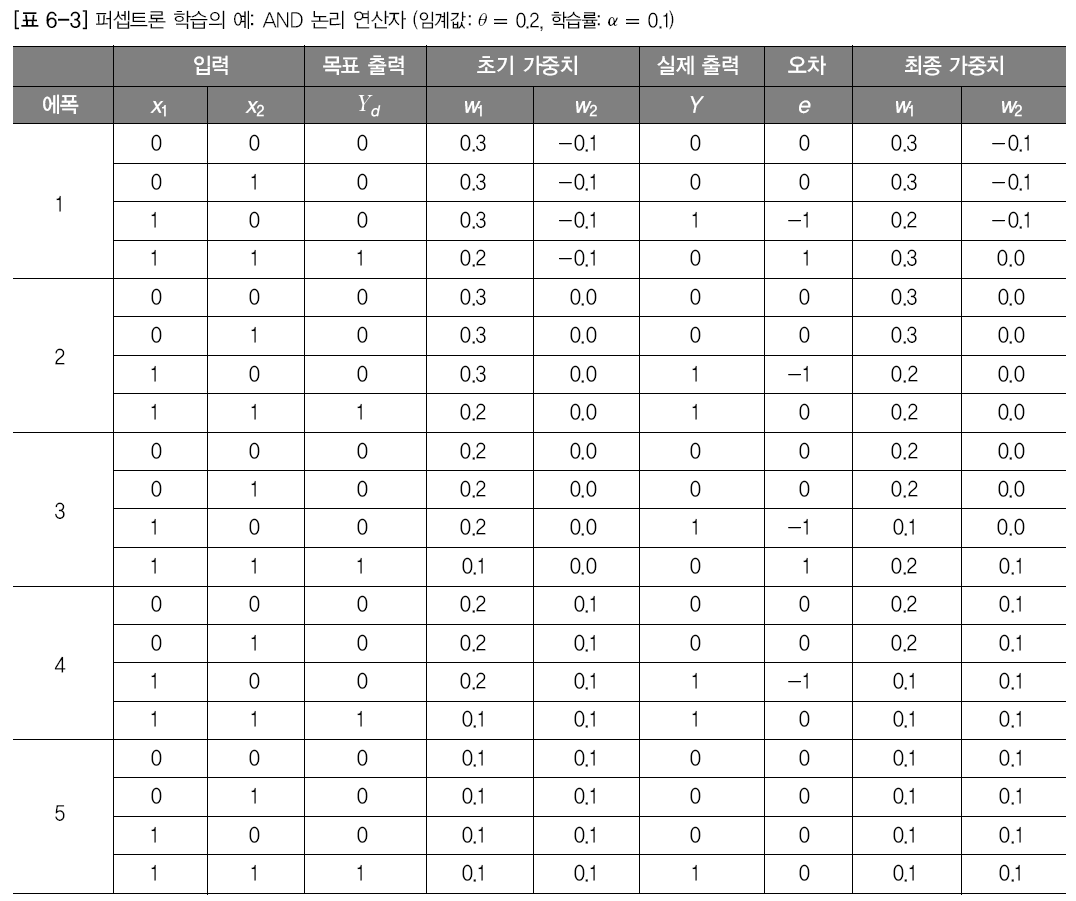 학습 결과
학습 결과
초기 가중치는 0.3과 -0.1
분류 결과에 따라서 가중치를 조정하는 과정을 반복한다.
1에폭 3번째 에서 목표출력은 0이지만 실제출력은 1이다. 오차는 -1 위의 식 6-5에 따라서 가중치를 조절하면 0.2와 -0.1이 나오는것이다.
이런식으로 계속 반복
5번째 에폭에서 가중치는 0.1 0.1이 되고 이때 모든 사례를 올바르게 분류하기 때문에 학습을 끝낸다.
Exclusive -OR 연산자 학습
단층 퍼셉트론으로 학습할 수 없다.
why? 선행 분리가 불가능 하기 때문에
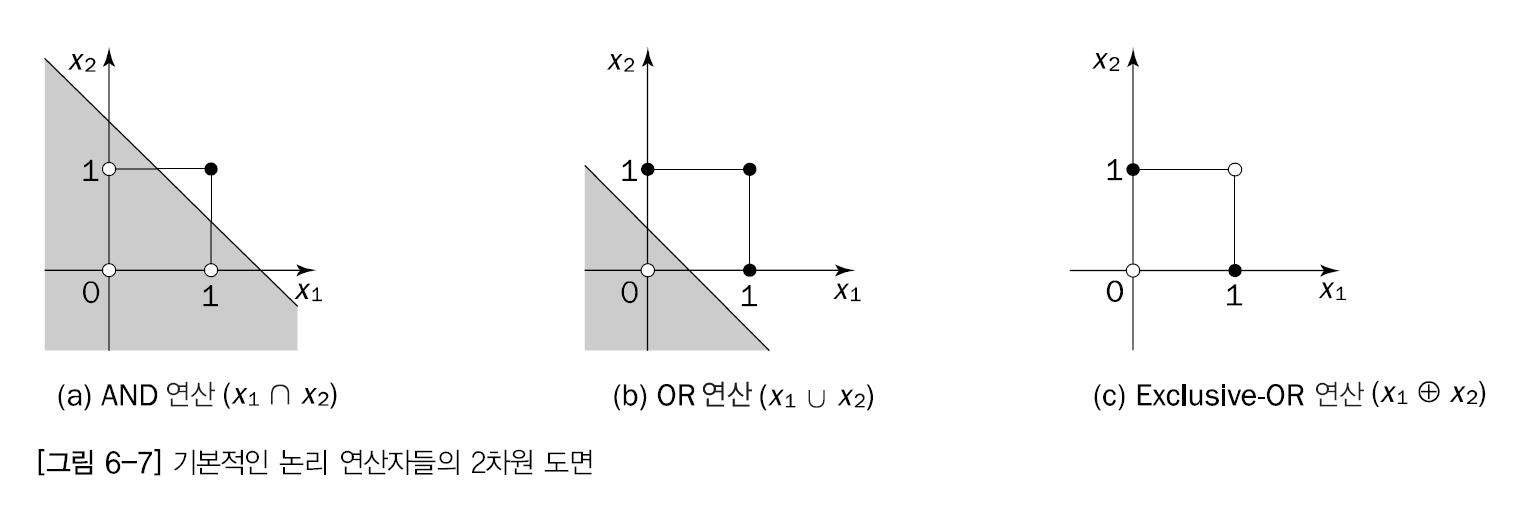
함수의 출력이 1인 입력공안의 점은 검은색 출력이 0인 점은 흰색
- (a)와 (b)에서는 검은 점과 흰 점을 구분하여 직선을 그릴 수 있지만, (c)의 점들은 직선으로 분리할 수 없다.
- 퍼셉트론은 모든 검은 점과 모든 흰 점을 분리하는 직선이 있을 때만 함수로 표현할 수 있다.
단층 퍼셉트론 학습의 한계
only 선형 분리 가능한 함수한 학습할 수 있다.
선행 분리 가능한 함수들이 많지 않기 때문에 그리 좋지 않다.
한계 극복
다층 신경망으로 단층 퍼셉트론을 극복할 수 있다.
역전파 알고리즘으로 학습한 다층 퍼셉트론처럼 형태의 신경망을 사용하면 로젠블랫 퍼셉트론의 한계를 극볼할 수 있다는 것이 증명되었다.
다층 신경망은 다음에 !!
