인공지능 - 퍼지 전문가 시스템2

저번에 이어서 스게노형 추론부터

스게노형 추론

일본의 스게노 미치오가 1985년에 도입

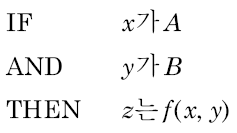
x,y,z 는 언어 변수이고, A,와 는 논의 영역 X와 Y로 하는 퍼지 집합이다.

f(x,y)는 수학함수, 스게노는 규칙 후건에 퍼지집합 대신 입력 변수에 대한 수학 함수를 하용한다.

0차 스게노 모델의 퍼지 규칙

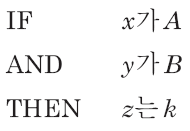
k는 상수

이경우에 각 퍼지 규칙의 출력은 상수이다.
모든 후건 소속 함수를 단일체로 표현, 단일체는 소속 함수가 논의 영역 위의 특정 점에서는 1이고 다른 모든 점에서는 0인 퍼지 집합이다.

스게노형 퍼지 추론의 기본 구조

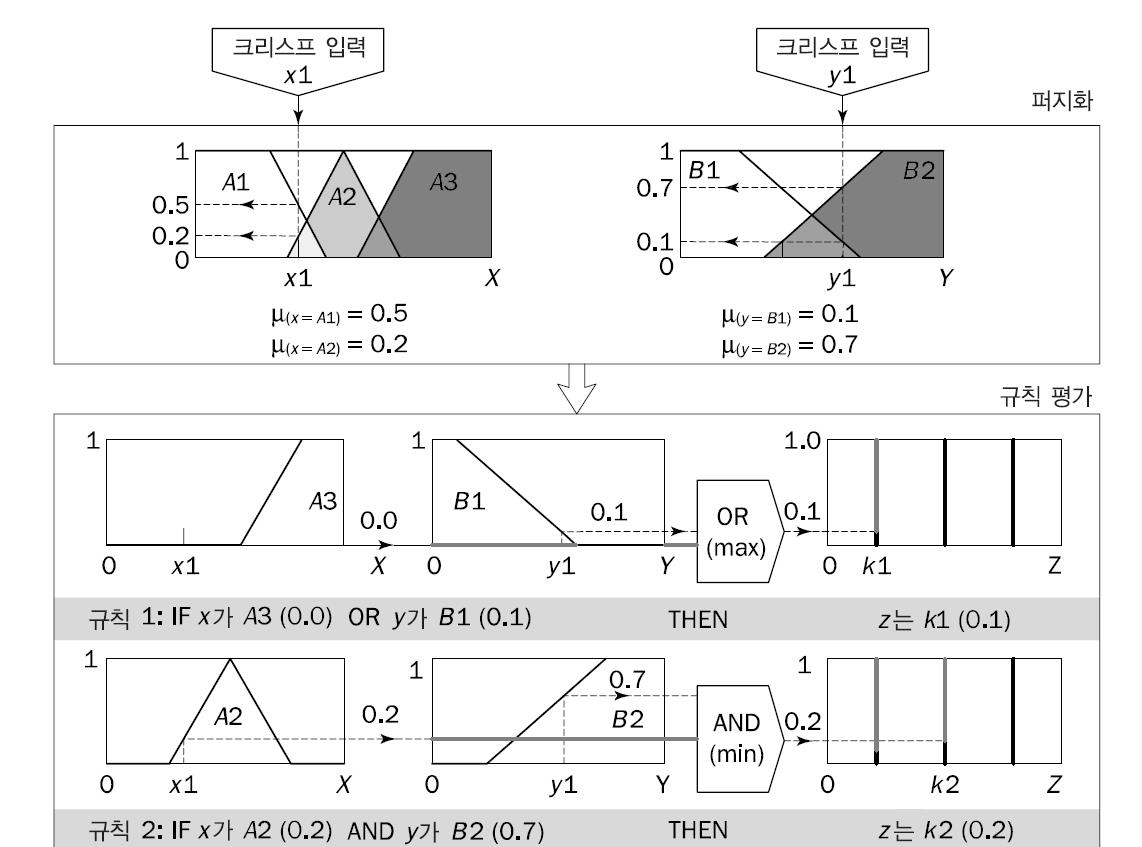
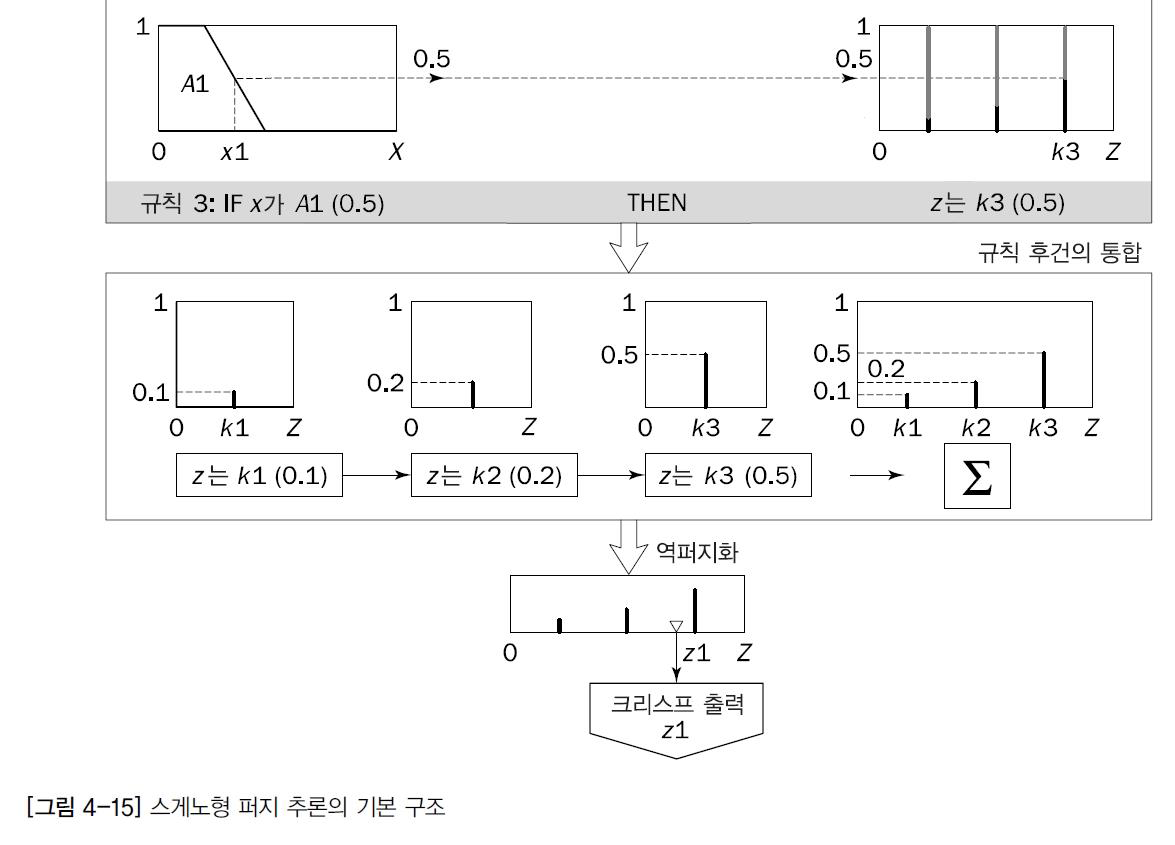
낮다 보통이다 이런 방식이 아니라, 상수를 사용한다.
전근의 평가 결과 x 후건의 상수값
평가 결과 0.1 x k
0.2 x k2

평가결과 - 0.5 x k3

크리스프 출력를 얻는 방법

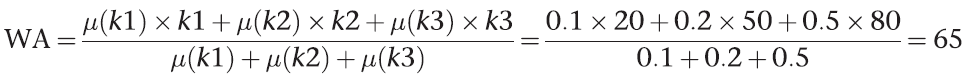
출력은 단일체의 가중평균으로 구한다.

스게노 규칙은 효율적인 계산이 나온다. 역퍼지화가 빠르다.

맘다니 vs 스게노

맘다니 방법은 전문 지식을 더욱 직관적이고 인간의 방식으로 설명할 수 있다.

• 전문가의 지식을 얻는데 많이 사용됨

but!- 맘다니형 퍼지 추론은 계산 비용이 많이든다.
why? - 퍼지집합을 다루기 때문에

스게노 방법은 계산을 효울적으로 할 수 있고, 최적화나 적응형 기법과 함께 잘 작동한다.

• 제어 문제, 특히 동적 비선형 시스템에서 매우 매력적이다.

  퍼지 전문가 시스템 구축

  퍼지 전문가 시스템은 퍼지 집합과 퍼지 규칙을 정의한 다음, 정해진 요구 조건에 따라 시스템을 평가하고, 조정하는 작업을 반복하는 과정을 통해 구축

퍼지 전문가 시스템 개발 절차

1. 문제를 명확히 하고 언어 변수를 정의한다.
2. 퍼지 집합을 결정한다.
3. 퍼지 규칙을 구성하고 도출한다.
4. 퍼지 집합, 퍼지 규칙, 퍼지 추론을 수행하는 절파를 퍼지 시스템에 부호화해 넣는다.
5. 시스템을 평가하고 조정한다.

조정이 시스템 구축에서 가장 힘들고 지루한 부분

1단계: 문제를 명확히 하고 언어 변수를 정의

문제의 입출력 변수와 그 범위를 결정한다.

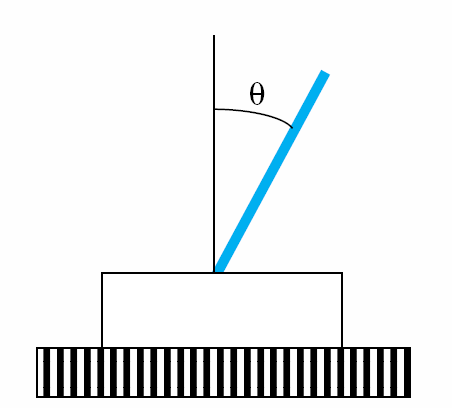
예시 문제 - 나무막대 손바닥위에 쓰러지지 않게 하는거와 같은 문제

2단계: 퍼지 집합을 결정

퍼지 집합은 다양한 형태를 띤다.
그러다 삼각형이나 사다리꼴은 전문지식을 나타내기 좋고 계산과정이 간편

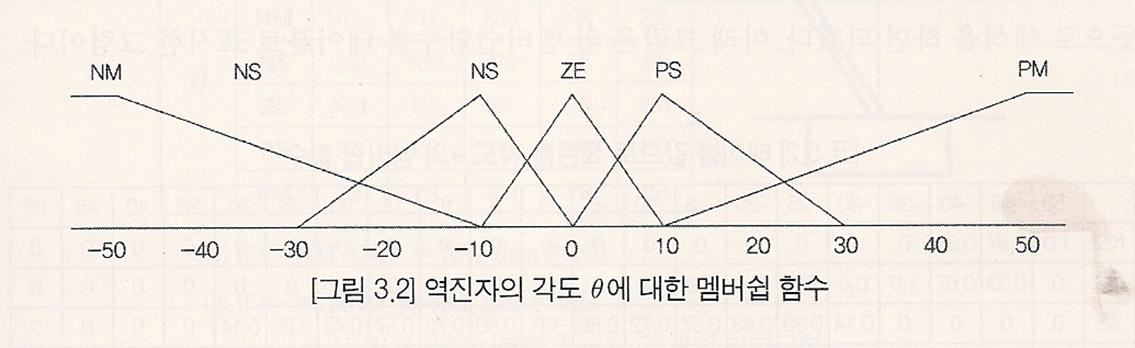
ZE - zero, PS - positive small 이런식

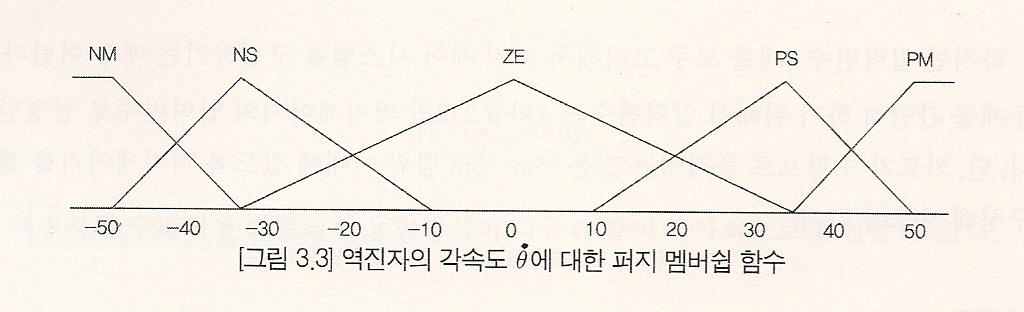
3단계: 퍼지 규칙을 구성하고 도출

전문가의 도움을 받아 퍼지 규칙을 도출한다.

퍼지 규칙을 행렬도 나타내면 편이한 경우가 많다.

2 x 1 시스템(입력2개 출력1개)은 입력 변수의 M X N 행렬로 나타낼 수 있다. 입력 변수의 하나는 가로축 언어값, 다른 입력 변수의 언어값은 세로축을 이룬다.

행과 열이 교차하는 지점에는 출력 변수의 언어값을 놓는다. 3 X 1 시스템은 3차원 행렬(M X N X K)로 표현된다. 이러한 표현 형식을 퍼지 연관 행렬 (FAM)이라고 함

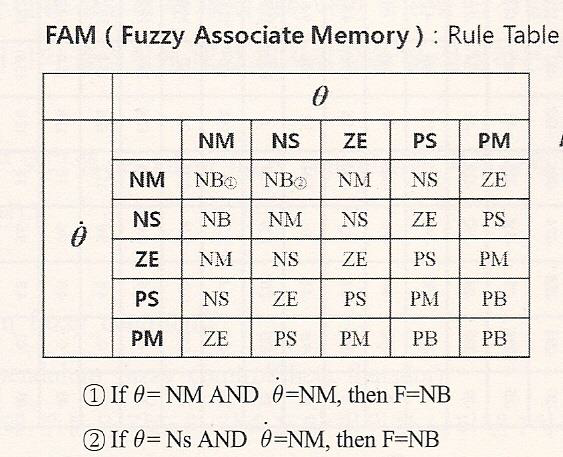
4단계: 퍼지 집합, 퍼지 규칙, 퍼지 추론을 수행하는 절파를 퍼지 시스템에 부호화

퍼지 집합과 퍼지 규칙을 정의하는 다음 단계에서는 이들을 부호화하여 실제 퍼지 전문가 시스템을 구축한다 .

2가지 방법

1. C나 파스칼 같은 프로그래밍 언어를 써서 직접 시스템을 구축

2. MathWorks의 MATLAB Fuzzy Logic Toolbox나 퍼지 시스템 엔지니어링사의 Fuzzy Knowledge Builder Tm같은 퍼지 논리 개발 도구 사용

숙련된 퍼지 시스템 개바자들은 대부분 전자를 선호

하지만 퍼지 전문가 시스템을 빠르게 개발하거나 원형을 만들려면 퍼지 논리 개발 도구가 가장 적당하다.

이들 도구는 보통 퍼시 시스템을 구축하고 테스트 하는 완전한 환경을 제공한다.

5단계 : 시스템을 평가하고 조정

퍼지 시스템 조정은 6가지 순서로 수행가능
1. 모델의 입출력 변수를 재검토하고 필요하면 범위를 재조정
2. 퍼지 집합을 재검토하고, 필요하면 논의 영역에 집합을 추가하거나 퍼지집합의 모양을 바꾼다. 범위가 넓은 퍼지 집합을 쓰면 퍼지 시스템이 세밀하게 작동 안 할수도!
3.** 인접한 집합들이 충분히 겹치게 한다. 얼마나 겹치면 최적인지 결정하는 정확한 방법은 없지만
삼각형-삼각형 or 사다리꼴-삼각형 퍼지집합이 인접할 때는 일반적으로 아랫변의 25~50%가 겹치는것을 권장 **
4. 규칙을 재검토하고, 필요하면 기반 규칙에 새로운 규칙을 추가.
5. 기반 규칙을 검토하고, 헤지 규칙을 작성해서 시스템의 이상한 동작을 잡아낼 가능성이 있는지 알아본다.
6. 규칙 실행 가중치를 바꾼다. 퍼지 논리 대부분은 가중치 배율을 바꿈으로써 규칙의 중요도를 제어 가능

퍼지 전문가 시스템 요약

퍼지 논리

모호함을 설명하는 논리 인간의 감각을 모델링하려 하기 때문에 기계를 좀 더 인간에 가깝고 지능적으로 만듦

얀 루카지위츠가 1920년대에 소개, 맥스 블랙이 1930년대에 심화, 로트피 자데가 1960년대에 재발견,

퍼지 논리는 고전적인 인진 논리의 크리스프 소속성보다 소속된 정도에 바탕을 두고 표현하는 지식에 대한 수학 법칙의 집합 . - 퍼지 논리는 다치논리

퍼지 집합

사람의 키를 작은키, 보통키, 큰키로 나누는 것처럼 경계가 모호(퍼지)한 집합

퍼지 집합을 컴퓨터에서 나타내려면 퍼지집합을 함수로 나태내고 집합의 원소를 소속도에 대응

퍼지 전문가 시스템에서 쓰는 전형적인 소속 함수는 삼각형과 사다리꼴이다.

언어 변수

언어 변수는 막연하거나 모호한 값에 연관된 용어나 개념을 설명하는 데 쓰인다.
이값들은 퍼지집합으로 표현

헤지

헤지는 퍼지 집합의 모양을 바꾸는 퍼지 집합 한정사.
헤지는 매우, 얼마간, 꽤,다소, 조금 같은 부사를 포함

집중 연산은 퍼지 원소의 소속도를 낮춘다.
확장 연산은 퍼지 원소의 소속도를 높인다.

퍼지 집합끼리 상호작용이 가능, 퍼지 집합의 관계를 연산이라고 한다. 주요 연산에는 여집합,포함관계, 교집합, 합집합이 있다.

퍼지 규칙

퍼지 규칙은 인간의 지식을 포착하는데 쓰인다 .
퍼지 규칙은 다음과 같은 형태를 띠는 조건문이다.

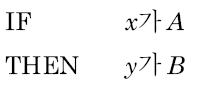
x와 y는 퍼지 집합에 따라 결정된 언어 변수이고 A와 B는 언어값이다.

퍼지 추론

퍼지 추론은 퍼지 집합론은 이용해 주어진 입력을 출력에 대응시키는 과정

4 단계 포함
입력 변수의 퍼지화 -> 규칙 평가 -> 출력으로 나온 규칙의 통합 -> 역퍼지화

맘다니 방법 / 스게노 방법

맘다니 방법은 퍼지 규칙상의 전문 지식을 포착하는 능력 때문에 퍼지 전문가
시스템에서 널리 쓰인다. 그러나 맘다니형 퍼지 추론을 수행하려면 상당한 시간이
걸린다.

퍼지 추론을 효율적으로 계산하기 위해 스게노는 규칙 후건의 소속 함수로서 막대
하나로 된 단일체를 도입했다.

스게노 방법은 최적화나 적응형 기법과 함께 잘 작동한다. 이 특성 때문에 스게노형
추론은 제어, 특히 동적 비선형 시스템에서 매우 매력적이다.

퍼지 전문가 시스템 구축

퍼지 전문가 시스템 구축이란 -> 퍼지 집합과 퍼지 규칙을 정의한 다음, 정해진 요구 조건에 따라 시스템을 평가하고, 조정하는 작업을 반복하는 과정

조정은 퍼지 시스템 구축에서 가장 힘들고 지루 .

이미 정해진 퍼지집합과 퍼지규칙을 정비하는 작업이 포함됨.

퍼지 전문가 시스템은 끝!
MATALB 사용하는것은 안썻다. 따로 보자