사실 텐서 플로우보다 먼저 배웠던 거지만 시험기념 복습하는 김에 작성!
퍼지 논리
퍼지 사고란
인간의 행동은 모호한 정보를 많이 이용한다.
퍼지 논리는 이러한 모호함을 다루기 위한 수리 논리이다.
낱말, 의사 결정, 상식에 관한 인간의 감각을 모델링하려고 하기 때문에 기계를 좀더 인간에 가깝고 지능적으로 만든다.
퍼지 논리는 소속된 정도에 바탕을 두고 표현하는 지식에 대한 수학 법칙의 집합이다. = 다치 논리
불 논리
Boolean Logic - 참과 거짓이 확실하게 구문됨
불논리의 불합리 - 키가 180cm 이상이면 큰키 아니면 작은키라 가정
179 cm인키는 정말 작은것일까?
퍼지논리는 따라서 경계가 불분명한 척도를 나타낼때 사용된다.
고전적인 불 논리처럼 소속을 분명히 하는 것이 아니라. 어느 정도 속하는지를 바탕으로 지식을 표현한다. 따라서 - 다치 논리(multi-valued logic)이다.
크리스프 집합
유한한 참조 초집합 또는 논의영역 X상의 크르스프 집합 A는 A에 대한 특성 함수 fA(x)를 써서 정의한다. a는 조그만 A이다.
fA(x) : X -> {0,1}
영역 X의 특정원소 x가 있을때 특성함수 fA(x)는 x가 A의 원소면 1이고, x가 A의 원소가 아니면 0이다.
퍼지 집합
퍼지 집합은 사람의 키를 작은 키, 보통키, 큰 키로 나누는 것처럼 경계가 모호(퍼지)한 집합이다.
논의 영역 X상의 퍼지집합 A는 함수 μA(x)를 써서 정의한다.
이함수를 집합 A에 대한 소속함수(membership function)라 함 소속함수는 x가 집합 A에 속하는 정도를 나타댐


키가 큰 남자에 대한 크리스프 집합과 퍼지집합
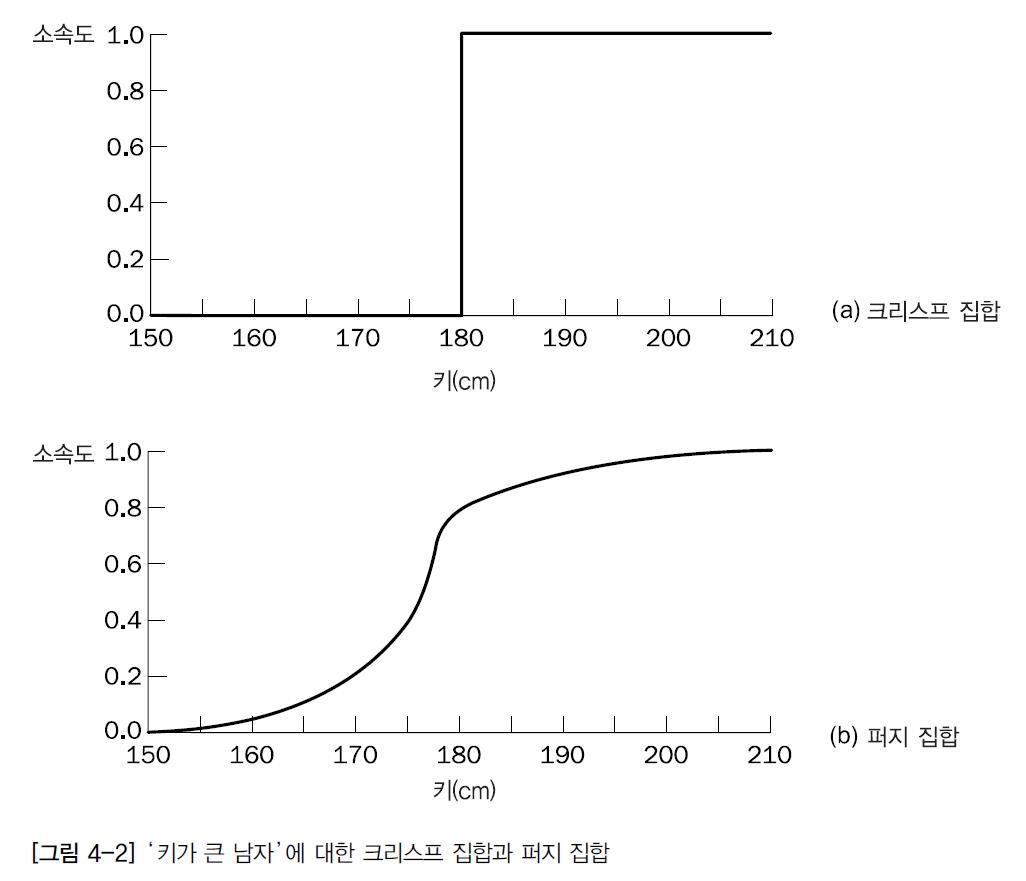
가로축은 논의 영역 / 세로축은 퍼지집합에 대한 소속값을 나타낸다.
키가 작은 남자 , 키가 보통인 남자, 키가 큰 남자에 대한 크리스프집합과 퍼지 집합
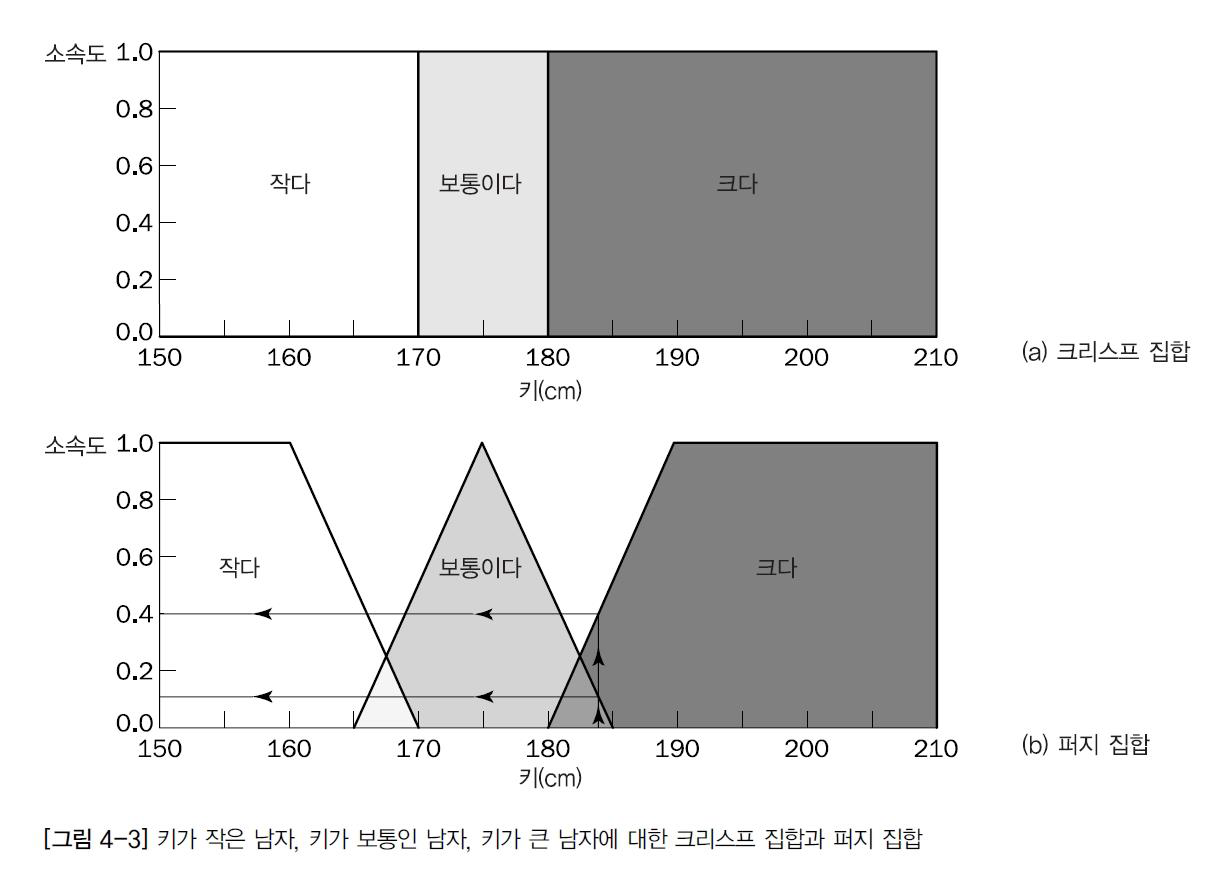
연속적인 퍼지 집합을 컴퓨터로 나타내려면 이를 함수로 나타내고 집합의 원소를 소속도에 대응 시켜야 한다.
이때 쓰는 전형적인 함수로는 시그모이드(sigmoid), 가우스(gaussian), 파이(pi) 함수가 있다.
위의 함수들은 퍼지 집합의 실수 데이터를 나타낼 수 있으나 계산 시간을 증가시킨다. 그렇기 때문에 실제 응용에서는 대부부느 선형 적합 함수를 사용한다.

이런식으로 표현!! 0.5 값은 안 넣어줘도 된다.
언어 변수
퍼지 집합론의 뿌리에는 언어 변수라는 개념에 있다.
언어 변수는 퍼지변수(fuzzy variable)이다.
퍼지 전문가 시스템에서는 언어 변수를 퍼지 규칙에 사용한다.

언어 변수 하나에 할당되는 값의 범위는 해당 변수에 대한 논의 영역을 나타낸다.
언어 변수 속도에 대한 논의 영역은 0~220km/h까지고 매우느리다 ~ 매우 빠르다 같은 퍼지 부분집합을 포함할 수 있다.
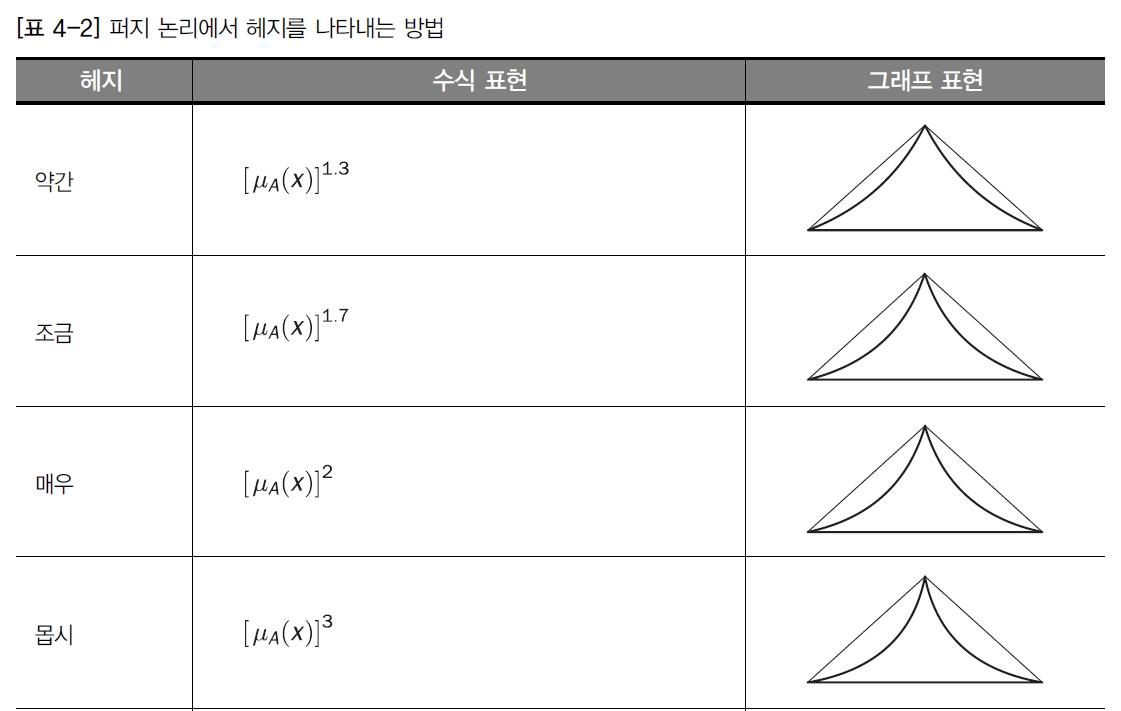
헤지(hedge)
헤지는 퍼지 집합의 모양을 바꾸는 퍼지 집합 한정사이다.
ex) 매우,얼마간, 꽤, 다소, 조금 등등
헤지는 연산자처럼 작동한다.
집중 연산
퍼지 원소의 소속도를 낮춘다. '매우'는 집중(concentration) 연산을 수행하고 새로운 집합을 만든다.
ex) 키가큰 남자 집합에서 헤지 '매우'는 매우 키가큰 남자 라는 부분집합을 만든다.
헤지 '매우'의 퍼지 집합
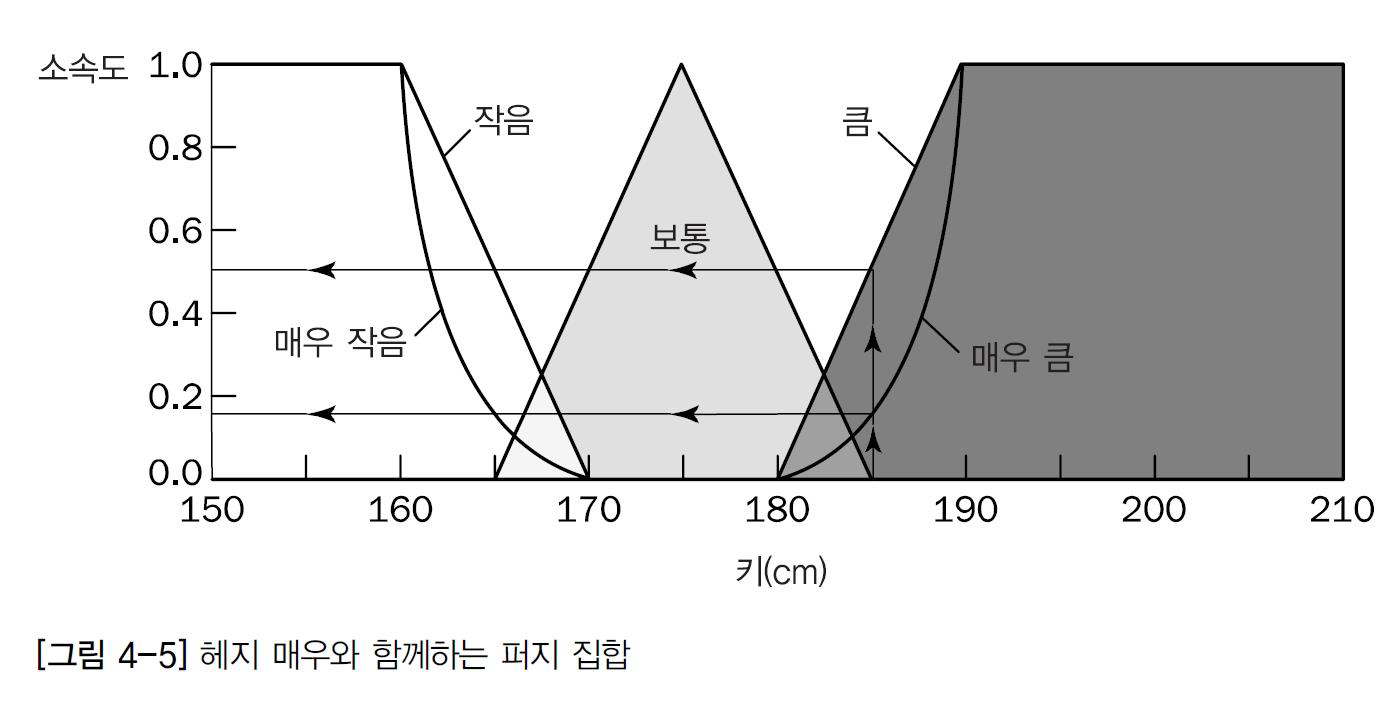
확장 연산
퍼지원소의 소속도를 높인다. 헤지 '다소'는 확장연산을 수행.
다소 키가 큰 남자의 집합 범위 > 키가 큰 남자의 집합의 범위
강화 연산
강화연산은 소속도가 0.5보다 크면 소속도를 더 높이고 0.5보다 작으면 더 낮춘다
ex) 확실히 키 큰사람
실제 응용에서 자주 사용되는 헤지
매우(very) -집중 연산
이 연산은 수학의 제곱 연산이다.

어떤 사람이 키가큰 남자 집합에 0.86만큼 속하면 매우 키카큰 남자 집합에는 0.86의 제곱값인 0.7396만큼만 속한다.
몹시(extremely) - 집중 연산
매우와 비슷한 요화 이 연산은 μA(x)를 세제곱 한것이다.

어떤 사람이 키가큰 남자 집합에 0.86만큼 속하면 몹시 키가 큰 남자에는 이의 세제곱 0.6361만큼 속한다.
매우매우(very very) - 집중 연산
집중 연산을 단순히 확장한 것이다. 집중 연산을 제곱한 것
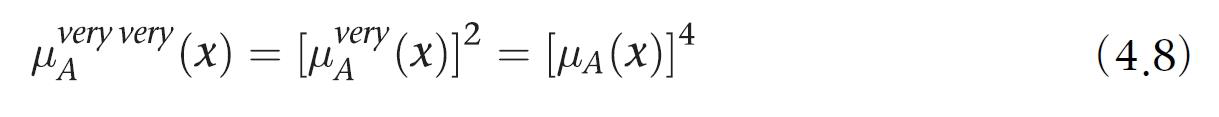
다소(more or less) - 확장 연산
집합을 확장함으로써 퍼지원소들의 소속도를 높인다.

키가큰 남자의 집합에 0.86만큼 속하면 다소 키가큰 남자 집합에는 0.9274만큼 속한다.
확실히(Indeed) - 강화 연산
모든 문장의 의미를 강화한다. 소속도가 0.5 이상이면 소속도를 더 높이고, 0.5보다 낮은 경우에는 더 낮춘다.
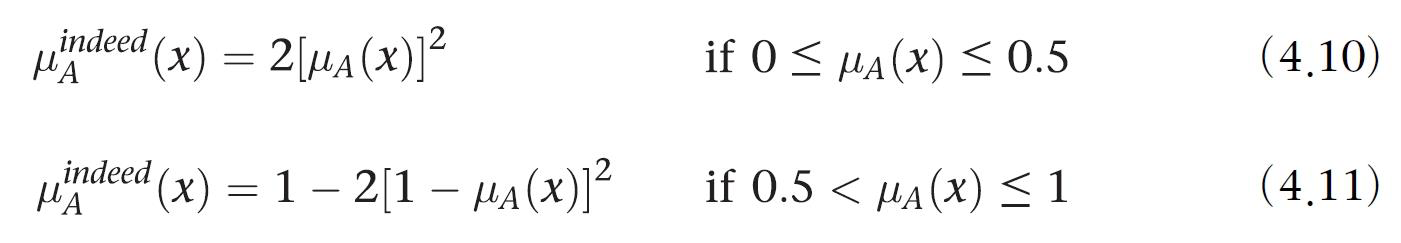
만약 어떤 남자가 키가 큰 남자집합에 0.86만큼 속하면 확실히 키가큰 남자 집합에는 0.9608만큼 속한다.
반대로 키가 큰 남자 집합에 0.24만큼 속하면 확실히 키가 큰 남자 집합에는 0.1152 만큼 속한다.
수업때는 매우, 다소, 확실히 에대해서만 다뤘다.

퍼지 집합 연산
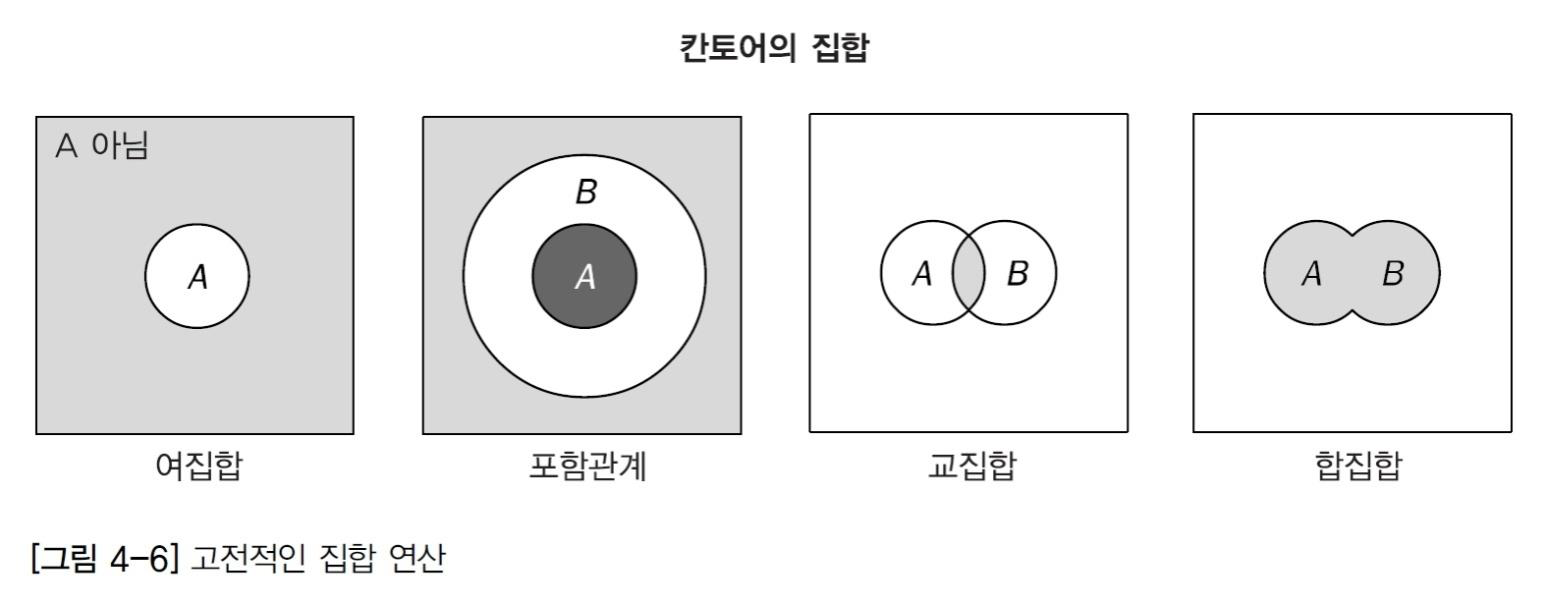
고전적인 집합 연산
게오르그 칸토어가 발전시킨 고전 집합론은 크리스프 집합들이 어떻게 상호작용하는지를 설명
이러한 상호작용을 연산이라고 한다.
여집합, 포합관게, 교집합, 합집합 - 네가지가 있다.
여집합 (complement)
크리스프 집합 - 어떤 원소가 그 집합에 속하지 않을까?
퍼지 집합 - 원소들이 그 집합에 얼마만큼 속하지 않을까?
집합의 여집합은 해당 집합의 반대를 의미한다.
ex) 키가 큰 남자 집합의 여집합은 키가 크지 않은 남자집합
A가 퍼지 집합이라면 여집합 ㄱA는

이와같이 논의 영역에서 빼면 된다.

포함관계 (containment)
크리스프 집합 - 어떤 집합이 다른 집합에 속할까?
퍼지 집합 - 어느 집합이 다른 집합들에 속할까?
포함되는 쪽을 부분 집합(subset)이라 한다.
'매우 키가큰 남자'는 '키가 큰 남자'의 부분집합이다.
크리스프 집합에서는 부분집합의 모든 원소는 초집합 에 완전히 속하고 소속값은 1이된다.
퍼지 부분 집합 원소들의 부분 집합에 대한 소속값은 초집합에 대한 소속값보다 작다.
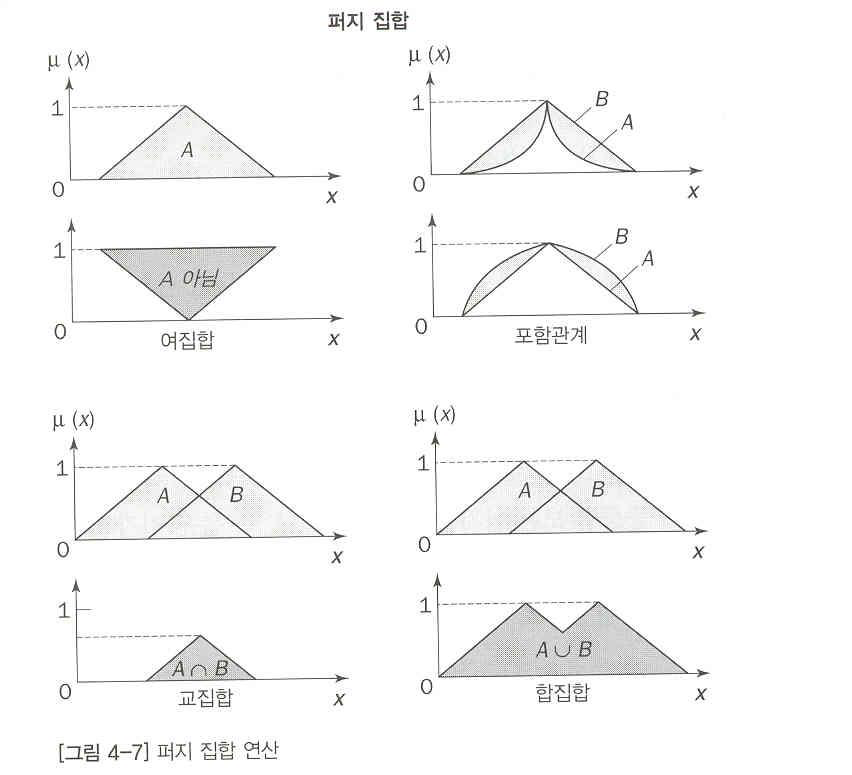
교집합 (intersection)
크리스프 집합: 어느 원소가 두 집합 모두에 속할까?
퍼지 집합: 원소가 두 집합 모두에 얼마만큼 속할까?
퍼지 집합에서는 한 원소가 두 집합에 서로 다른 정도로 부분적으로 속할 수 있다.
각 원소의 퍼지 교집합에 대한 소속값은 두 집합에 대한 소속 값 중 낮은 값이 된다. ( 두개중 낮은 ㄱ밧을 채택 )
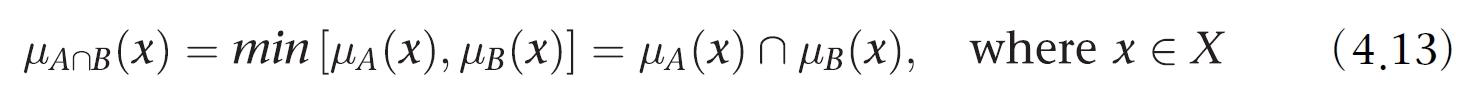

둘중 작은 값을 취한다.
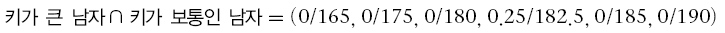
두 집합의 교집합은 뒤와같다.
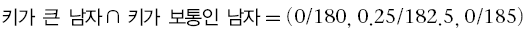
정리하면 위와 같다.
합집합 (union)
크리스프 집합 : 원소가 두 집합 어느쪽이든 속할까?
퍼지 집합: 원소가 두 집합 어느 쪽이든 얼마만큼 속할까?
합집합은 두 집합에 속하는 모든 원소들로 이루어짐
교집합의 반대 : 각 원소의 합집합에 대한 소속 값은 두집합에 대한 소속 값중 높은 값
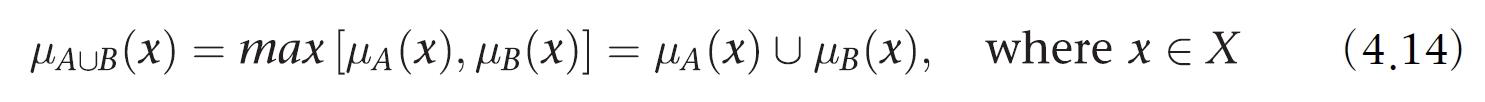
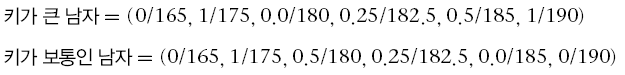
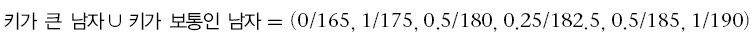
퍼지 집합에서 자주 쓰이는 연산
교환 법칙
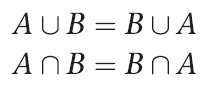
결합법칙
등등 있지만 생략
퍼지 규칙
인간의 지식을 퍼지 규칙으로 표현할 수 있음.

퍼지 규칙은 다음과 같이 형태로 된 조건문으로 정의할 수 있다
x와 y는 언어변수. A와 B는 각각 논의 영역 X와 Y의 퍼지 집합에서 결정된 언어값이다.
고전적인 If-then 규칙
규칙 1
if 속도 >100
then 정지 거리는 길다
규칙 2
if 속도 <40
then 정지 거리는 짧다.
언어 변수 정지거리는 '길다' or '짧다' 두가지 값중 하나만 취할 수 있다. - 흑백이 뚜렷
퍼지 형식
언어 변수 속도는 0~220km/h 범위에 존재
이 범위는 '느리다', '보통이다','빠르다' 같은 퍼지 집합포함
정지거리의 논의 영역은 0~300m 사이에 있을수 있고 '짧다', '보통''길다'같은 퍼지 집합 포함 가능
따라서 퍼지 규칙은 퍼지 집합과 연관되어 있다.
퍼지 추론
퍼지 규칙을 이용한 추론 과정
일반적으로 퍼지 전문가 시스템은 다수의 퍼지 규칙으로 구성 됨
이 규칙들은 전문 지식을 기술하고 서로 영향을 준다.
각 규칙의 출력은 퍼지 집합이다.
그러나 일반적으로 전문가 시스템의 출력을 나타내는 숫자 하나를 필요로 한다
퍼지 추론과정의 4단계
입력 변수의 퍼지화 -> 규칙 평가 -> 출력으로 나온 규칙의 통합 -> 역퍼지화
퍼지 추론 방법
맘다니형 추론
스게노형 추론
맘다니형 추론(Mamdani method)
가장 흔히 쓰이는 퍼지 추론 기법
1975년에 맘다니 교수가 만든것
입력 변수의 퍼지화 -> 규칙 평가 -> 출력으로 나온 규칙의 통합 -> 역퍼지화
ex) 


x,y,z는 언어 변수
A1, A2,A3는 논의 영역 X상의 퍼지 집합에서 정해지는 언어 값.
B1, B2 논의영역 Y상의 퍼지집합에서 정해지는 언어 값.
C1, C2, C3는 논의 영역 Z상의 퍼지 집합에서 정해지는 언어 값.
맘다니형 퍼지 추론의 기본 구조
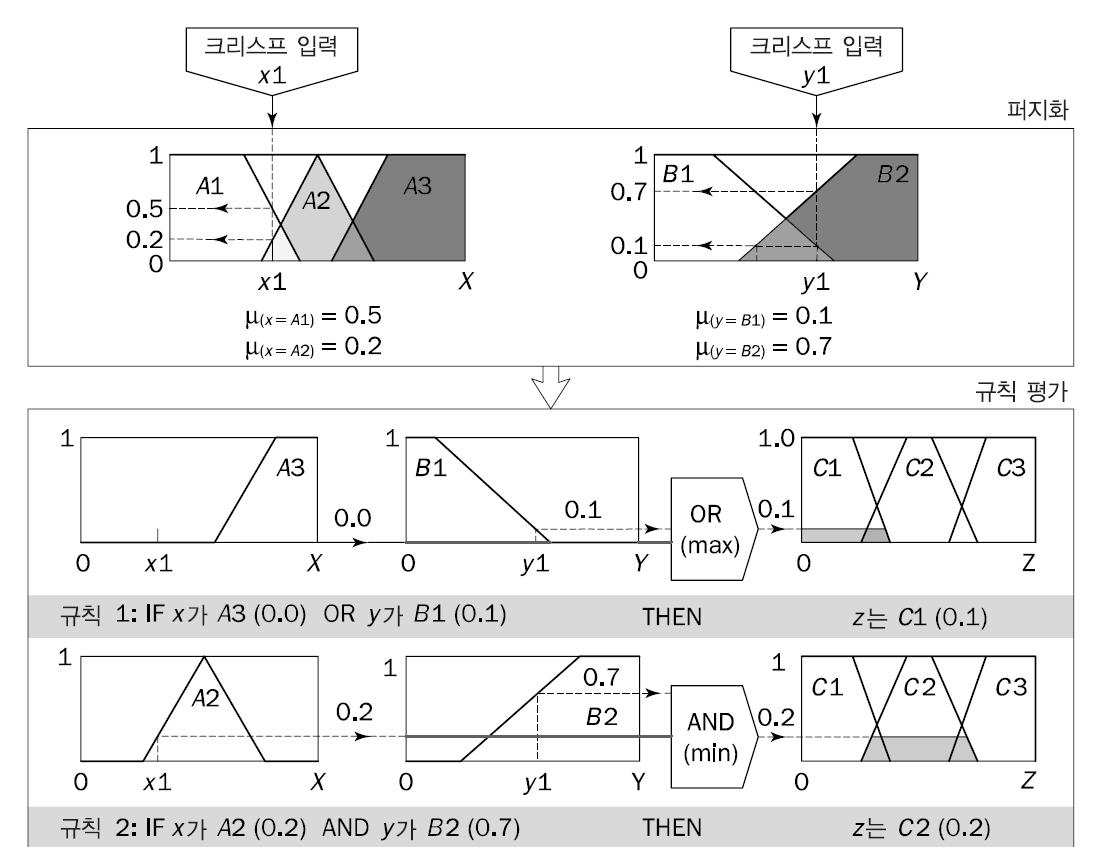
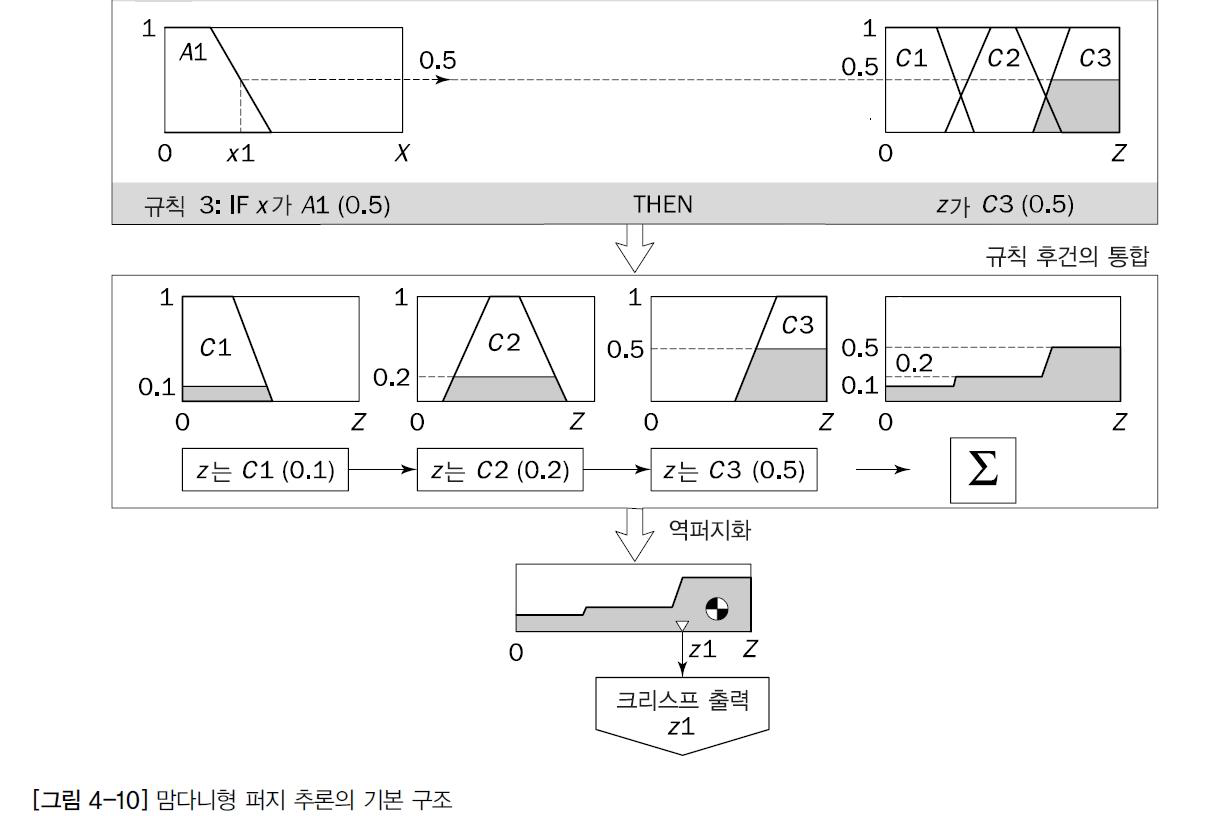
1단계: 퍼지화
첫 단계인 퍼지화에서는 크리스프 입력 x1과 y1(자금,인력)을 받고 적합한 퍼지 집합 각각에 어느정도를 속할지를 결정
크리스프 입력
언제나 논의 영역으로 한정된 수치값.
x1, y1은 논의 영역 X와 Y로 한정된다.
크리스프 입력 x1(전문가가35%로 평가한 프로젝트 자금)은 소속 함수 A1과 A2
(부족하다와 한계 수익점에 있다)에 각각 0.5와 0.2만큼 대응한다.
그리고 크리스프 입력 y1(전문가가60%로 평가한 프로젝트 인력)은 소속 함수 B1과
B2(적다와 많다)에 각각 0.1과 0.7만큼 대응한다
2단계: 규칙 평가(rule evaluation)
규칙 평가 단계에서는 퍼지 입력 μ(x=A1) = 0.5, μ(x=A2) = 0.2, μ(x=B1) = 0.1,μ(x=B2) =
0.7을 받아 퍼지 규칙의 전건에 적용한다
주어진 퍼지 규칙에 전건이 여러개 있다면 AND 나 OR를 사용하여 전건의 평가 결과를 나타내는 숫자 하나를 얻는다. 이 숫자를 후건의 소속 함수에 적용
규칙 전건의 논리합을 평가하려면 OR퍼지 연산은 사용한다. 일반적으로 퍼지 전문가 시스템은 고전적인 합집합을 사용
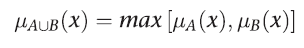
논리합의 평가 밥법으로는 max대신 확률적 OR인 probor를 사용할 수 있다.
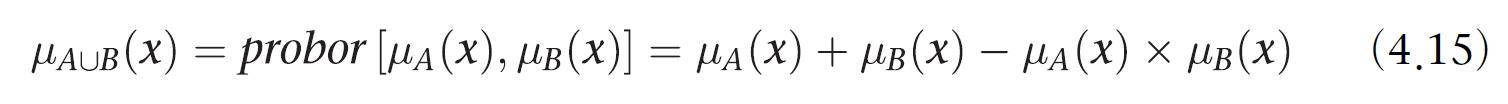
규칙 전건의 논리곱을 평가하려면 AND 연산인 교집합을 사용(가장작은걸 취함)
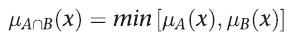
논리곱의 평가 방식으로 min대신 곱인 prod를 사용할 수 있다
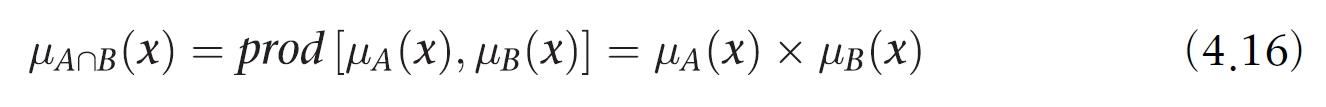
전건의 평가 결과를 후건의 소속함수에 적용할 수 있다. 후건의 소속 함수는 규칙 전건의 진리값 수준으로 클리핑 되거나 스케일링 된다.
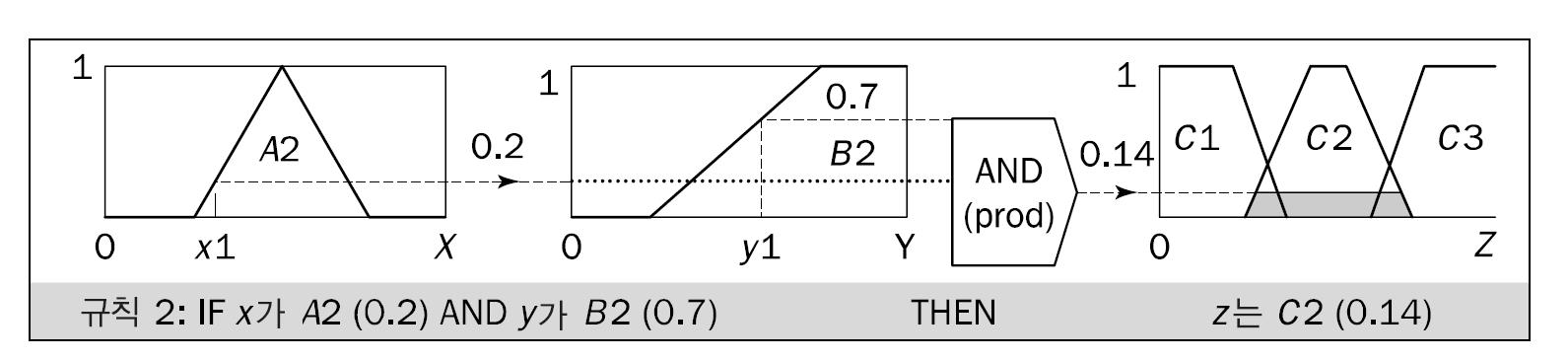
클리핑과 스케일링
후건의 소속 함수를 전건의 진리값 수준에서 자르는 방법을 클리핑 or 상관 최소값
소속 함수의 상단이 잘리기 때문에 클리핑된 퍼지 집합은 정보를 어느 정도 잃는다.
하지만 클리핑은 덜 복잡하고 계산이 빠르며 역퍼지화하기 쉬운 출력층을 만들어서 많이 쓰인다.
규칙 후건에 대한 소속 함수의 모든 소속도에 규칙 적건의 진리값을 곱하여 조정하는 방식을 스케일링이라고 한다.
클리핑을 더 많이 사용하지만 스케일링 즉 상관 곱이 퍼지 집합의 원형을 더 잘 보존, 정보손실 적다. 퍼지 전문가 시스템에서 매우 유용
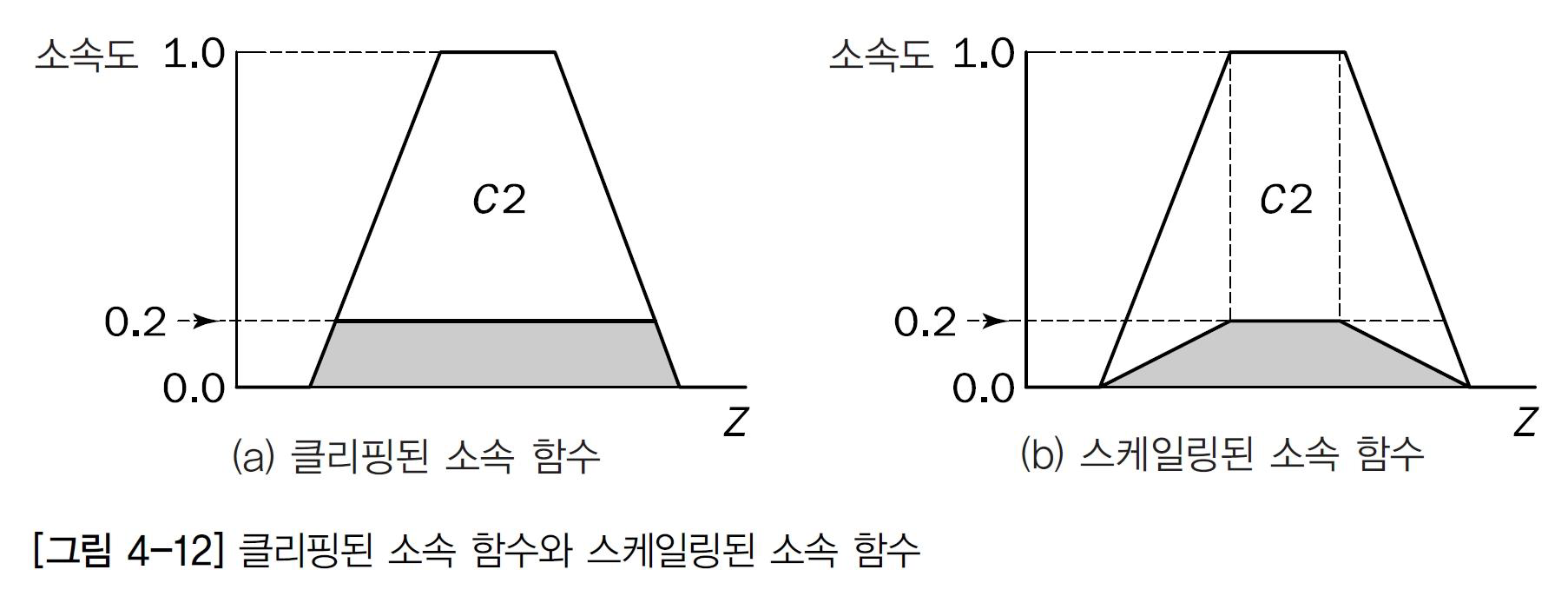
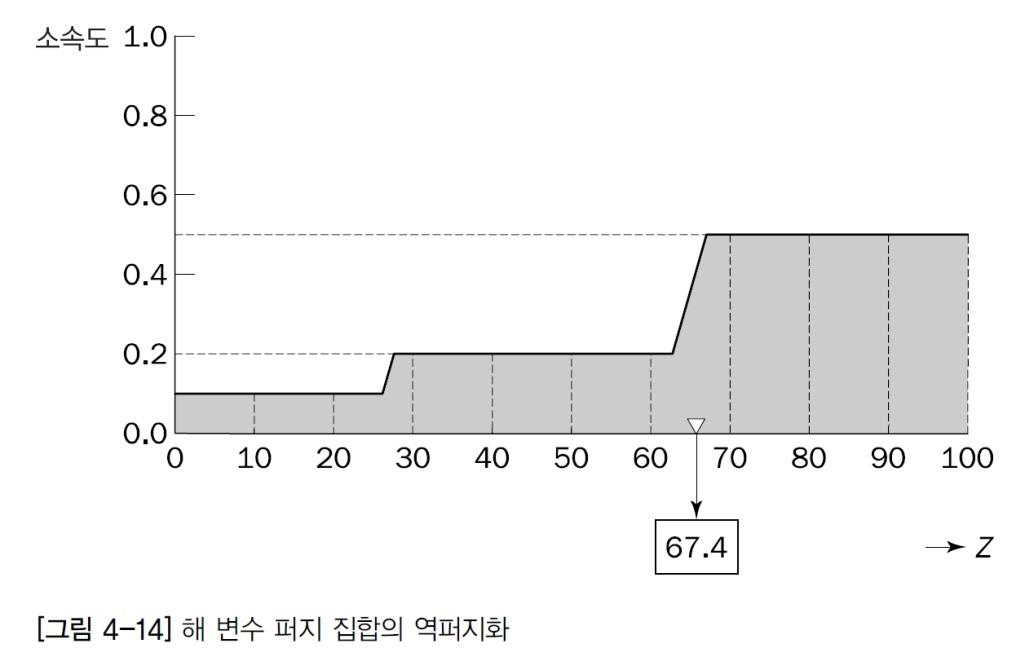
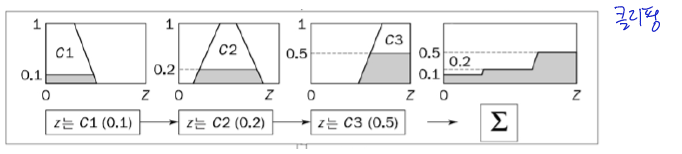
3단계 - 출력으로 나온 규칙을 통함
통합은 모든 규칙의 출력을 단일화 하는 과정이다.
앞 단계에서 클리핑되거나 스케일링된 모든 규칙 후건의 소속 함수를 펒 집합 하나로 결합한다.
따라서 통합 과정의 입력은 클리핑되거나 스케일링된 후건 소속 함수의 목록 / 출력은 출력 변수 각각에 대한 단일 퍼지 집합.
각각의 규칙의 출력이 어떻게 모든 출력에 대해 단일 퍼지 집합으로 통합되는지 보여줌
4단계 : 역퍼지화
퍼지 추론 과정의 마지막 단계는 역퍼지화(defuzzification)다. 입력은 통합된 출력 퍼지 집합이고 출력은 하나다.
퍼지 시스템의 최종 출력은 분명한 숫자여야 한다.
무게 중심법
가장 많이사용되는 역퍼지와 방법
수직선이 통합된 집합을 무게가 같은 두 부분으로 가르는 지점
지점의 값을 최종 결과로 취한다.
수학적으로 무게 중심(COG, centre of gravity)를 다음과 같이 나타낸다.
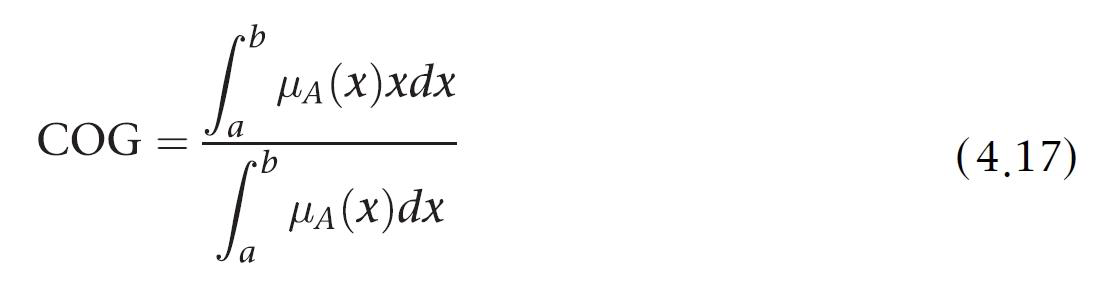
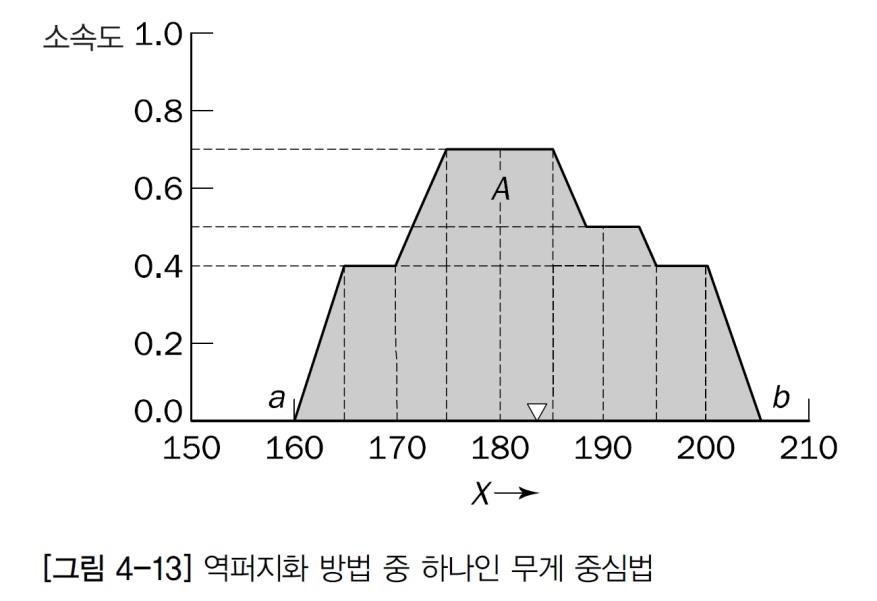
무게 중심은 통합된 출력 소속 함수에 있는 점들의 연속체에 대해 계산된다. but 실제로는 점들의 표본을 추출하여 계산해서 합리적인 추정치를 얻는다.
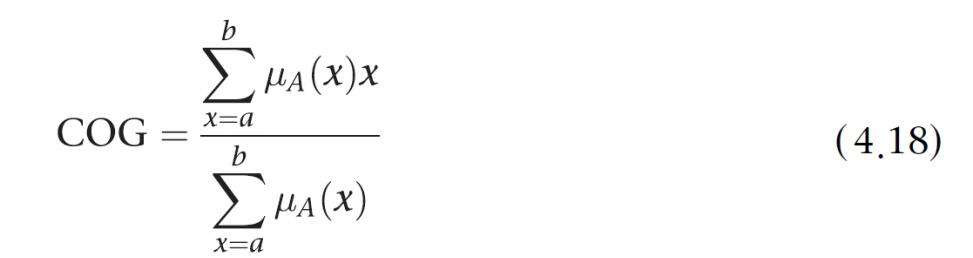
약식으로 추정치를 구하는 방법( 구간을 나눠서 계산한다)

스게노형 추론은 다음 글부터 !!

안녕하세요 좋은 글 감사합니다. 제가 이해력이 부족해서 질문드립니다.
헤지(hedge)에 관한 질문인데요 글에 예시에는 키를 기준으로 (작다, 보통, 크다)
총 가지의 퍼지집합을 정하고 헤지를 통해 총 5단계로 확장하신거 같은데
그럼 처음부터 5단계로 값의 범위를 정해놨을 경우 헤지는 사용할 필요가 없는걸까요?
(매우작다 x<165)
(작다 160<x<170)
(보통 165<x<175)
(크다 170<x<180)
(매우크다 175<x<185)
다시 한 번 좋은 글 감사합니다.