기본적으로 우리는 십진수를 사용하고 있다.

예를들어서 150이라는 숫자를 보면

$1 * 10^2 + 5 * 10^1 + 0*10^0$ 이다.

이것이 십진법의 가장 큰 특징이다. 자리수가 늘어날 때 마다 10씩 곱해진다는 것이다.

또한 십진법의 큰 특징 중 하나는 바로 0~9 까지 10개의 숫자를 활용한다는 것이다.

즉 특징은 다음과 같이 말할 수 있다.

• 자리수가 늘어날때 마다 10씩 곱해진다
• 10가지(0~9)의 숫자를 사용한다

이진수

컴퓨터는 0과 1 두가지만 인식할 수 있다. 그래서 십진법의 이러한 아이디어를 이진수에 접목시켜보자

2진법 0과 1 두개의 숫자만 사용하고 자리수가 늘어날 때 마다 2씩 곱해진다.

예를 들어서 6은

$1\times2^2+1\times2^1+0\times2^0=110_2$

나타낼 수 있다. 앞서 십진법과 규칙이 동일하다.

한자리씩 늘어날 때 마다 2씩 곱해지고 1과 0 2가지의 숫자만 사용했다.

$49= 32 + 16 + 1 = 1 \times 2^5 + 1 \times 2^4 + 0 \times 2^3 + 0 \times 2^2 + 0\times 2^1 + 1 \times 2^0 = 110001_2$

십진수를 이진수로 표현하는 것은 복잡해 보이지만 사실 간단하게 2로 계속 나누면 쉽게 표현할 수 있다

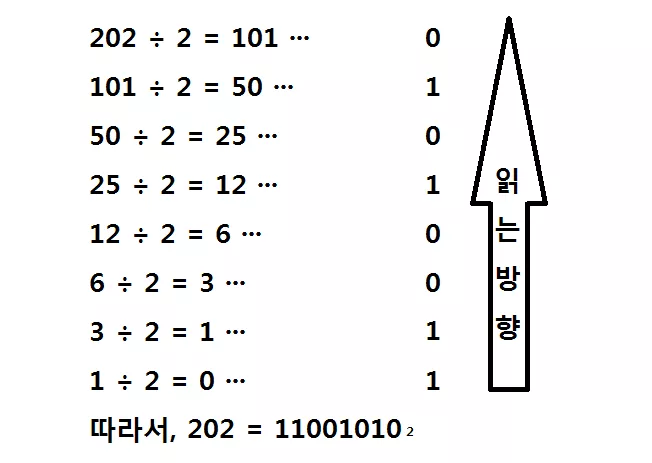
하지만 이진법의 단점은 너무 길다는 것이다.

1024의 경우 십진법은 4자리로 표현할 수 있지만 이진법으로 10000000 8자리로 표현해야 한다.

그렇기 때문에 사람의 입장에서 읽기 번거롭기 때문에 프로그래머들은 보통 16진법을 사용하고 있다.

16진법

16진법에서 주목해야 하는 것은 16가지의 숫자가 필요하다는 것이다. 그러나 우리가 아는 숫자는 0부터 9까지 10개이므로 10부터 15까지 알파벳을 사용한다.

0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

16진법도 2진법과의 마찬가지 논리로 적용시켜보면 다음과 같다

$123=7×16+11=0x7B$

0x 는 16진수라는 것을 나타내고 B는 11을 말한다.

$16782=4×163+1×162+8×161+14×160=0x418E$

16진수를 10진수로 바꾸거나 10진수를 16진수로 바꾸는 것은 앞서 2진법에서 했던 방법과 똑같다.

이는 단순하지만 지저분하고 매우 복잡하다.

하지만 16진수를 2진수로, 2진수를 16진수로 바꾸는 것은 매우 간단하다.

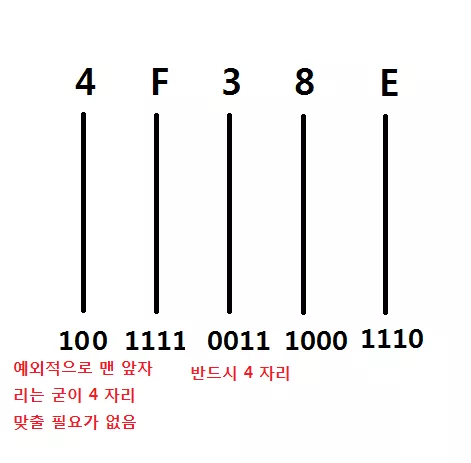
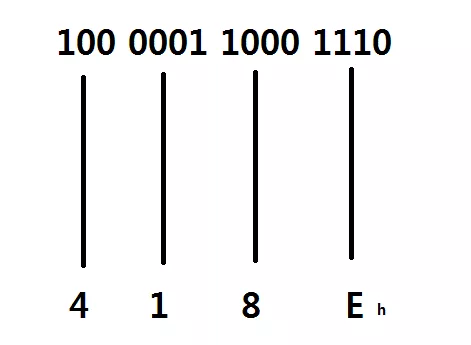
위와 같이 0x4F38E 를 2 진수로 변환하면 1001111001110001110 가 된다.

마찬가지로 2진수를 16진수로 바꾸는 것도 간단하다.