코딩테스트 특강에서 들은 내용을 정리해보도록 하겠습니다.
코딩테스트
정의
자료구조와 알고리즘을 결합한 문제 해결 능력을 보는 테스트이다.
준비 사항
- 코테를 보는 회사와 회사 유형을 정리하기
- 사용가능한 라이브러리 확인
- 언어 선택
- 코드 스니펫
- 감독관이 없는 경우, 스니펫을 활용
- 유용한 라이브러리 정리
- 예외 처리
- 속도 개선
- 클래스, 슬라이싱, for문 대신 리스트 컴프리헨션 등
- ChatGPT, Copilot 활용(가능하다면)
문제 유형과 출제 방식
시간과 문제 수는 다양하며 전부 다 맞춰야 통과하지는 않는다.
- 주로 출제되는 알고리즘
- 요구사항 구현(33%)
- 그리디(20%)
- 너비우선탐색, 깊이우선탐색(20%)
- 정렬(8%)
- 다이나믹 프로그래밍, 최단 경로, 이진 탐색 등
워밍업 문제
- 카운팅
# 1부터 10,000까지 8이라는 숫자가 총 몇번 나오는가?
# 8이 포함되어 있는 숫자의 갯수를 카운팅 하는 것이 아니라 8이라는 숫자를 모두 카운팅 해야 한다. (※ 예를들어 8808은 3, 8888은 4로 카운팅 해야 함)
str(list(range(1, 10001))).count('8')리스트를 문자로 바꿀 수 있으므로 문자로 바꿔 문자열 메서드인 count를 사용한다.
- 최대, 최소 기본
# 최대
l = [10, 20, 11, 15, 17, 21, 13]
result = -float('inf')
for i in l:
if i > result: # 최소는 연산자 방향이 반대
result = i
result- 최대, 최소 응용
1차원의 점들이 주어졌을 때, 그 중 가장 거리가 짧은 것의 쌍을 출력하는 함수를 작성하시오. (단 점들의 배열은 모두 정렬되어있다고 가정한다.)
예를들어 S = [1, 3, 4, 8, 13, 17, 20] 이 주어졌다면, 결과값은 (3, 4)가 될 것이다.
list(zip(s, s[1:]))
sorted(zip(s, s[1:]), key=lambda x: x[1] - x[0])
sorted(zip(s, s[1:]), key=lambda x: x[1] - x[0])[0]max와 min을 사용할 수도 있지만 그러한 함수 없이 구해야할 경우도 있다. 사용하지 않고 구현하였다.
zip 함수를 사용한 정렬을 사용한다면 파이썬답게 쉽게 구현가능하다.
가장 거리가 짧은 쌍 및 긴 쌍을 구하는 것도 간단하다. 가장 뒤의 원소를 구하면 된다.
짤막 지식
-10 // 3 # -4// 는 내림이다.
-float('inf') < -100000000000000000000000 # True
float('-inf') < -100000000000000000000000 # True
float('inf') > 100000000000000000000000 # True파이썬 inf 무한대는 수학의 무한대가 아니다.
스택과 큐
수강생 중 스택을 프링글스 통과 큐를 자동세차장이라고 한 분이 있었는데 꽤 괜찮은 표현인 것 같다.
깊스너큐 라는 말이 있다. 깊이 우선 탐색은 스택으로 풀고, 너비 우선 탐색은 큐로 푼다는 뜻이다.
스택은 일반적으로 다음과 같은 리스트를 생각하면 된다.
# 스택
s = []
# 값 삽입
s.append(10)
s.append(20)
s.append(30)
# 값 꺼냄
s.pop()뒤에서 작업이 이루어진다.
큐는 일반적으로 값을 뒤에 추가했으면 앞에서 꺼내고, 앞에 추가했으면 뒤에서 꺼내는 특징이 있다.
# 보통의 queue
# s = <- [] <-
s = []
# 값 삽입
s.append(10)
s.append(20)
s.append(30)
# 값 꺼냄
s.pop(0)
# 내맘대로 queue
# s = -> [] ->
s = []
# 값 삽입
s.insert(0, 10)
s.insert(0, 20)
s.insert(0, 30)
# 값 꺼냄
s.pop()스택 큐 문제
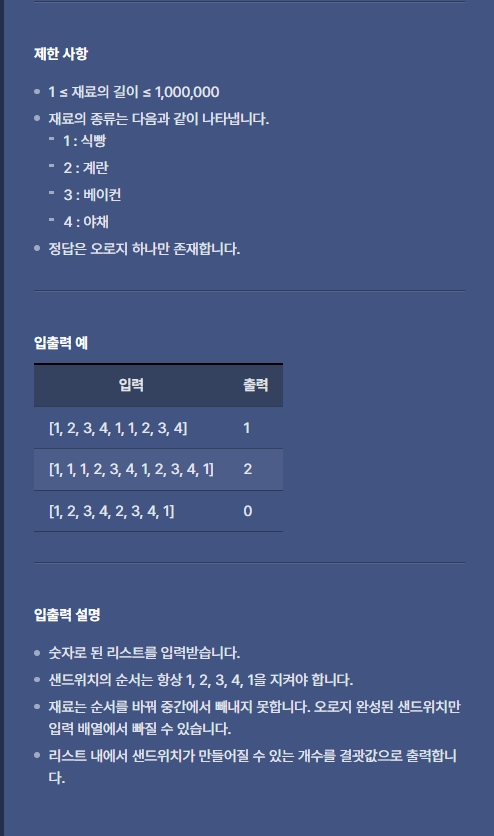
[1, 2, 3, 4, 1] 으로 원소가 배치되어 있을때 카운트가 하나 증가하는 문제이다.
data = [1, 1, 1, 2, 3, 4, 1, 2, 3, 4, 1]
stack = []
count = 0
for i in data:
stack.append(i)
if stack[-5:] == [1, 2, 3, 4 ,1]:
for _ in range(5):
stack.pop()
count+= 1
print(count)
stack == [1]
stack == [1, 1]
stack == [1, 1, 1]
stack == [1, 1, 1, 2]
stack == [1, 1, 1, 2, 3]
stack == [1, 1, 1, 2, 3, 4]
stack == [1, 1, 1, 2, 3, 4, 1] # 여기서 마지막 5개가 [1, 2, 3, 4, 1]이 매칭이 됩니다!
# => [1, 1]
stack == [1, 1, 2]
stack == [1, 1, 2, 3]
stack == [1, 1, 2, 3, 4]
stack == [1, 1, 2, 3, 4, 1] # 여기서 마지막 5개가 [1, 2, 3, 4, 1]이 매칭이 됩니다!
# => [1]- 풀이 순서
- 데이터, 스택(리스트), 카운트 변수를 정의한다.
- 반복문을 돌면서 스택에 원소를 추가한다.
- 스택의 마지막 5개의 원소가 [1, 2, 3, 4, 1]과 같으면 카운트를 증가시키고 그 5개의 원소를 지운다.
- 반복문이 종료될 때까지 반복하며 카운트를 반환한다.
연결리스트
메모리 효율을 위해 사용된다. 리스트의 원소들이 순서대로 쫙 있는 것이 아닌, 떨어져 있으며 next로 이어져 있다.

- 간단한 연결리스트 구성
연결리스트 = {
'head' : {
'value': 22,
'next': {
'value' : 2,
'next' : {
'value' : 90,
'next' : {
'value' : 77,
'next' : None
}
}
}
}
}head는 처음 리스트 조각(부분?)을 말하고 value는 그 부분에 저장된 값, next는 연결될 다음 리스트를 의미한다.
연결리스트['head']['next']['next'] # {'value': 90, 'next': {'value': 77, 'next': None}}-
문제
- head -> [90, next] -> [2, next] -> [77, next] -> [35, next] -> [21, next] -> None
- 35를 출력해주세요.
연결리스트 = { 'head': { 'value': 90, 'next': { 'value': 2, 'next': { 'value': 77, 'next': { 'value': 35, 'next': { 'value': 21, 'next': None } } } } } } # 출력문 연결리스트['head']['next']['next']['next']['value'] # 35 -
예시 1
node1 = {
'value': 12,
'next': None
}
node2 = {
'value': 99,
'next': None
}
node3 = {
'value': 37,
'next': None
}
node1['next'] = node2
node2['next'] = node3
node1['next']['next']['value']보통 next로 계속 이어지는 것이 아닌 위처럼 나눠서 선언한 후 연결하는 방식으로 사용한다.
- 예시 2
class Node:
def __init__(self, data):
self.value = data
self.next = None
node1 = Node(90)
node2 = Node(2)
node3 = Node(77)
node4 = Node(35)
node1.next = node2
node2.next = node3
node3.next = node4
node1.next.next.value조금 더 효율적인 연산을 위해 클래스를 사용해서 구현하였다. 딕셔너리는 다양한 메서드들이 있기에 빠른 구현을 위한 방법이다. 특정 원소 1개만 출력하는 예시이다.
- 예시 3
class Node:
def __init__(self, data):
self.value = data
self.next = None
node1 = Node(90)
node2 = Node(2)
node3 = Node(77)
node4 = Node(35)
node1.next = node2
node2.next = node3
node3.next = node4
currentnode = node1
while currentnode:
print(currentnode.value)
currentnode = currentnode.next연결리스트의 모든 원소를 while문으로 전부 출력하는 예시이다. 연결리스트 문제는 위와 같은 구성을 베이스로 잡고 진행한다.
