[day-57] 연결리스트, 트리, 연습문제

Joohyung Park·2024년 3월 27일

[모두연] 오름캠프

목록 보기

93/95

어제에 이어서 연결리스트를 알아보도록 하자.

연결리스트

노드 추가하기

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None


class LinkedList:
    def __init__(self):
        init = Node('init')
        self.head = init
        self.tail = init
        self.count = 0

    def append(self, data):
        new_node = Node(data)
        self.tail.next = new_node
        self.tail = new_node
        self.count += 1

l = LinkedList()
l.append(10)
l.append(20)
l.append(30)
l.append(40)
l.append(50)
l # <__main__.LinkedList at 0x79d6c04c2650>

LinkedList 함수에서 __init__ 메서드로 초기 노드, head(맨앞), tail(맨뒤), count 변수를 정의하였다.

원소를 추가하는 append 함수를 정의하고 , 추가할 노드를 new_node로, 맨뒤에 추가될 예정이므로 현재 리스트의 next를 새로운 노드로 연결한다.

이후, 맨뒤 노드가 변경되었으므로 맨뒤 노드를 재정의 하고 카운트를 증가시킨다.

최종적으로 추가가 되는데, __str__ 메서드와 __repr__ 메서드를 사용하지 않아 위와 같이 나오고 있다.

메서드를 정의하지 않고 뽑고 싶다면 다음과 같이 선언하면 된다.

l.head.next.next.data # 20

전체 원소 출력

currentnode = l.head
while currentnode:
    print(currentnode.data)
    currentnode = currentnode.next

    
# init
# 10
# 20
# 30
# 40
# 50

노드 원하는 위치 추가

insert를 사용하면 원하는 위치에 노드를 삽입하는 코드이다.

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None


class LinkedList:
    def __init__(self):
        init = Node('init')
        self.head = init
        self.tail = init
        self.count = 0

    def __len__(self):
        return self.count

    def __repr__(self):
        s = ''
        currentnode = l.head.next
        while currentnode:
            s += f'{currentnode.data}, '
            currentnode = currentnode.next
        return f'<{s[:-2]}>'

    def __str__(self):
        s = ''
        currentnode = l.head.next
        while currentnode:
            s += f'{currentnode.data}, '
            currentnode = currentnode.next
        return f'<{s[:-2]}>'

    def __iter__(self):
        currentnode = l.head
        while currentnode:
            yield currentnode.data
            currentnode = currentnode.next

    def append(self, data):
        new_node = Node(data)
        self.tail.next = new_node
        self.tail = new_node
        self.count += 1

    def insert(self, index, data):
        currentnode = l.head.next
        new_node = Node(index)
        
        for _ in range(index):
            currentnode = currentnode.next
		
        new_node.next = currentnode.next
        current_node.next = new_node
        self.count += 1
        
l = LinkedList()
l.append(10)
l.append(20)
l.append(30)
l.append(40)
l.append(50)
print(l) # <10, 20, 30, 40, 50>

for i in l:
    print(i)
    
# 10
# 20
# 30
# 40
# 50

len 메서드 : 연결 리스트의 길이를 출력하기 위한 메서드
repr, str 메서드 : 사용자 친화적인 문자열 출력을 위한 메서드
- 현재 노드를 한칸씩 옆으로 옮기면서 출력하기 위함
- <10, 20, 30, 40, 50>
insert 메서드 : 노드를 원하는 위치에 삽입하는 메서드
- 새로운 노드 생성
- 끝까지 반복하며 삽입할 위치 탐색
- 새 노드를 해당 위치에 연결
iter 메서드 : 연결 리스트의 노드를 순회하도록 함
- 현재 노드를 첫 번째 실제 노드로 연결
- 연결리스트 끝에 도달할 때까지 반복
- yield는 값을 반환하고 함수의 상태를 저장하며 다음 값을 요청할 때마다 yield 다음 줄부터 실행
- 현재 노드를 다음 노드로 업데이트

이중 연결 리스트

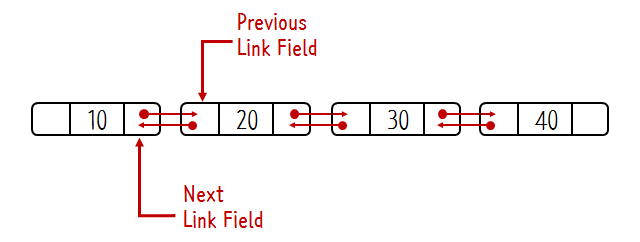
일반 연결 리스트와의 차이점은 앞, 뒤로 이동이 가능하다는 것이다. pre 라는 키워드가 추가되었다.

node1 = {
    'pre': None,
    'data': 12,
    'next': None
}

node2 = {
    'pre': None,
    'data': 99,
    'next': None
}

node3 = {
    'pre': None,
    'data': 37,
    'next': None
}

node1['next'] = node2
node2['pre'] = node1

node2['next'] = node3
node3['pre'] = node2

node1['next']['next']['pre']['next']['pre']['pre']['data'] # 12

위의 경우처럼 앞, 뒤로 이동이 가능한 모습을 보인다.

다양한 문제 풀이

Counter 모듈

from collections import Counter

Counter([1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 3])
# Counter({1: 4, 2: 3, 3: 6})

숫자를 세는데 특화되어 있다.

특정 숫자 등장횟수 세기

from collections import Counter

def solution(array, n):
    value = Counter(array).get(n)
    return 0 if value == None else value

get(n)은 n이라는 키의 값, n이 몇 번 등장하는지를 반환한다.

모듈을 사용하지 않은 풀이

# height보다 큰 수의 등장 횟수 반환 함수
def solution(array, height):
    return len([i for i in array if i > height])


solution([149, 180, 192, 170], 167)

각 자리 숫자의 합

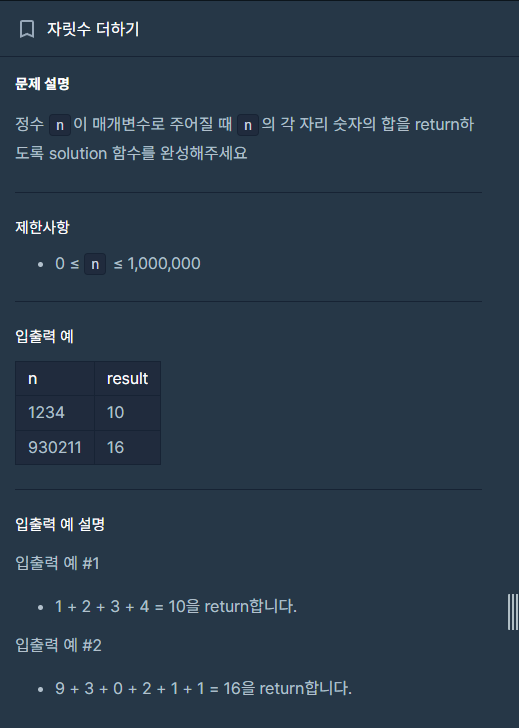
s = 0
for i in str(n):
    if i.isdigit():
        s += int(i)

리스트 1칸씩 밀기

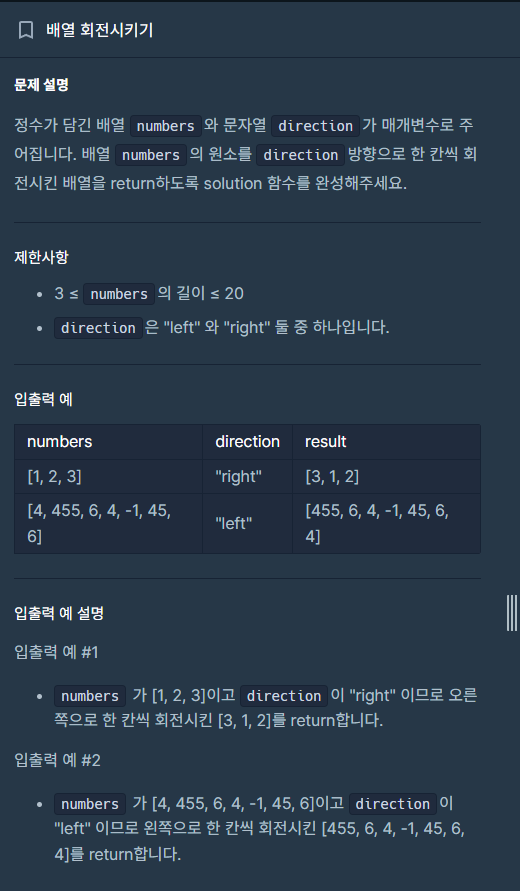
from collections import deque


def solution(numbers, direction):
    numbers = deque(numbers)
    if direction == 'right':
        numbers.rotate(1)
    else:
        numbers.rotate(-1)
    return list(numbers)

deque 모듈의 rotate는 간단하게 리스트의 원소들을 오른쪽, 왼쪽으로 밀 수 있다.

deque 모듈의 메서드로 maxlen 이라는 것도 있는데
이는 deque 길이의 최대값을 정할 수 있다. 최대 값(길이)를 넘어가면 자동으로 가장 먼저 추가된 원소를 1개씩 삭제한다.

모듈을 사용하지 않은 풀이

order = 'right'
numbers = [1, 2, 3]
result = []
if order == 'right':
    result = [numbers[-1]] + numbers[:-1]
else:
    result = numbers[1:] + numbers[0]
result

정규 표현식

숫자끼리 더해서 반환하는 문제

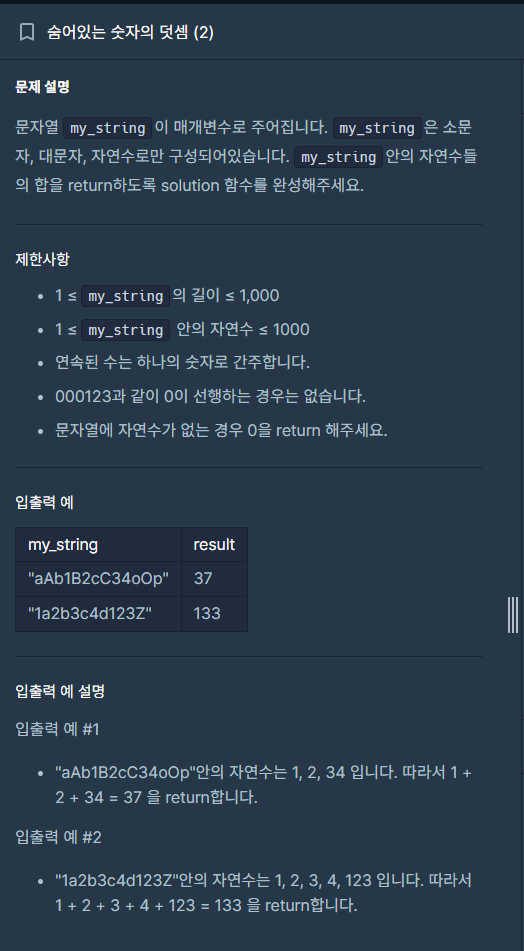
import re

def solution(my_string):
    return sum(map(int, re.findall(r'[0-9]+', my_string)))

정해진 네 가지 발음만 카운트

import re

def solution(babbling):
    count = 0
    p = ["aya", "ye", "woo", "ma"]
    for i in babbling:
        for pattern in p:
            i = re.sub(pattern, ' ', i)
        if i.replace(' ', '') == '':
            count += 1
    return count

정규표현식에서는 주로 findall과 sub를 사용한다. 잘 알아두자.

참고

array과 list의 차이를 알고 있는가?
array은 데이터가 따딱따딱 붙어있고 이어져 있는 자료형이고, list는 데이터가 붙어있지는 않지만 이어져 있는 자료형이다.

빅오 표기법

O(n)과 같이 사용하며, 프로그램을 실행하는 데 걸리는 시간을 표기하는 방법이다.

for문과 재귀 함수 중에 무엇을 많이 쓰는가? 라고 하면은
상황에 따라 다르다고 할 수 있다.

for문
빠른 대신 상대적으로 복잡하다.
재귀
느린 대신 코드가 직관적이다. 재귀 함수를 조금 더 빠르게 하기 위한 메모이제이션이라는 기법이 존재한다.
메모이제이션

dic = {1:1, 2:1}
def fib_memoization(n):
    if n in dic:
        return dic[n]

    dic[n] = fib_memoization(n-1) + fib_memoization(n-2)
    return dic[n]
fib_memoization(5)

# fib(5)
# dic[5] = fib(4) + fib(3)

# fib(4)
# dic[4] = fib(3) + 1

# fib(3)
# dic[3] = 1 + 1

말 그대로 데이터를 저장해 두었다가(캐싱 같은 느낌?) 해당 숫자가 나오면 사용하여 빠른 속도를 추구하는 기법이다.

트리

검색과 같은 기능에 사용한다. 정규표현식으로 걸러낸 문자열을 트리로 찾는 느낌이라 생각하면 편하다.

트리 vs 연결 리스트

트리는 계층적 구조를 가지며, 이전 노드로 이동이 불가능하다. 연결 리스트는 앞/뒤로 이동이 가능하며 선형 구조이며, 순회가 가능하다.

보통 트리가 시간 복잡도는 더 낮다.

종류

포화이진트리

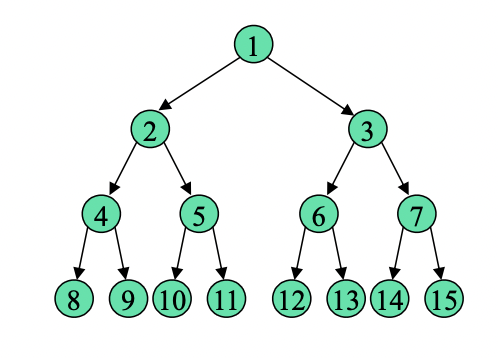
모든 노드가 꽉 차있는 트리이다.
완전 이진 트리

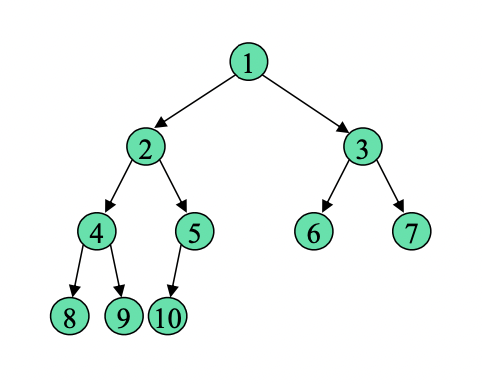
왼쪽부터 순서대로 채워진 트리를 말한다.

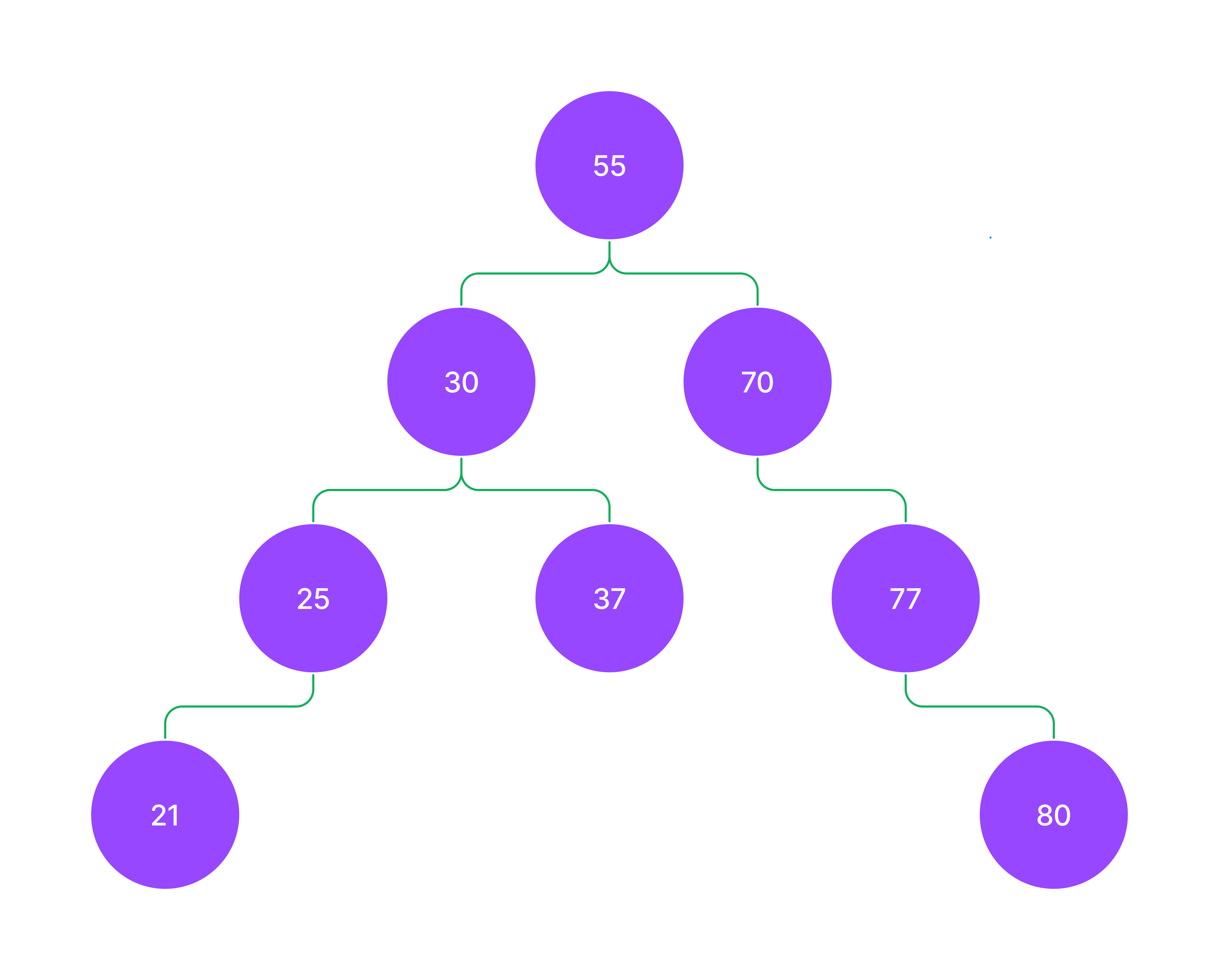
트리 구현

value child-left child-right 값을 가진다. 가장 상위 노드를 루트(root) 라고 하며, 각 층을 깊이(레벨)이라고 한다. 각 층의 마지막에 위치한 노드를 리프(내부, leaf) 노드라고 한다.

# 간단 구현
tree = {
    'root' : {
        'value' : 55,
        'left' : {
            'value': 30,
            'left': {
                'value': 25,
                'left': {
                    'value': 21,
                    'left': None,
                    'right': None,
                },
                'right': None
            },
            'right': {
                'value': 37,
                'left': None,
                'right': None
            },
        },
        'right' : {
            'value': 70,
            'left': {
                'value': 75,
                'left': None,
                'right': None
            },
            'right': {
                'value': 77,
                'left': None,
                'right': {
                    'value': 80,
                    'left': None,
                    'right': None,
                }
            },
        },
    }

현실 세계와 같이 한 부모 아래에 있는 노드만 형제 노드라고 한다.

보통은 다음과 같이 클래스로 구현한다.

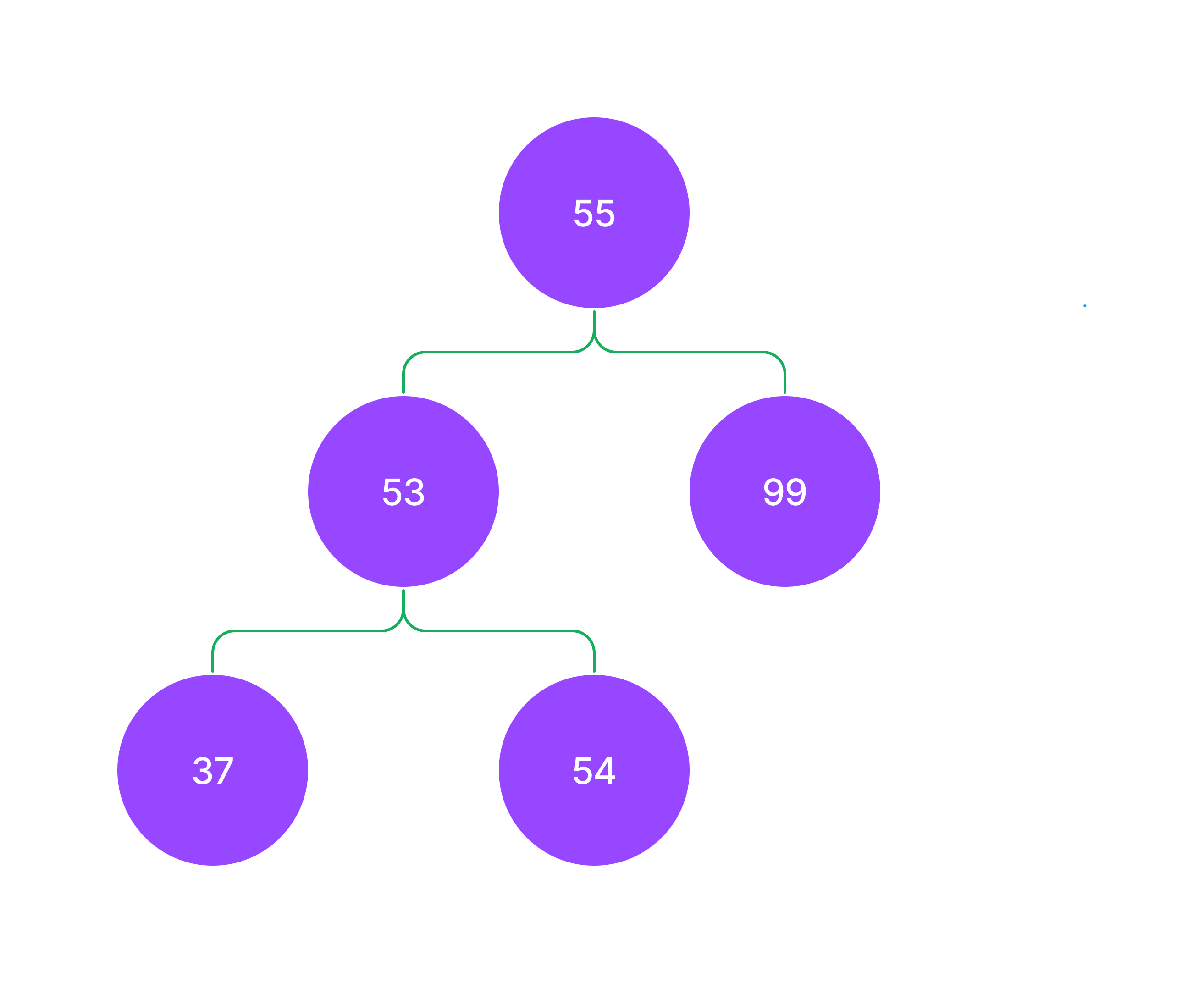
class Node:
    def __init__(self, data):
        self.data = data
        # self.child = [] 2진 트리가 아닌 경우 child를 사용할 수 있습니다.
        self.left = None
        self.right = None

node1 = Node(55)
node2 = Node(99)
node3 = Node(53)
node4 = Node(37)
node5 = Node(54)

node1.left = node3
node1.right = node2
node3.left = node4
node3.right = node5

node1.data
# 55
node1.right.data
# 99
node1.left.data
# 53
node1.left.left.data
# 37