[논문 리뷰] Read this paper if you want to learn logisitc regression

감귤맛젤리·2024년 12월 7일

ABSTRACT

target이 이진 범주형인 경우 - 이항 종속 변수(dichotomous dependent variables)를 다루기 위한 가장 적합한 통계 기법인 로지스틱 회귀에 대한 직관적인 소개
브라질 하원의원 선거에 출마한 후보들의 재선 가능성에 대한 corruption scandals의 영향을 추정하기 위해 Castro and Nunes(2014)의 데이터 를 사용
R에서의 계산 구현을 보여주고 결과의 실질적인 해석을 설명

1. Introduction

종속 변수가 이진인 경우, OLS(Ordinary Least Squares) 모형의 몇 가지 가정(등분산성, 선형성, 정규성)이 위반되며, 이 경우 추정값이 일관성이 없을 수 있다. 가정이 위반될 경우에는 데이터의 특성에 더 적합한 기법을 채택해야 한다.

📌 이진 종속 변수를 다루는 데 가장 적합한 도구는 로지스틱 회귀이다. 즉, y가 두 가지 categories만 취할 수 있을 때, 로지스틱 회귀가 적합하다.

e.g. 당선 또는 낙선, 정책 채택 또는 미채택, 투표 하거나 하지 않은 경우 등

방법론적으로, Castro and Nunes(2014)의 데이터 를 재현하여 2006년 브라질 연방 하원의원 선거에 출마한 후보들의 부패 스캔들 관련 참여와 재선 가능성 간의 관계를 분석한다.

마지막에는, 독자들은 이해할 수 있다:

로지스틱 회귀가 언제 사용되어야 하는지
모델을 계산적으로 구현하는 방법
결과를 해석하는 방법

논문의 나머지 부분의 구성:

로지스틱 회귀의 기본 특징
모델의 추정값이 일관성을 유지하기 위해 충족되어야 하는 주요 기술적 조건 식별
관찰해야 할 주요 통계
브라질 정치학 학생 및 대학원 학생들에게 제공되는 방법론적 교육의 질을 향상시키기 위한 몇 가지 권장 사항

2. The logic of logistic regression

로지스틱 회귀에서 종속 변수는 두 가지 범주만 가진다. 일반적으로 사건의 발생은 1로, 발생하지 않음은 0으로 코딩된다. 코딩 방식에 따라 계수의 signal이 변경되며, 실질적인 해석도 달라진다. 로지스틱 회귀가 어떻게 작동하는지를 이해하기 위해서는 회귀 분석의 논리를 전반적으로 이해해야 한다.

선형 모형의 고전적인 표기법을 살펴보면:

Y = \beta_0 + \beta_1X +\epsilon

Y 는 종속 변수이며, 우리가 이해/설명/예측하려는 대상이다.
X 는 독립 변수이다.
절편(intercept)은 X가 0일때의 Y값이다.
회귀 계수는 X가 1단위 증가할 때 Y에서 관찰되는 변화를 나타낸다.
확률적 항(stochastic term)은 모델의 오류를 나타낸다.

기술적으로, 종속 변수와 여러 독립 변수 간의 선형 관계를 추정할 수 있다. 또한, 이 모델은 효과의 크기를 관찰하고 계수의 통계적 유의성(p-value 및 신뢰 구간)을 검정(test)할 수 있다.

로지스틱 회귀는 종속 변수가 이진인 일반화 선형 모형(GLM)의 특별한 경우로 해석할 수 있다.
Linear regression line versus logistic curve

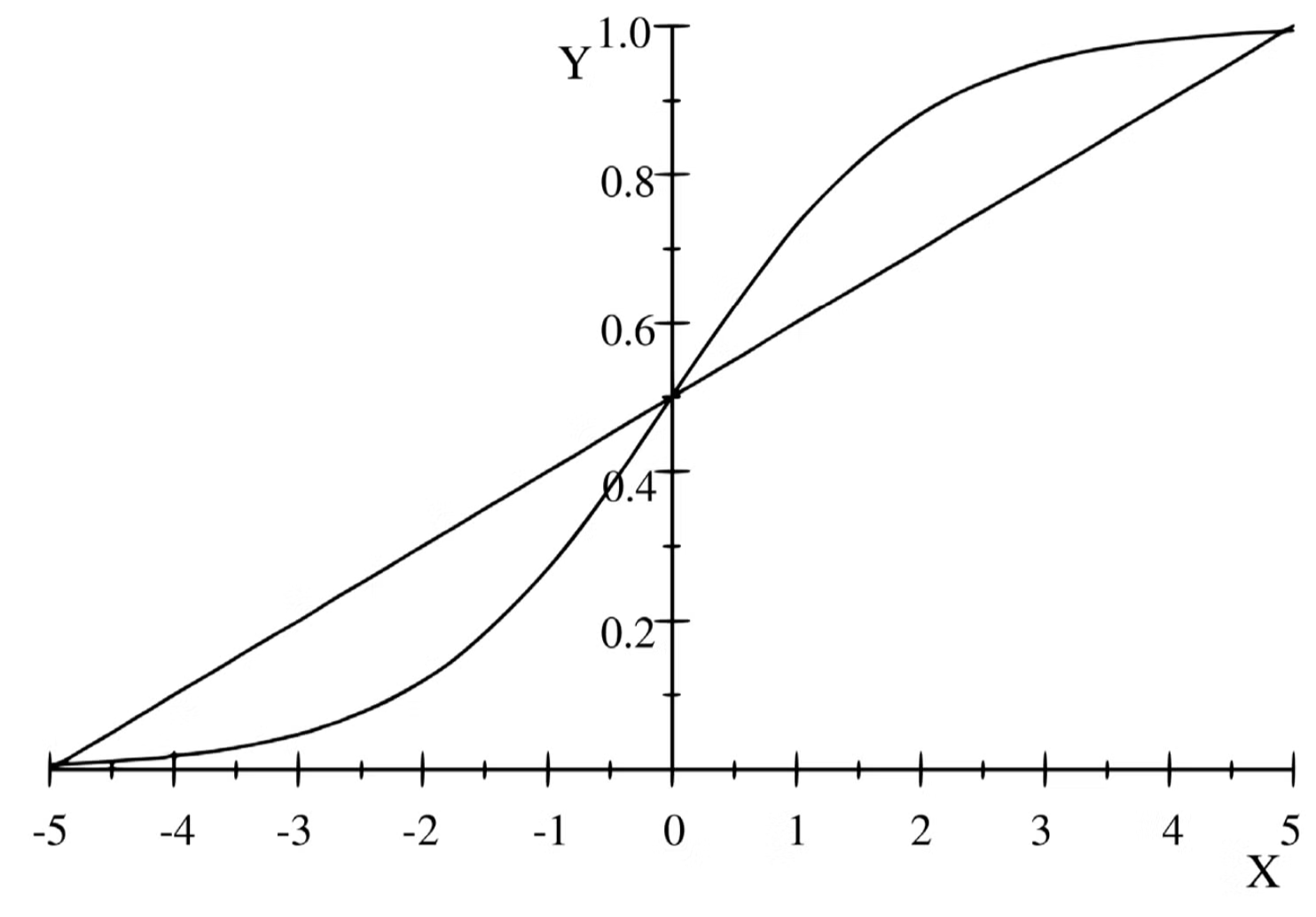
로지스틱 모델에서 종속 변수가 두 값(0, 1)만 취하므로, 모델이 예측하는 확률도 해당 구간에 제한되어야 한다. X(독립 변수)가 낮은 값을 가질 경우, 확률은 0에 가까워지고, X가 증가함에 따라 확률은 1에 가까워진다. 종속 변수의 이진적 특성은 선형 모델의 몇 가지 가정(등분산성, 선형성, 정규성)을 위반하므로, 이진 변수를 분석하는 데 선형모델을 사용하는 것은 비효율적이고 편형된 계수를 초래할 수 있다.

Age x coronary disease

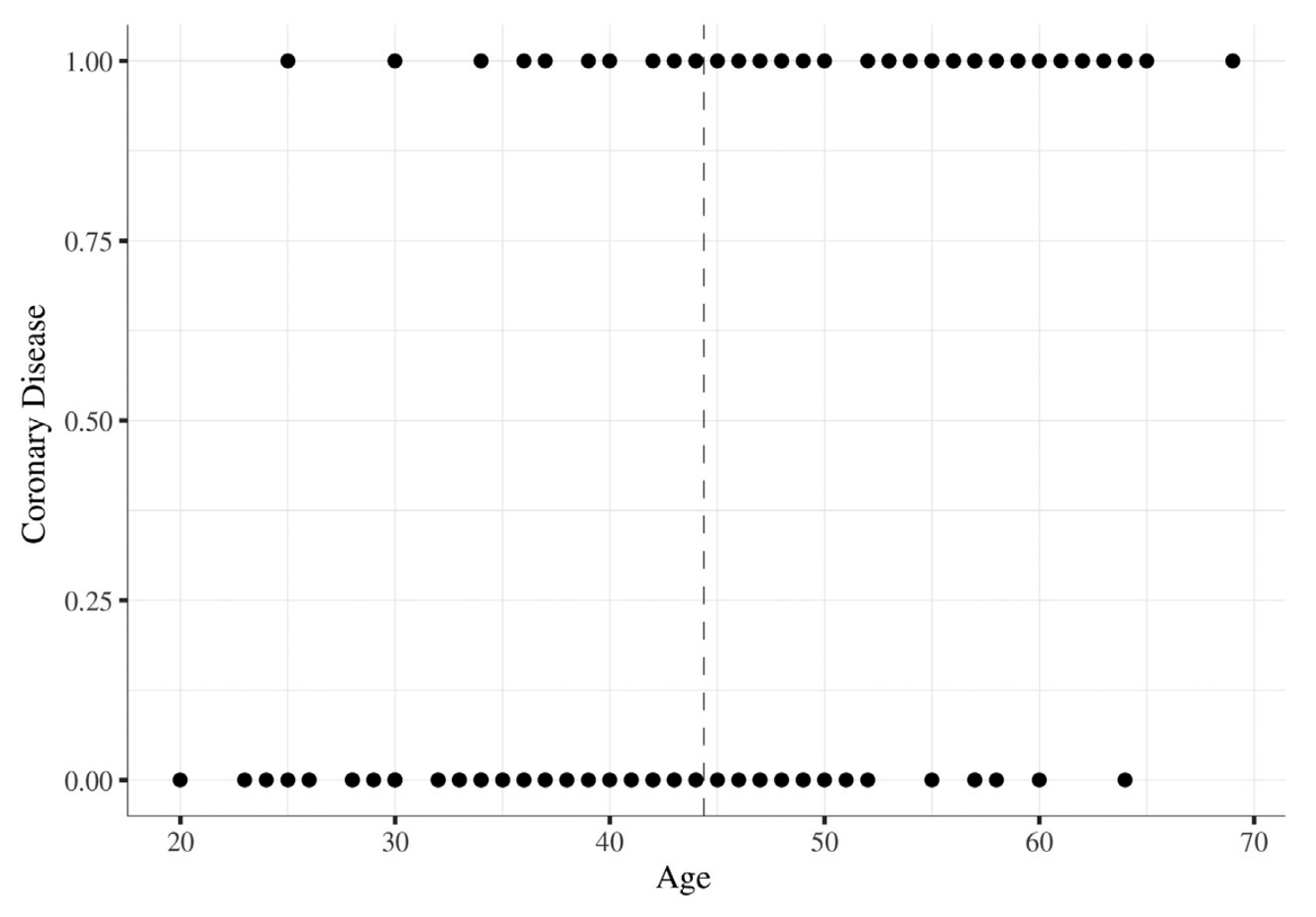
수직 점선은 평균 나이(44.38), 사례는 1(관상 동맥 질환 발생) 0(발생하지 않음)으로 코딩되었다. 나이가 증가함에 따라 관상 동맥 질환 진단을 받은 사람의 수가 증가한다.

직관적으로 이 패턴을 관찰하는 방법은 평균을 비교 기준으로 사용하여 사례 수를 살펴보는 것
a. 평균 이상인 사람들에서 질병 사례가 더 많고, 평균이하는 발생하지 않음 범주에 더 많음
⇒ 그래프는 나이와 관상 동맥 질환 간의 연관성이 있음을 나타낸다.

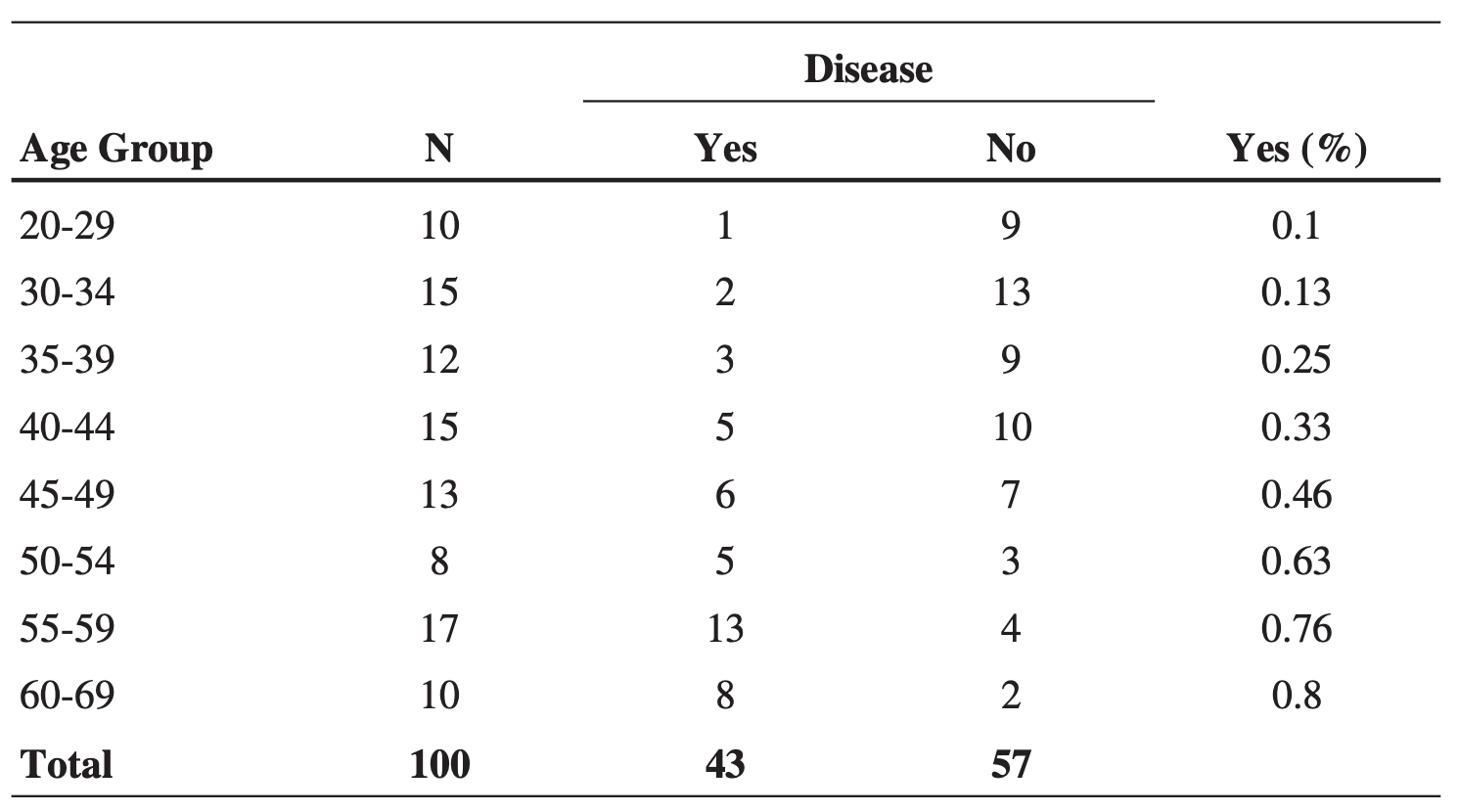
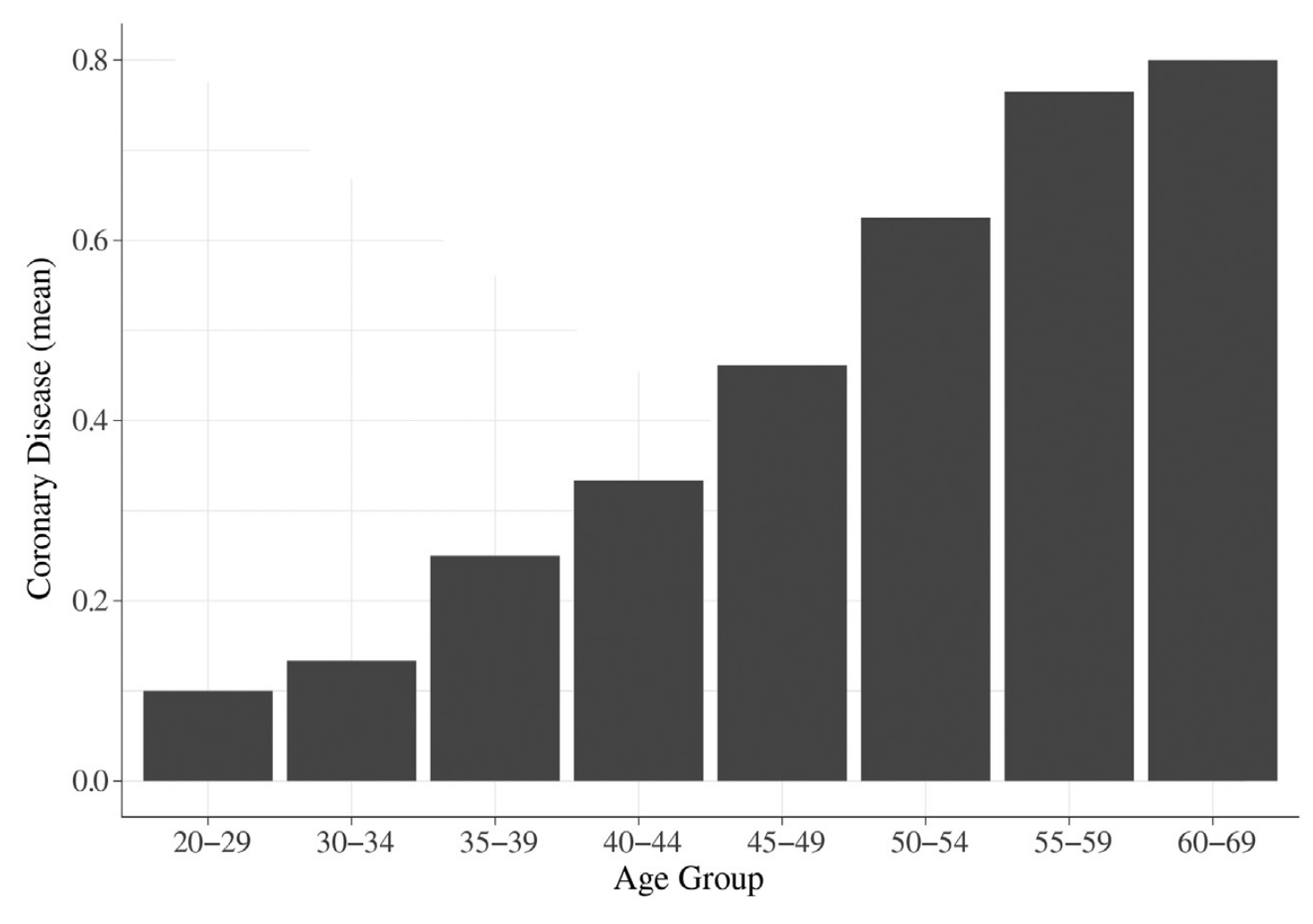
나이와 심장 질환 발생 확률간의 positive correlation을 확인할 수 있다.

로지스틱 회귀는 이 관계의 방향, 크기 및 통계적 유의성 수준을 알려준다.

통계적 유의성 수준 : 통계 분석에서 결과가 우연에 의해 발생할 가능성이 낮다는 것을 나타내는 지표. 보통 p-value로 표현되며, 특정 유의 수준(0.05) 이하일 경우 결과가 통계적으로 유의하다고 판단한다.
=> 관측한 결과가 통계적으로 의미 있는지를 평가하는 기준 = 신뢰할 수 있다.
즉, 종속 변수가 범주형이고 이진일 때 연구자는 로지스틱 회귀를 사용해야 한다.

3. Planning a logistic regression

1️⃣ 첫 번째 단계 : 종속 변수가 naturally dichotomous인 research question을 식별하기

e.g. 건강 연구 : 생존/사망, 아픔/건강, 흡연자/비흡연자

보통은 연속형(continuous) 또는 이산형(discrete) 변수를 범주형으로 recoded하는 것을 포기해야 한다. 기술적으로, 수량형 변수를 범주형으로 재코딩하는 것은 정보 손실을 의미하며, 이는 추정치의 일관성을 감소시킨다.

e.g. 소득을 재코딩하여 두 가지 범주인 부유한 사람과 가난한 사람으로 나누는 것은 잘못 나눈 것

2️⃣ 두 번째 단계 : 기술적 요구사항 준수하기

📌 다중 공선성

독립 변수 간 높은 상관관계

로지스틱 회귀에서는 샘플 크기가 핵심이다. 작은 샘플은 추정치가 일관성이 없어지고, 지나치게 크면 모든 효과가 통계적으로 유의미해진다. 독립 변수 중 하나를 단순히 제거해서는 안되고, 관측치 수를 늘리거나 데이터 축소 기술을 사용한다.

⇒ 최소 400개의 사례가 필요하고, 독립 변수당 10개의 사례 비율, 초정된 매개변수에 대해 30개의 사례 비율을 추천한다.

📌 이상치(outliers)

극단적인 사례는 데이터 분석에서 재앙적인 결과를 초래하므로, 아래의 방법이 있다.

모델의 추정에서 이상치를 제외하고, 계수에 미치는 영향 측정하기
사례를 재코딩하여 덜 극단적인 값, 예를 들면 평균을 적용하는 것 ✨

3️⃣ 세 번째 단계 : 연구자가 모델을 추정(estimate)

사용한 소프트웨어를 report
원본 데이터, 조작된 데이터, computational scripts를 포함하는 replication materials 공유

⇒ 필수적인 절차

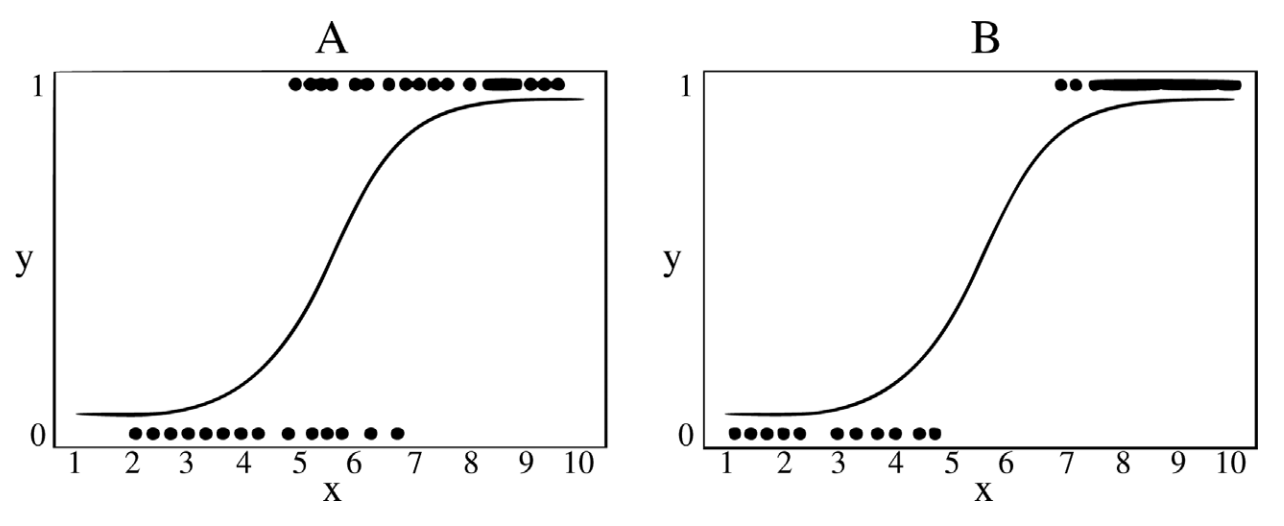
                            comparing the fit of logistic models

위의 그림은 로지스틱 회귀를 사용할 때 모델 비교의 기본 논리를 보여준다. 비교적 모델 B는 모델 A보다 더 나은 적합도를 가지는데, 이는 판별럭의 차이(discriminatory power)로 관찰할 수 있다.

가장 단순한 모델(상수만 포함)은 예측 변수가 없어서 성능이 낮고, 복잡한 모델은 모든 예측 변수와 상호작용까지 포함해 성능이 좋을 수 있지만 항상 그런 것은 않으니 다양한 모델을 만들어 어떤 모델이 데이터를 잘 설명하는지를 확인해봐야 한다.

📌 연구자는 적합도 검정을 사용하여 가장 적은 수의 예측 변수를 사용해 가장 예측을 잘 수행하는 모델을 선택한다.

네 번째 단계 : 결과의 해석

📌 통계적 유의성 뿐만 아니라 계수의 해석도 중요하다.

다만, 계수가 직접적으로 사건의 발생 확률을 보여주지 않기 때문에, 계수가 쉽게 해석되는 선형 회귀와 달리 로지스틱 모델에서 생성된 추정치는 덜 직관적이다.

선형 회귀 vs 로지스틱 회귀 선형 회귀는 계수가 변수의 변화에 따른 직접적인 영향을 쉽게 해석이 가능 로지스틱 회귀는 로그 오즈의 변화를 기반으로 하기 때문에 계수의 변화가 사건의 확률에 미치는 영향을 이해하는 데 추가적인 계산이 필요 e.g. 계수 0.6 X값 1증가 → Y의 로그 값이 0.6증가

⇒ 로그 값이 0.6 증가했다는것은 직관적이지 않고 변수 간의 관계를 이해하기 어렵다.

📌 계수 자체의 지수를 구해 독립 변수가 Y의 오즈에 미치는 영향을 분석한다

0.6의 지수는 1.82이다. (e^0.6) → x가 1단위 증가 시 y가 발생할 확률이 1.82배 증가한다는 의미(다른변수는 일정하게 유지)한다.

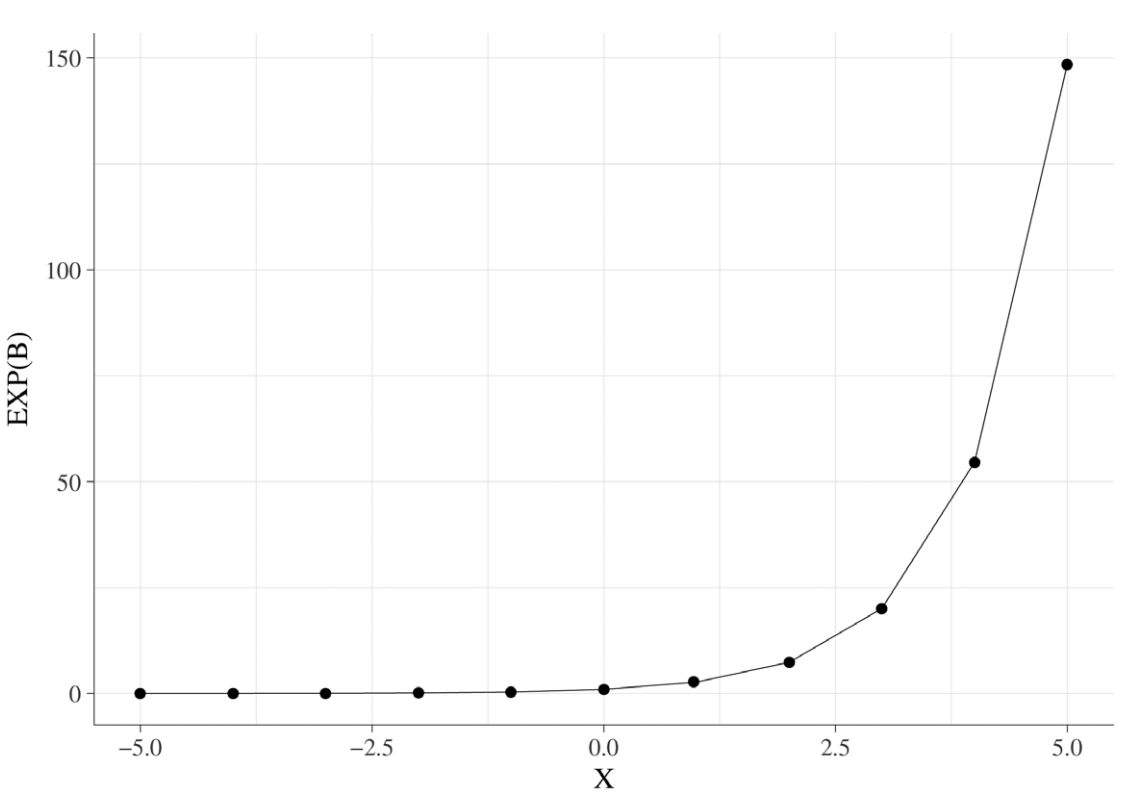
                                     Exponential function

exp(0.6) = e^{0.6}\approx 1.82

로지스틱 회귀에서 1보다 큰 계수를 넣으면 양수의 지수를 생성하고, 음수 계수는 exp가 1보다 작은 값을 반환한다. 값이 0이면 영향을 미치지 않는다.

⏩ 계수가 1에서 멀어질수록 방향에 관계없이 특정 독립 변수가 관심 있는 사건 발생 확률에 미치는 영향이 커진다.

📌 Y 발생 확률의 백분율 증가 추정

(지수화된 회귀 계수 (1.82) - 1 )*100

→ x의 1단위 증가는 Y발생 확률을 82% 증가시킨다.

로지스틱 회귀 계수의 해석은 계수(β)가 음수인 경우 복잡한데(exp값이 1보다 작아 독립 변수가 증가할 때 종속 변수가 발생할 확률이 감소하는 것을 나타내기 때문) 계수를 반전시켜 (1/계수의 값)으로 해석을 하면 쉽게 해석이 가능하다. (1단위 감소할 때, 1.56배 증가한다)

\frac{1}{0.639} \approx 1.56

📌 원본 데이터셋의 하위 샘플을 사용하여 관찰 결과를 검증

특히 작은 샘플로 작업할 때 연구 결과의 신뢰성을 높인다.

4. An applied example

2006년에 재선된 후보자에게 1값을 부여, 그렇지 않은 경우 0을 부여할 종속 변수를 식별하기
로지스틱 회귀를 추정하기 위한 기술적 요건 확인하기
1. 이상치, 다중공선성, 적절한 샘플 크기 관찰
2. 217개의 관측값과 각 독립 변수당 19개의 사례 비율을 갖는다. (217개의 관측값후보자 데이터가 있고, 19개의 사례비율독립 변수에 각각 19개의 사례가 있다는 의미)
모델의 추정
$logit(Y)=logit(Y) = \alpha + X_1 \beta_1 + X_2 \beta_2 + X_3 \beta_3 + X_4 \beta_4 + X_5 \beta_5 + X_6 \beta_6 + X_7 \beta_7 + X_8 \beta_8 + X_9 \beta_9 + X_{10} \beta_{10} + X_{11} \beta_{11} + \epsilon$

변수들이 어떻게 측정되었는지 요약

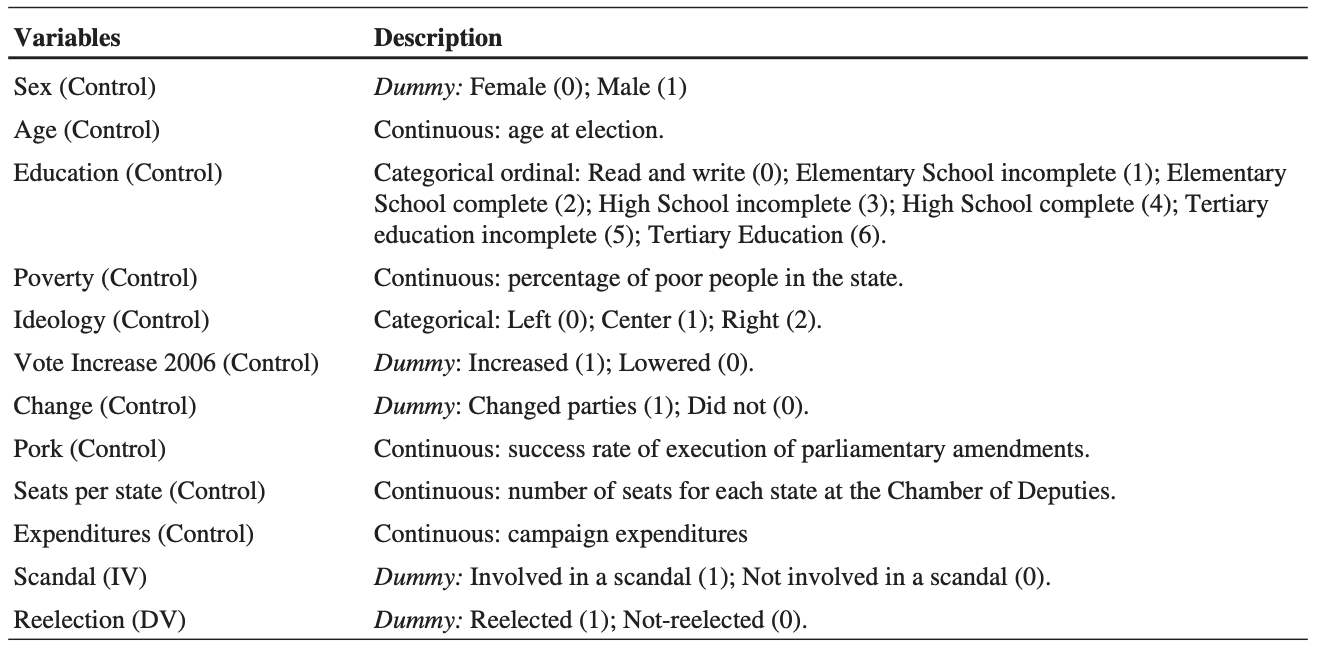
세 가지 가설 검증
H1 : 부패 스캔들에 연루되는 것은 재선 확률을 줄인다.
H2 : 캠페인 지출이 높을수록 재선 확률이 높아진다.
H3 : 수정안의 실행이 높을수록 재선 확률이 높아진다.

5. Result

1️⃣ 종속 변수의 분포 분석하기

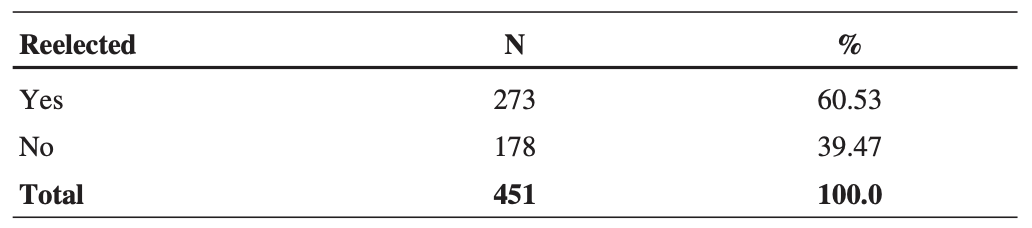
451개의 사례가 있고, 연방 의원의 60.53%가 재선되었으며, 273회의 사례가 있다.

\frac{0.395}{0.605} = 1.53

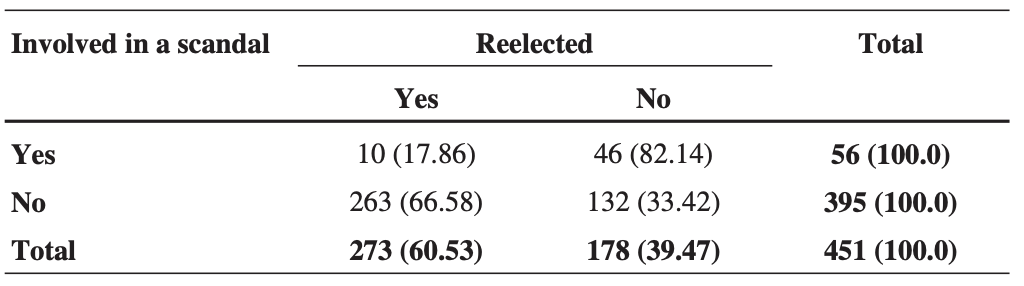
→ 재선될 확률이 재선되지 않을 확률에 비해 약 1.53배 높다는 것을 의미한다.

부패 스캔들에 연루된 후보자만 고려할 때, 재선율은 17.86%로, 56명의 대표 중 10명이 재선됐다.

이는, 이 그룹의 경우 재선 확률이 0.197이며 재선의 가능성이 0.22임을 의미한다.

재선 확률은 특정 그룹이 재선될 가능성(그룹 내에서 실제로 재선된 비율)을, 재선 가능성(그 그룹의 재선 가능성을 비교한 수치)은 해당 그룹이 재선될 확률과 재선되지 않을 확률의 비율

부패 스캔들에 연루되지 않은 후보자의 경우 재선 확률은 1.9이다.

2️⃣ 모델의 적합성 평가

Hosmer and Lemeshow 테스트를 사용한다.

연속 독립 변수가 있거나 샘플 크기가 작은 경우 유용하다.

                               Homer and Lemeshow Test

chi-square은 6.832, p-value는 0.555 → 적절한 적합성

chi-square(카이제곱) 관측된 빈도와 기대되는 빈도 사이의 차이를 나타내는 값 → 클수록 두 빈도 간의 차이가 크다.

✅ omnibus test of model coefficients

모델의 분산을 독립 변수와 영모델(단순 절편)과 비교하는 chi-square test이다.

                         Omnibus test of model coefficients

chi-square of 56.356 (p-value < 0.001) → fitted model이 null model보단 좋음을 의미

⇒ 독립 변수가 종속 변수의 변동에 영향을 미친다고 결론

📌 추정된 계수(β) 분석

추정의 부호를 관찰하고 자신의 가설에서 기대하는 방향과 비교해야 한다.

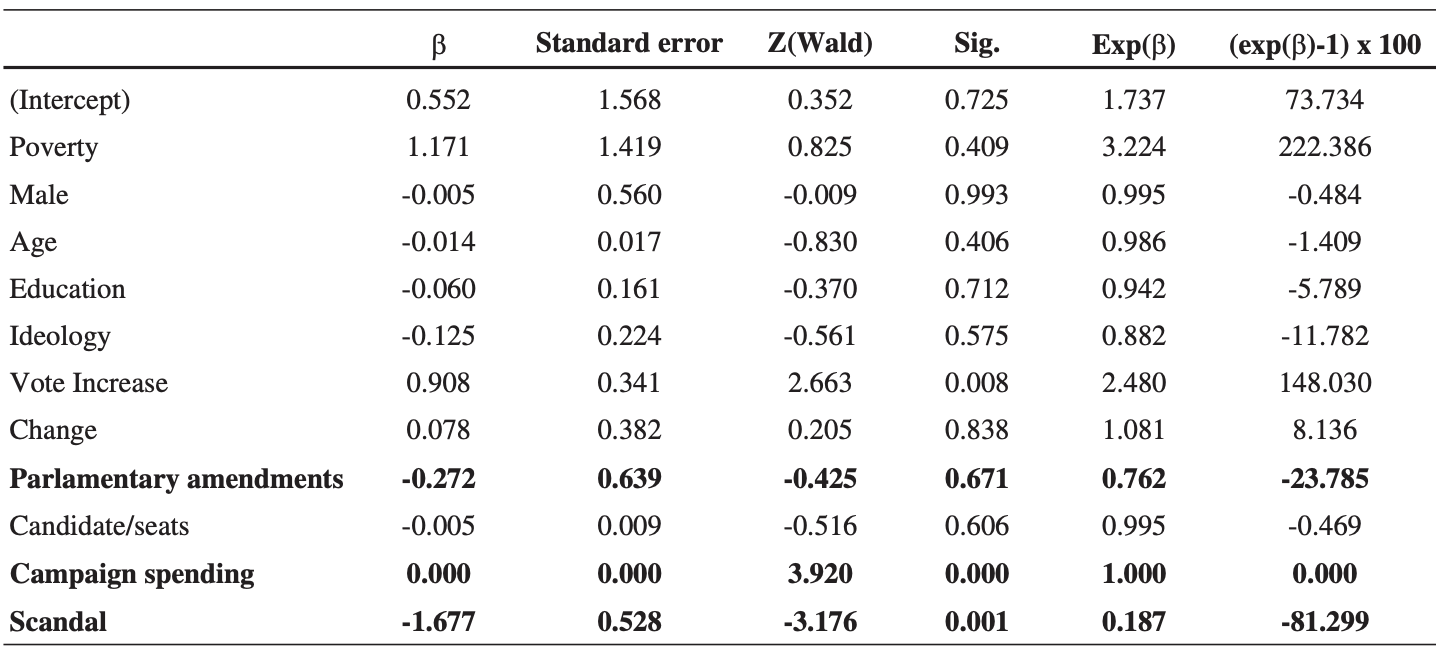
X_11(스캔들)은 재선 확률에 부정적인 효과 (-1.677)을 미친다.

✔️ 계수를 읽는 두가지 방법

오즈비 분석(Odds ration)

오즈비를 백분율로 전환(Odds ration into a percentage)

오즈비 분석 : 부패 스캔들에 연루되면 선출될 가능성이 줄어든다고 결론

오즈비 백분율 : 부패에 연루되면 재선 확률이 80.2% 감소하고, 가설 1 예상 적중✨

캠페인 비용을 고려할 때 효과는 없다. (Exp(β) = 1.000)
의회 수정안 변수의 유의미한 효과가 없는 이유는 p값의 크기와 표준 오차가 영향 추정치(회귀계수)의 두 배 이상 크기 때문이다.

최대 우도에 의해 추정된 모델에서 일반적으로 보고되는 적합도 측정치를 요약

최대 우도 (Maximum Likelihood) : 관측한 데이터를 가장 잘 설명할 수 있는 파라미터를 찾는 것
-2 log likelihood(-2LL) : 모델의 적합도를 측정하는 지표 중 하나 - 값이 작을수록 좋다.
카이제곱 : 두 모델 간의 차이를 비교하기 위해 사용하는 통계량 - 값이 클수록 모델 간 차이가 크다
- null model과 적합 모델의 -2LL을 생성하고, 차이는 카이제곱으로 측정
- 카이제곱이 클수록 적합 모델의 오류 감소가 null모델에 비해 크다

독립 변수를 포함한 모델이 null모델보다 더 우수한 적합성을 가지고 있다.

BIC(bayseian Information Criterion)
- 최대 우도에 기반한 또 다른 측정치인데, 값이 작을수록 좋다.

✔️R²(결정계수)

선형회귀 모델이 데이터를 얼마나 잘 설명하는지 보여주는데 로지스틱회귀 모델 같은 비선형 모델은 R2 사용이 어려워 유사 R2(pseudo R2)를 이용한다.

R² = 0.8 이면 모델이 데이터 변동 중 80% 설명한다는 의미

높다고 좋은 건 아님 - 과적합 가능성 존재

Cox & Snell R²
- 로지스틱 회귀에서 기본적인 유사 R2 지표
- 모델의 우도를 기반으로 계산된다.
- 0과 1 사이의 값을 가지지만, 최댓값이 1보다 작을 수 있다.
Nagelkerke R²
- Cox & Snell R² 보완 위해 개발된 지표
- Cox & Snell R²를 보완하여 최댓값이 1이 될 수 있도록 조정
- 1에 가까울수록 데이터를 잘 설명하는 것

3️⃣ 분류표 분석

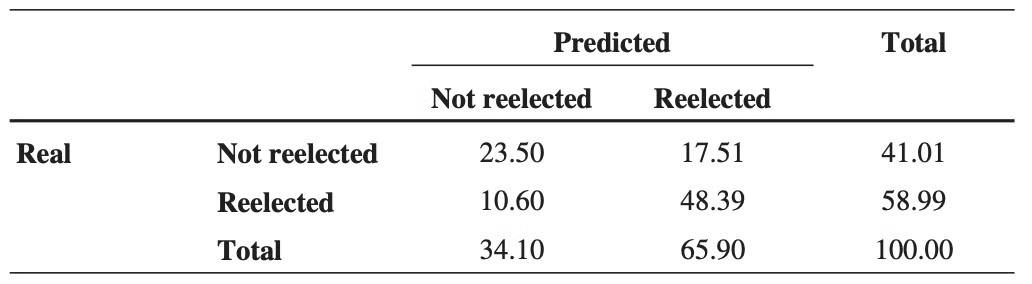
               The classification table - confusion table이라고도 불린다.

예측 확률이 0.5보다 크면 1, 작으면 0으로 할당하는 기존 표준인 50%를 사용한다.
정확도, 민감도, 특이도라는 세 가지 개념을 사용하여 평가가 가능하다.

정확도 : TP, TN 비율 - 71.89%(23.50% + 48.29%)
민감도 : TP/FP+TP - 82.03% (48.39%/58.99%)
특이도 : TN/FN+TN - 57.30% (23.50%/41.01%)

민감도와 특이도는 하나가 증가하며 다른 하나는 감소하므로, 어떤 것이 더 중요한지 판단이 필요하다.

6. Conclusion

로지스틱 회귀 분석의 직관적인 논리를 이해하는 것이 범주형 데이터를 처리하는 다양한 절차를 더 잘 이해할 수 있는 발판이 될 수 있다.

인식론과 과학 철학 과목, 데이터 분석 실습 진행, 고급 데이터 분석 기법을 사용하는 논문을 읽는 것 확산, 미적분, 선형 및 행렬 대수, 고급 통계학 공부가 필요하다.

감귤맛젤리

이전 포스트