Machine Learning Basic, Linear Regression
Deep learning
: 머신러닝에서 쓰이는 학습 방법을 차용해서 머신러닝 알고리즘들이 성능을 더 잘 올릴 수 있도록 도와주는 feature extractor이다.
Categories of ML problems
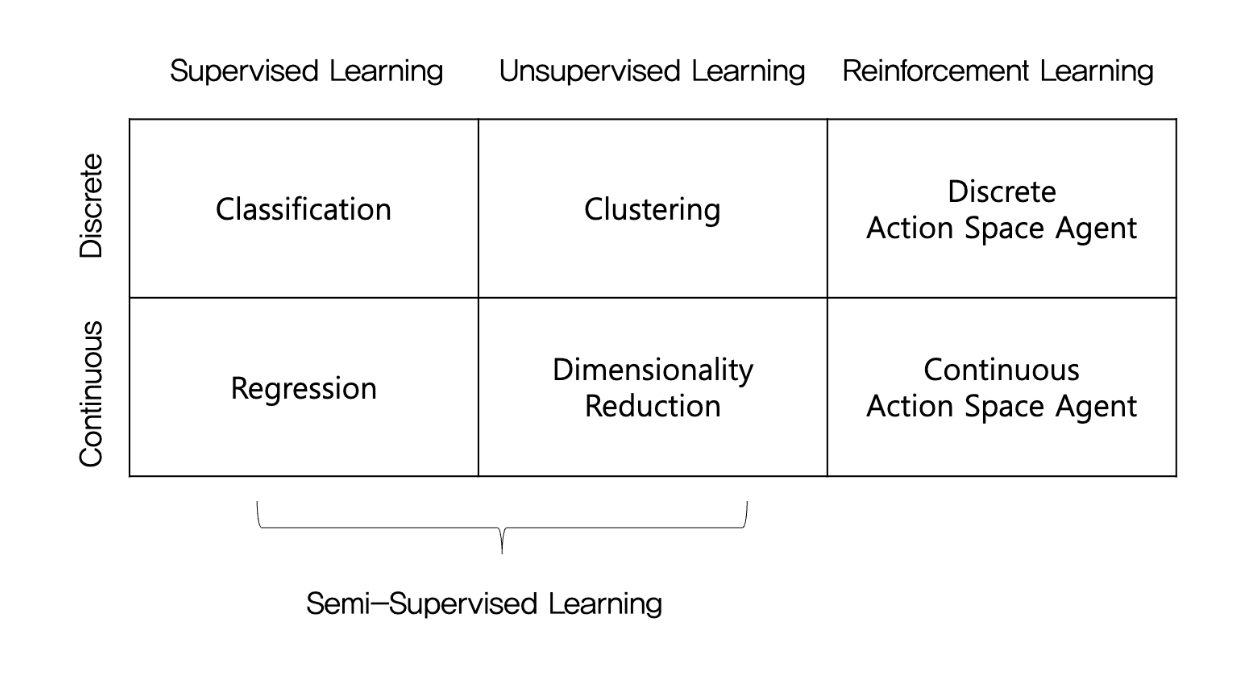
semi supervised learning
일부 데이터에 대해 라벨링(x, y전부 존재, 지도학습)을 진행 후 클러스터링한다. 노래를 분류하는 작업이 있는데 10000개 중 100개는 라벨링을 해주는 것(힌트)이다.
전체를 대변하지는 않지만, supervision을 제공할 수 있다. 또한, 요즘 많이 이용하는 추세인데 현실에서의 데이터는 항상 라벨링되어있지 않기 때문이다.
Regression vs Classification
📍Classification
분류의 y는 class이다. 즉, 어떤 class(대상)에 속하는지 예측한다. 예를들어, 개/고양이 이미지 예측이 있다.
1. 이진 분류(Binary classification) : class가 2개
스팸메일인지/아닌지 등 예/아니오로 구분될 수 있는 문제들을 주로 포함한다. positive class, negative class로 나눌 수 있고 주로 학습하고자 하는 대상을 positive class로 부르기도 한다. 욕설인지/아닌지 분류 시 욕설class가 positive class가 된다.
- 다중 분류(Multi-class classification) : class가 여러개
언어 분류 모델의 경우 입력 text가 영어/프랑스어/독일어/한국어인지 분류한다.
📍Regression
회귀의 y는 연속적인 숫자, 즉 예측값이 float형태이다. 예를들어 지하철 역과의 거리, 일정 거리안의 관공서, 마트, 학군 수 등의 여러 feature들로 지역의 땅값을 예측하는 문제가 있다. 땅값이 평당 1천만원, 1.1천만원 이여도 무한한 실수들 중에서 대푯값을 선택한 것이므로 회귀이다.(평당 10,000,001원과 10,000,002원은 큰 차이가 나지 않지만 다른데, 대푯값인 1천만으로 표현하는 것)
⚠️구분 시 주의점
분류는 class 예측, 회귀는 연속적인 값에서 한 점을 찍는 것인데 score(가능성)으로 y를 잘못 생각하면 문제가 발생한다.
욕설인지 아닌지 예측하는 문제는 이진 분류 문제이므로 욕설인 데이터와 욕설이 아닌 데이터를 수집하고 모델링해 각 class(욕설/정상)에 속할 확률을 계산하고, 확률이 더 높은 class를 최종적으로 예측한다. softmax처럼 모델이 두 class(욕설/정상)의 확률 합이 1이 되도록 확률을 출력한다.
그러나 욕설에 대한 데이터만 수집 후 입력이 욕설일 가능성(특정 feature이 관찰된 빈도를 기반으로 계산한 score)을 계산하는 문제로 접근하게 되는 경우가 있는데, y가 float이라 회귀로 착각할 수 있지만, 이는 분류나 회귀의 문제가 아니다. y가 class나 값이 아닌 욕설일 가능성을 나타내는 숫자(score)이기 때문이다. score은 출력 값이 일정 범위 안에서 정규화되지 않아 threshold을 주관적으로 설정해야 하는 문제가 발생한다. relu나 sigmoid함수를 통해 정규화 하더라도 최댓값을 모르므로, 어느정도가 1을 넘는지 알 수가 없다.
즉, 욕설 예측 문제는 분류로 접근해야 하며, 회귀처럼 착각하거나 임의의 score로 혼동하면 안된다.
회귀는 확률을 예측하는 것이 아니다. 회귀의 y는 연속성이 있고, 그 연속성 중에 어디에 점을 찍을지를 결정하는 문제이다.
확률은 사건들의 연속, 독립, 반복 등의 시행에 따라 표본공간(sample space)속에서 사건이 발생할 경우의 수를 구하는 문제이다.
Dimensionality Reduction
similarity나 distance를 계산할 때 Euclidean Distance를 기반으로 계산하는데, 차원이 높아질수록 고차원의 스페이스에서 계산되는 Euclidean Distance가 의미 없어지는 현상인 차원의 저주가 발생한다.
따라서 데이터의 손실을 막고, 저차원의 공간으로 보내려는 노력을 해서 차원을 축소하려고 노력한다.
PCA(Principal Component Analysis, 주성분 분석)
분산은 데이터가 평균으로부터 얼마나 퍼져 있는지를 나타내는데, 데이터의 분산이 크다는 것은 데이터가 여러 방향으로 넓게 퍼져 있어 서로 덜 겹치고, 더 독립적이라는 뜻이다.
PCA는 데이터를 고차원에서 저차원으로 projection하면서 데이터의 정보를 최대한 유지하기 위해, 데이터의 분산이 가장 큰 축(principal component, 주성분)을 자동으로 찾아 space의 basis로 삼아 projecion을 한다. 주성분은 차원에 따라 여러 개가 존재하는데, 두 번째 주성분은 첫 번째 축에 직교하면서 분산이 두 번째로 큰 방향이다.
분산이 가장 큰 축으로 projection하기 때문에 데이터의 loss를 최소화하면서 차원을 줄일 수 있다.
⇒ 데이터가 덜 겹쳐 있으니 해당 기준으로 데이터를 바라보면 차원 축소 시 데이터 손실을 줄일 수 있다는 의미이다.
차원 축소는 다른 알고리즘과 같이 많이 사용된다.
Cost Function(Loss Function)
직선과 y의 거리인데, 그냥 무턱대고 빼버리면 음수가 있어 로스 합이 0이 되는 등 제대로 반영이 안될 수 있기 때문에 오차에 절댓값이나 제곱을 취한다.
simplified hypothesis (b 제거)
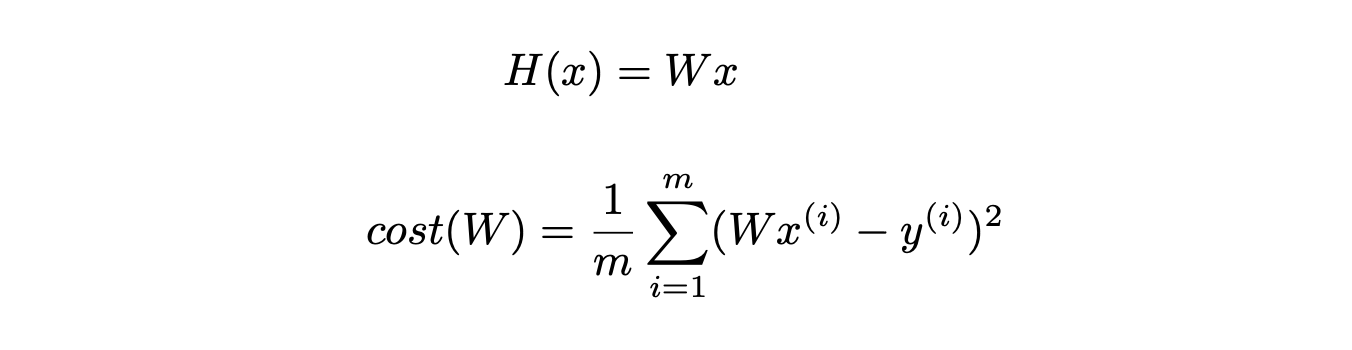
x는 데이터이기 때문에 상수처럼 작동이 되는데 W로 인해 값이 변경된다.
Gradient descent algorithm
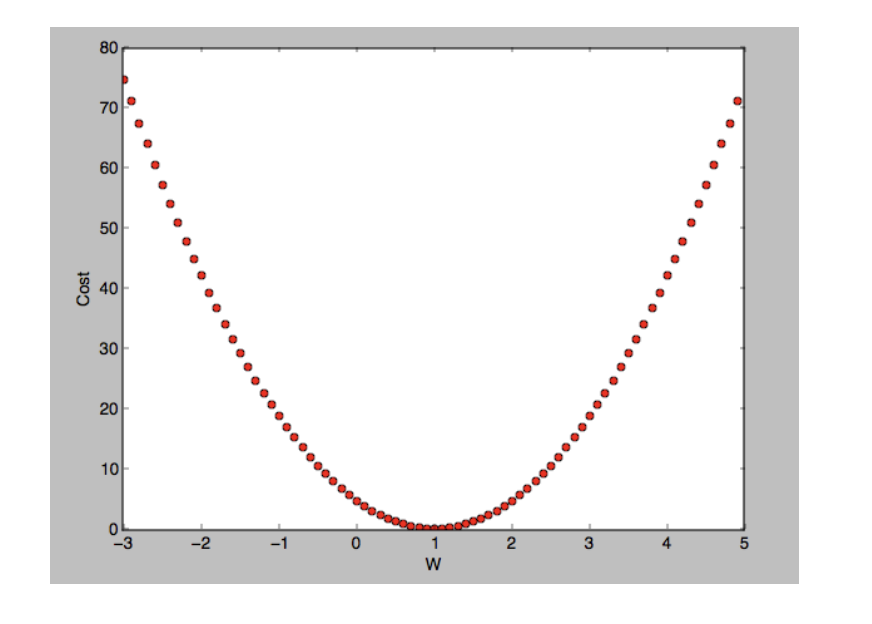
랜덤한 특정 점을 찍고, 미분계수가 줄어드는 방향으로 W - 해당 W에서의 미분계수를 해주되, 미분계수 바로 빼버리면 한 번에 너무 많이 이동해 버리기 때문에, learning rate라는 작은 값을 곱해줘서 조정해준다. 즉, W=4의 미분계수가 5이고, learning rate가 0.01이라면, 5에서 줄어드는 방향으로 진행되어야 loss가 줄기 때문에 4 - 5*0.01 = 3.95 가 다음 W값이 된다. 해당 과정들을 반복해 loss가 최소일때의 W를 구한다.
하지만, 수치해석적으로 W마다 직접 계산을 하면 시간이 오래 걸릴 수 있고, 다차원 문제에서는 복잡도가 매우 높아지므로 실제로는 편미분을 사용해 특정 변수만 고정하고 빠르게 gradient를 계산할 수 있다. (W에 대해 미분)

📍문제점
1. Global minimum과 local minimum 구분이 어렵다. 특히 비선형 함수에서는 여러 개의 local minimum이 존재할 수 있으므로, 시작점을 다르게 설정하여 결과를 비교하는 것이 중요하다.
2. gradient descent는 시작을 어디서 하느냐에 따라 종착지가 달라질 수 있으므로, 5번 등 랜덤으로 반복 돌려봐서 실험 결과의 평균을 내는 등으로 해결할 수 있다.
🔖참고자료
https://github.com/heartcored98/Standalone-DeepLearning/tree/master?tab=readme-ov-file
https://nexablue.tistory.com/29