문제

BOJ 1932, 정수 삼각형

핵심

• 입력의 크기가 $500$이라 대략 $O(N^2)$ 이하의 알고리즘을 사용한다.
• 아래 그림을 볼 때, 맨 윗층 7부터 시작해서 아래에 있는 수 중 하나를 선택해서 내려갈 때 선택된 수의 합을 최대가 되는 경로를 구해야 한다. 단, 아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다.
  
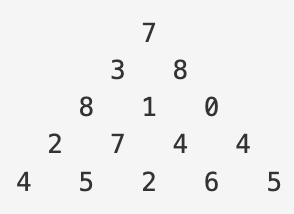
• 규칙을 살펴보면 위에서부터 최대 수를 선택한다고 하더라도 제일 밑에 4대신 100이 있다면 100을 선택해야 한다. 즉 아래 밑변을 모두 고려할 수 있게 점화식을 세워야 한다.
• dp[i][k]: 삼각형 i번째 줄을 k번째 수를 선택했을 때 최댓값. 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서 선택될 수 있으므로 이는 max(dp[i - 1][j], dp[i - 1][j - 1]) + k번째 수로 구할 수 있다.

개선

코드

시간복잡도

• $O(N^2)$

C++

#include <iostream>
#include <algorithm>
using namespace std;

int dp[504][504];
int main(void) {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);	
	int n;
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= i; ++j) {
			int num;
			cin >> num;
			dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1]) + num;		
		}
	}
	cout << *max_element(dp[n], dp[n] + n + 1);
}

Java

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int[][] dp = new int[n + 1][n + 1];
        for (int i = 1; i <= n; ++i) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            for (int j = 1; j <= i; ++j) {
                int num = Integer.parseInt(st.nextToken());
                dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - 1]) + num;
            }
        }
        int mx = 0;
        for (int i = 1; i <= n; ++i) {
            if (dp[n][i] > mx)
                mx = dp[n][i];
        }
        System.out.println(mx);
        br.close();
    }
}