문제

BOJ 9461, 파도반 수열

핵심

• 입력의 크기가 $100$으로 구현에 초점을 맞춘다.
• 정삼각형이 나선 모양으로 추가될 때 n번째 삼각형의 한 변의 길이를 구해야 한다.
  
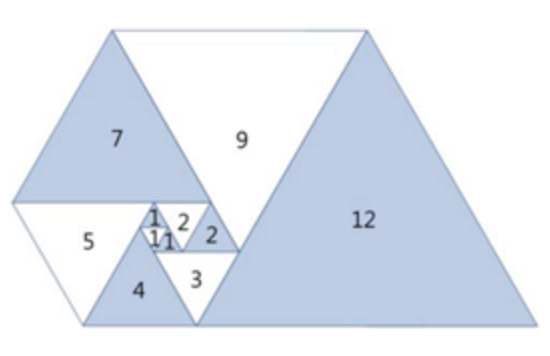
• 일정한 규칙으로 삼각형이 만들어지므로 n번째 삼각형의 길이를 알기 위해 테이블을 만들고 초깃값을 넣어 규칙을 찾아봤다. 그림을 보면 길이가 3인 정삼각형이 만들어지고 나서는 3과 1을 합한 길이가 4인 정삼각형, 4와 1을 합한 길이가 5인 정삼각형, 5와 2를 합한 길이가 7인 정삼각형이 만들어진다.

dp[i]: i번째 정삼각형 한 변의 길이
dp[1] = 1;
dp[2] = 1;   
dp[3] = 1;
dp[4] = 2;   
dp[5] = 2;   
dp[6] = 3;

dp[7] = 4;
dp[8] = 5;
dp[9] = 7;
dp[10] = 9;  
dp[11] = 12

• 규칙을 찾아보면 길이가 3일 때 변이 될 수 있는 원소는 다음과 같았다. {1, 1, 2, 2, 3, 3} 새로운 정삼각형의 길이는 제일 앞에 원소와 제일 뒤의 원소를 더한 값이 된다. 앞 뒤의 원소를 제거하고, 새로운 원소를 2번 추가하면 {1, 2, 2, 3, 4, 4} 새로운 정삼각형 변의 길이를 바로 알 수 있다.
• 앞, 뒤 제거를 효율적으로 하기 위해 deque 자료구조를 사용하였다.

개선

• 위의 풀이보다 더 간단하게 n번째 삼각형 변의 길이는 n - 2번째 삼각형 변의 길이와 n - 3번째 삼각형 변의 길이를 더하면 알 수 있다.

dp[i] = dp[i - 2] + dp[i - 3];

코드

시간복잡도

• $O(N)$

C++

#include <iostream>
#include <deque>
typedef long long ll;
using namespace std;

ll dp[104];
int main(void) {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	dp[1] = 1;
	dp[2] = 1;
	dp[3] = 1;
	dp[4] = 2;
	dp[5] = 2;
	dp[6] = 3;
	deque<ll> seq = {1, 1, 2, 2, 3, 3};
	for (int i = 7; i <= 100; ++i) {
		ll  now = seq.front() + seq.back();
		dp[i] = now;
		seq.pop_front();
		seq.pop_back();
		seq.push_back(now);
		seq.push_back(now);
	}
	int t;
	cin >> t;
	while (t--) {
		int n;
		cin >> n;
		cout << dp[n] << '\n';
	}
}

Java

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        long[] dp = new long[104];
        dp[1] = 1;
        dp[2] = 1;
        dp[3] = 1;
        for (int i = 4; i <= 100; i++)
            dp[i] = dp[i - 2] + dp[i - 3];
        int t = Integer.parseInt(br.readLine());
        while (t-- > 0) {
            int n = Integer.parseInt(br.readLine());
            bw.write(dp[n] + "\n");
        }
        bw.flush();
        bw.close();
        br.close();
    }
}