문제

Programmers Lv3, 등산코스 정하기

핵심

• 여러 개의 출입구와 산봉우리가 주어진다. 출입구에서 산봉우리까지 갔다가 같은 출입구로 되돌아올 때 휴식 없이 이동해야 하는 가장 긴 시간(intensity)이 최소가 되도록 등산 코스를 정해야 한다. 딱 하나의 산봉우리만 거쳐야 한다. 만약 intensity가 최소가 되는 산봉우리가 여러 개라면 산봉우리의 번호가 가장 낮은 코스를 선택한다.
• intensity는 산봉우리에 도착하고 다시 돌아올 때와 같으므로 산봉우리에 도착하기까지 경로만 구하면 된다.
  

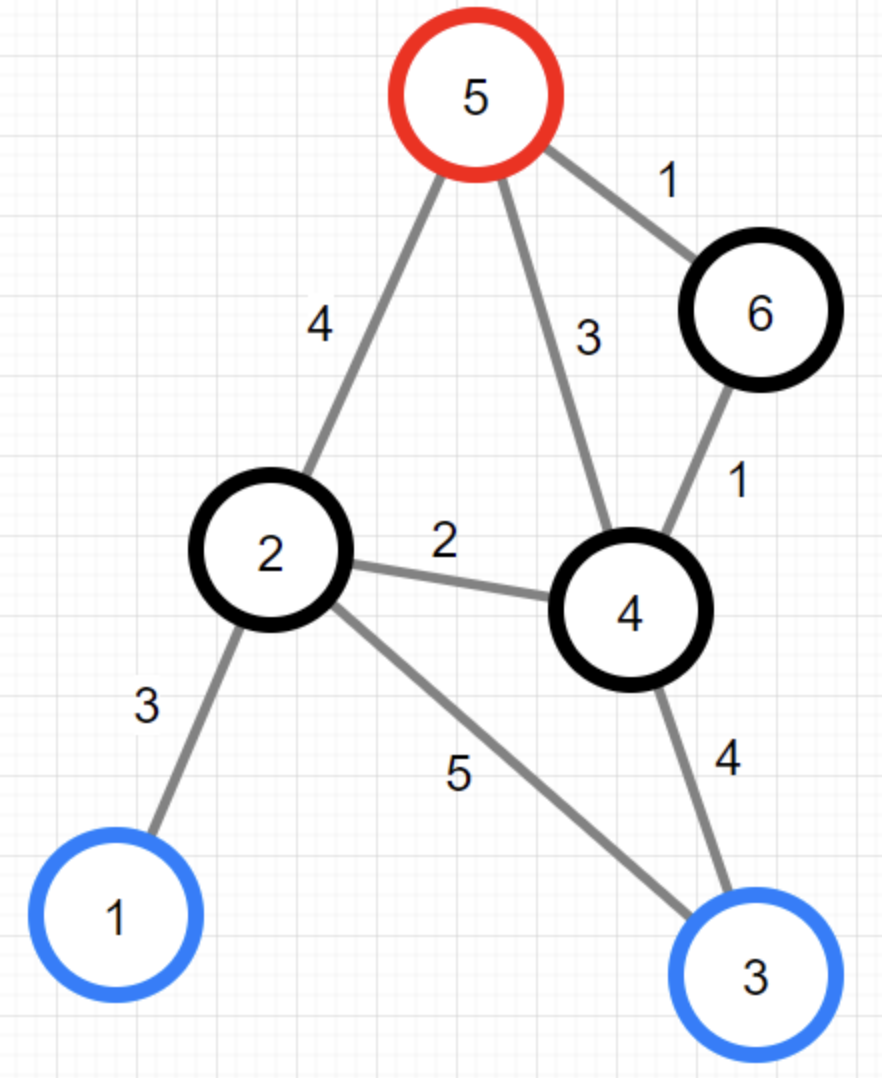
{1, 2, 5}, {1, 2, 4, 5}, {1, 2, 4, 6, 5}
{3, 2, 5}, {3, 2, 4, 5}, {3, 2, 4, 6, 5}, {3, 4, 5}, {3, 4, 6, 5}

• 위 같은 경로가 존재하며 최소 경로와 봉우리는 다음과 같이 존재한다. 해당 예제에선 답이 {5, 3}이 되는 것을 알 수 있다.

{1, 2, 4, 5}, {5} -> 3
{1, 2, 4, 6, 5}, {5} -> 3

다익스트라 알고리즘 (우선순위 큐)

• 출발구에서 산봉우리까지 도착하는 경로를 구하기 위해 다익스트라 알고리즘을 적용할 수 있다. 다익스트라 알고리즘은 특정 정점에서 모든 정점까지의 최단 경로를 구하지만 이를 조금 변형하여 출입구에서 산봉우리까지 최소 intensity를 구할 수 있다.

for (var gate : gates) {
		pq.add(new int[] {0, gate});
		d[gate] = 0;
}

while (!pq.isEmpty()) {
	int[] cur = pq.poll();
	int curWeight = cur[0];
	int curNode = cur[1];

	if (d[curNode] != curWeight) continue; // 이미 거리가 확정된 노드라면 탐색 중지
	if (isSummit(curNode, summits)) continue; // 산봉우리에 도달했을 경우 탐색 중지

	for (var nxt : adj[curNode]) {
		int newWeight = Math.max(curWeight, nxt[0]);
		if (newWeight < d[nxt[1]]) {
			d[nxt[1]] = newWeight;
			pq.add(new int[] {newWeight, nxt[1]});
		}
	}
}

• 문제에서는 최소 intensity가 같을 때 가장 작은 산봉우리 번호를 출력하라 했으므로 아래와 같이 정렬하여 intensity가 같을 때도 가장 작은 산봉우리를 구할 수 있도록 한다. (가장 작은 산봉우리부터 최솟값을 갱신하기에 같은 intensity라면 최솟값 갱신을 생략)

int minSummit = Integer.MAX_VALUE;
int minIntensity = Integer.MAX_VALUE;
Arrays.sort(summits);
for (var s : summits) {
	if (d[s] < minIntensity) {
    	minIntensity = d[s];
        minSummit = s;
    } 
}

개선

시간복잡도

• $O((V+E)logV)$
  

코드

import java.util.*;

class Solution {
    
    public int[] solution(int n, int[][] paths, int[] gates, int[] summits) {
        
        List<int[]>[] adj = new ArrayList[n + 1];
        for (int i = 0; i <= n; ++i) adj[i] = new ArrayList<>();
        
        for (int i = 0; i < paths.length; ++i) {
            adj[paths[i][0]].add(new int[]{paths[i][2], paths[i][1]});
            adj[paths[i][1]].add(new int[]{paths[i][2], paths[i][0]});
        }
        
        int[] d = new int[n + 1];
        Arrays.fill(d, Integer.MAX_VALUE);
        
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> Integer.compare(a[0], b[0]));
        for (var gate : gates) {
            pq.add(new int[] {0, gate});
            d[gate] = 0;
        }

        while (!pq.isEmpty()) {
            int[] cur = pq.poll();
            int curWeight = cur[0];
            int curNode = cur[1];

            if (d[curNode] != curWeight) continue;
            if (isSummit(curNode, summits)) continue;

            for (var nxt : adj[curNode]) {
                int newWeight = Math.max(curWeight, nxt[0]);
                if (newWeight < d[nxt[1]]) {
                    d[nxt[1]] = newWeight;
                    pq.add(new int[] {newWeight, nxt[1]});
                }
            }
        }

        int minSummit = Integer.MAX_VALUE;
        int minIntensity = Integer.MAX_VALUE;
        Arrays.sort(summits);
        for (var s : summits) {
            if (d[s] < minIntensity) {
                minIntensity = d[s];
                minSummit = s;
            } 
        }

        return new int[] {minSummit, minIntensity};
    }
    
    boolean isSummit(int cur, int[] summits) {
        for (var e : summits) if (cur == e) return true;
        return false;
    }
}