문제

Programmers Lv3, 외벽 점검

핵심

• 레스토랑 외벽의 취약한 지점을 최소한의 친구들을 파견해 점검한다. 친구들이 1시간 동안 이동할 수 있는 거리를 주며, 모든 친구를 투입해도 1시간 내 취약 지점을 점검할 수 없으면 -1을 반환한다.
  
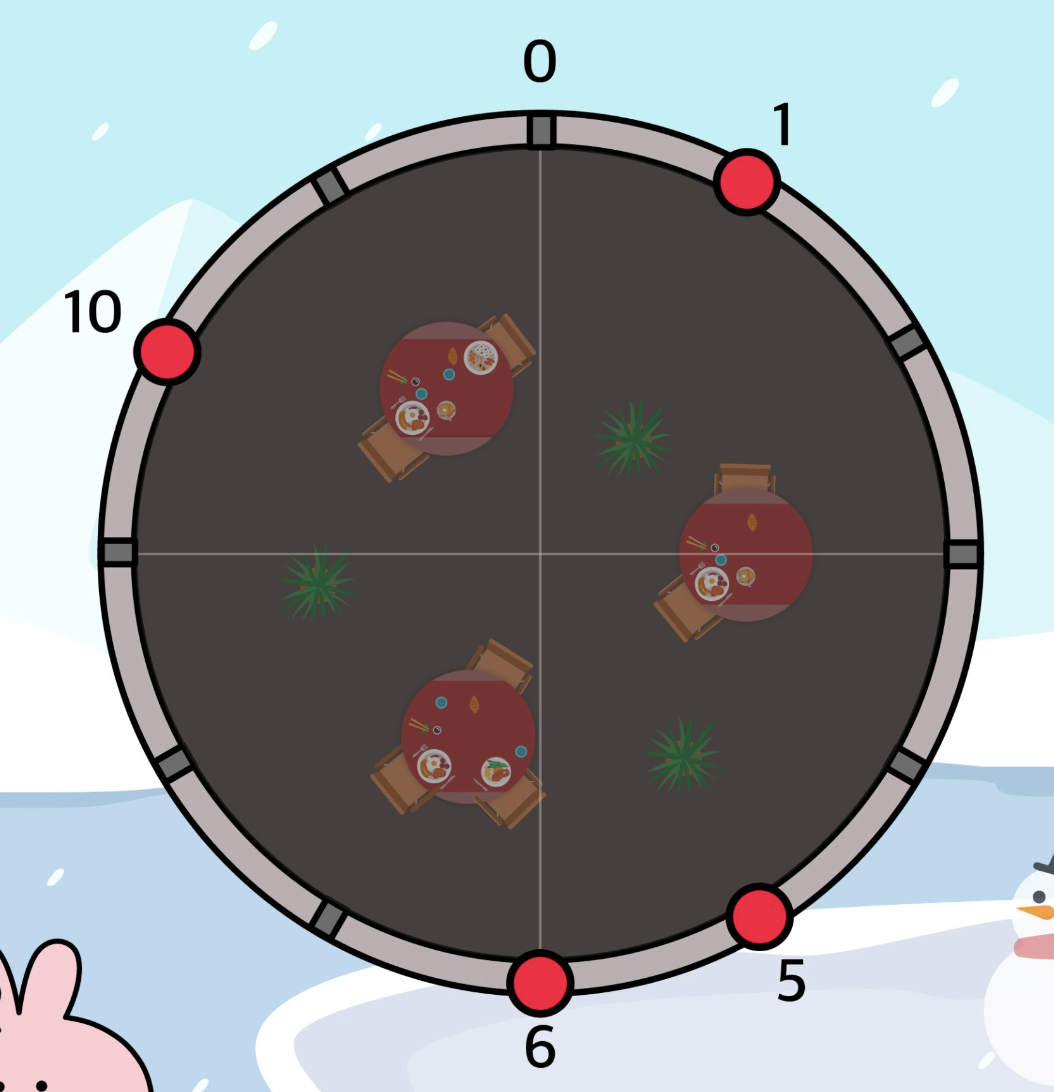
• 취약 지점이 {1,5,6,10}이고, dist가 {1,2,3,4}로 주어졌을 때 4번 친구가 10과 1을 커버하고, 2 또는 3번 친구가 5, 6을 커버한다면 최소 2명으로 모든 취약 지점을 검사할 수 있다.
• n이 200, 취약 지점의 최대 15개, dist가 최대 8개이므로 완전 탐색으로 모든 경우의 수를 구해볼 수 있다. 친구를 배치할 수 있는 모든 순열을 구한 후 각 취약 지점마다 친구를 배치한다. 그런데, 원형이기 때문에 왼쪽 또는 오른쪽으로 갈 수 있는 경우가 생기고 이를 처리하기가 까다롭다.
• 원형을 쭉 늘려서 양방향 탐색을 단방향 탐색으로 간단하게 계산할 수 있다. 문제 예시에서 원판을 시계 방향으로 늘린다고 생각해 보면 {1, 5, 6, 10, 13, 17, 18}의 선형 구조가 된다. 1에서 탐색을 시작하면 10까지, 5에서 탐색을 시작하면 13까지, ... 10에서 탐색을 시작하면 18까지 탐색하면 단방향 탐색만으로 모든 취약 지점을 고려할 수 있다. 이를 코드로 나타내면 아래와 같다.

for (int i = 0; i < weak.length; ++i) weaks.add(weak[i]);
        
for (int i = 0; i < weak.length - 1; ++i) weaks.add(n + weak[i]);

• 친구를 배치하는 모든 순열을 구하고 각 취약 지점에 구한 순열을 배치하면 된다. 시작한 취약 지점으로부터 종료 취약 지점까지 도달하면 되는 것이고, 도달했다면 이때 인원수를 갱신한다.
• 여기서 중요한 처리는 특정 친구가 탐색을 완료했을 때 다음 탐색을 시작한 경로를 구해야 한다. 예를 들어 위의 그림에서 시작점이 6번일 때 종료 지점은 17번이다. 6번에서 거리 1인 친구가 탐색을 완료했다면 다음 지점은 10번 지점이다. 만약 6번에서 거리가 7인 친구가 탐색을 완료했다면 다음 지점은 5가 된다.

// 친구를 배치하는 모든 순열 구하기
for (int i = 0; i < dist.length; ++i) {
	if (isVisited[i]) continue;
	isVisited[i] = true;
	cur.add(dist[i]);
	dfs(cur, isVisited, dist, weaks, w);
	isVisited[i] = false;
	cur.remove(cur.size() - 1);
} 

// 시작한 곳부터 종료한 지점까지, st가 en 이상이라면 모든 취약 지점을 검사했고, 
for (int i = 0; i < w; ++i) {
	int st = weaks.get(i);
	int en = weaks.get(i + w - 1);
	for (int j = 0; j < cur.size(); ++j) {
		st += cur.get(j);
		if (st >= en) {
			int t = j + 1;
			ans = Math.min(ans, j + 1);
			break;
		}
    }
}  

// 다음 시작 지점을 찾는다. 다음 지점보다 더 탐색했었다면, 다다음 지점으로 갱신하는 작업.
for (int k = i + 1; k < i + w; ++k) {
	if (weaks.get(k) > st) {
		st = weaks.get(k);
			break;
	}
}

개선

시간복잡도

• dist 순열 생성: $O(d * d!)$, 친구 배치: $O(w^2 * d)$
• 총 시간 복잡도: $O(d^2 * d! * w^2)$
  

코드

import java.util.*;

public class Solution {
    
    int ans = Integer.MAX_VALUE;
    
    public int solution(int n, int[] weak, int[] dist) {
        List<Integer> weaks = new ArrayList<>();
        
        for (int i = 0; i < weak.length; ++i) weaks.add(weak[i]);
        
        for (int i = 0; i < weak.length - 1; ++i) weaks.add(n + weak[i]);
        
        dfs(new ArrayList<>(), new boolean[dist.length], dist, weaks, weak.length);
        
        return ans == Integer.MAX_VALUE ? -1 : ans;
    }
    
    void dfs(List<Integer> cur, boolean[] isVisited, int[] dist, List<Integer> weaks, int w) {
        
        if (cur.size() == dist.length) {
            for (int i = 0; i < w; ++i) {
                int st = weaks.get(i);
                int en = weaks.get(i + w - 1);
                for (int j = 0; j < cur.size(); ++j) {
                    st += cur.get(j);
                    if (st >= en) {
                        int t = j + 1;
                        ans = Math.min(ans, j + 1);
                        break;
                    }
                    for (int k = i + 1; k < i + w; ++k) {
                        if (weaks.get(k) > st) {
                            st = weaks.get(k);
                            break;
                        }
                    }
                }
            }
            return ;
        }
        for (int i = 0; i < dist.length; ++i) {
            if (isVisited[i]) continue;
            isVisited[i] = true;
            cur.add(dist[i]);
            dfs(cur, isVisited, dist, weaks, w);
            isVisited[i] = false;
            cur.remove(cur.size() - 1);
        }  
    }
}