문제

Programmers Lv3, 산 모양 타일링

핵심

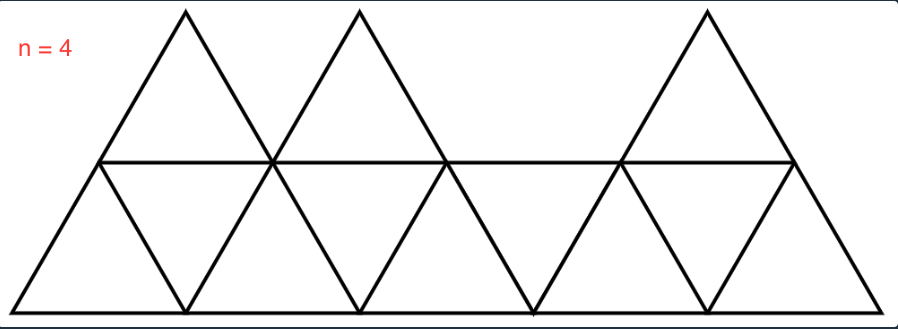
• 한 변의 길이가 1인 정삼각형을 2n+1 개를 이어 붙여 윗변의 길이가 n, 아랫변의 길이가 n+1인 사다리꼴을 만들 수 있다. 이때 사다리꼴 윗변과 변을 공유하는 삼각형을 이어 붙일 수 있다. 이는 tops[] 배열로 주어지며, 1인 경우 삼각형을 이어 붙인 것이다. 이렇게 만든 모양을 삼각형, 마름모 타일을 회전시켜 채워 넣을 수 있다. 채워 넣을 수 있는 방법의 수를 구해야 한다.
  

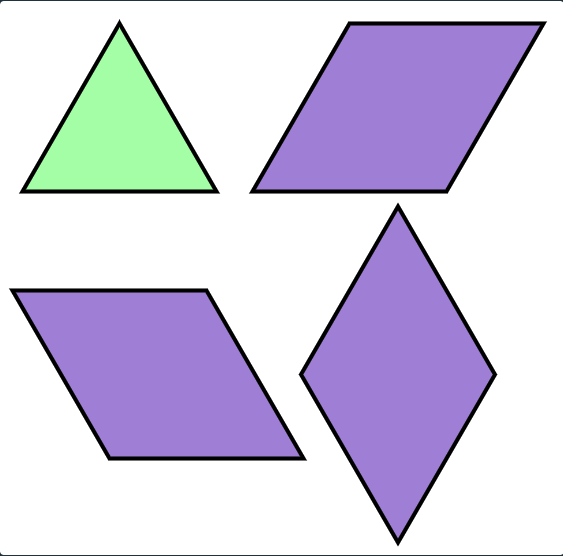
• 채워 넣을 수 있는 타일의 종류
  

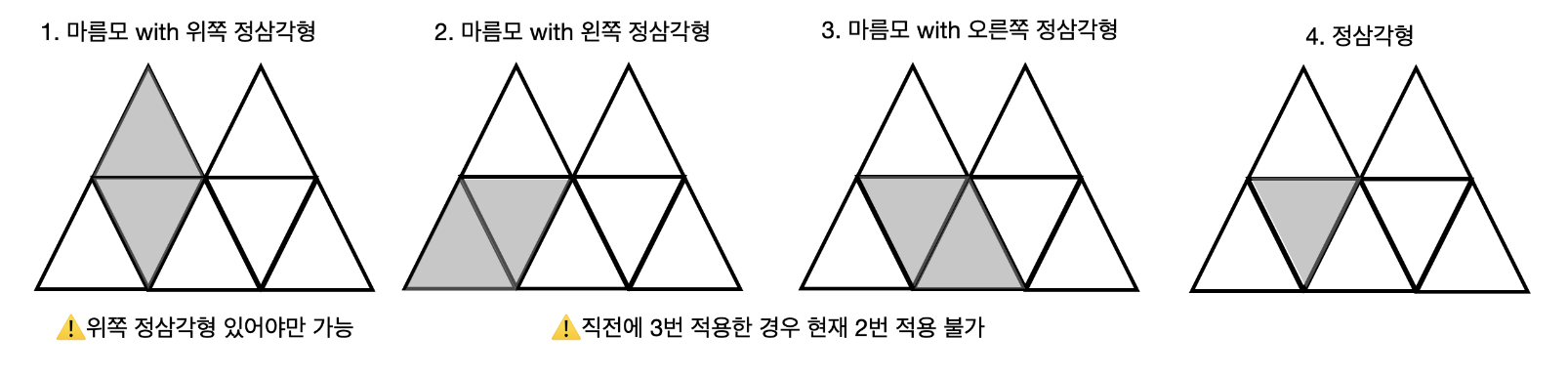
• 점화식을 세울 때 중요한 점은 아래 방향 정삼각형을 기준으로 채울 수 있는 타일의 개수가 결정된다는 점이다. 마름모를 만들 수 있는 경우는 아래 방향 정삼각형을 기준으로 위에 타일을 추가하거나, 왼쪽이나 오른쪽 타일을 추가하거나 또는 아래 방향 정삼각형만 채우는 경우가 존재한다. 그림으로 표현하면 아래와 같다. 나머지 경우는 정삼각형으로 채우면 되기 때문에 별도로 고려하지 않는다.
  

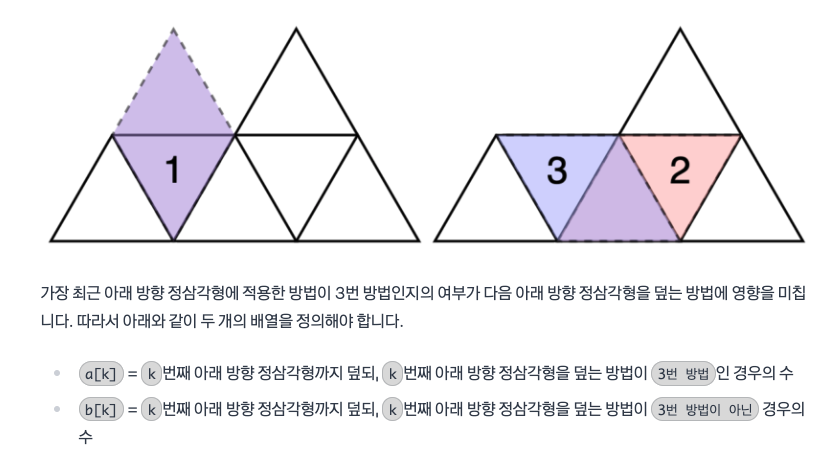
• 왼쪽 정삼각형이랑 합쳐 마름모를 만드는 경우와 오른쪽 정삼각형이랑 합쳐 마름모를 만드는 경우를 중복해서 세면 안 되므로, 이를 각각 개수를 파악해야 한다. 전체 타일을 채우는 경우의 수는 오른쪽 정삼각형을 합쳐 만드는 경우의 수와 오른쪽 정삼각형을 합쳐서 만들지 않는 경우의 수를 더하여 구할 수 있다.
  

• $a[k]$는 k-1 번째 아래 방향 정삼각형이 오른쪽 타일과 합쳤더라도 k번째에도 오른쪽 정삼각형 타일과 합쳐서 만들 수 있다. 위쪽 정삼각형 여부에 상관없이 $a[k] = a[k-1] + b[k-1]$로 구할 수 있다.

• $b[k]$는 위쪽 정삼각형 타일이 붙었다면, 2가지 경우로 나눌 수 있다. 이전 타일에서 오른쪽 정삼각형 타일을 붙여 마름모를 만들었다면, {위쪽, 정삼각형} 2가지 경우가 존재하고 오른쪽 타일을 사용하지 않았다면 {위쪽, 왼쪽, 정삼각형} 3가지 경우가 존재한다. $b[k] = 2 × a[k-1] + 3 × b[k-1]$

• $b[k]$에서 위쪽 정삼각형 타일이 붙지 않은 경우도 2가지 경우로 나눌 수 있다. 이전 타일에서 오른쪽 정삼각형 타일을 붙여 마름모를 만들었다면 {정삼각형} 1가지 경우가 존재하고, 오른쪽 타일을 사용하지 않았다면 {왼쪽, 정삼각형} 2가지 경우가 존재한다. $b[k] = a[k-1] + 2 × b[k-1]$

• https://tech.kakao.com/posts/610 카카오 풀이를 참고하였다.

개선

시간복잡도

• $O(n)$

코드

class Solution {
    public int solution(int n, int[] tops) {
        int[] a = new int[n + 1];
        int[] b = new int[n + 1];
        int mod = 10_007;
        
        a[0] = 0;
        b[0] = 1;
        for (int i = 1; i <= n; ++i) {
            a[i] = (a[i - 1] + b[i - 1]) % mod;
            if (tops[i - 1] > 0) 
                b[i] = (2 * a[i - 1] + 3 * b[i - 1]) % mod;
            else
                b[i] = (a[i - 1] + 2 * b[i - 1]) % mod;
        }
        
        return (a[n] + b[n]) % mod;
    }
}