Programmers Lv3, 주사위 고르기[Java]

junto·2024년 8월 7일

Algorithms DFS/BFS programmers

programmers

목록 보기

64/66

문제

Programmers Lv3, 주사위 고르기

핵심

A와 B가 n개의 주사위 중 n/2 주사위를 골라 주사위를 모두 굴린 후 나온 수들을 비교하여 점수가 큰 쪽이 이기는 주사위 게임을 한다. 주사위마다 쓰인 수의 구성이 모두 다를 때 A가 자신이 승리할 확률이 가장 높은 주사위를 가져가는 경우를 구해야 한다.
지문을 읽어보면 직관적으로 완전 탐색 문제임을 알 수 있다. A, B가 가져갈 주사위 순서를 구한 뒤 나올 수 있는 점수의 합을 구하여 A가 이길 확률이 가장 높은 주사위 순서를 반환하면 된다.

풀이

주사위 고르는 모든 경우를 구한다. (A, B 각각)
고른 주사위 각각의 순서에 대해 점수 합계를 구한 뒤 A가 이기는 횟수를 구한다. 전체 경우의 수는 같고, 무승부와 패배는 고려할 필요 없다.
A가 가장 크게 이길 때 주사위 순서쌍을 오름차순으로 반환한다.

1. 주사위 고르는 모든 경우

dfs를 이용해 모든 순열을 구할 수 있다. 처음엔 아래와 같이 작성했지만, 시간 초과가 발생했다. 이 부분은 아래에서 설명할 예정인데, 어디에서 개선할 수 있는지 잠깐 고민해 보자.

boolean[] isVisited = new boolean[n];
List<int[]> dices = new ArrayList<>();

void dfs(int depth, int[] cur, int n, boolean[] isVisited, List<int[]> dices) {
	if (depth == n / 2) {
		dices.add(cur.clone());
		return;
	}
	
	for (int i = 0; i < n; i++) {
		if (!isVisited[i]) {
			isVisited[i] = true;
			cur[depth] = i;
			dfs(depth + 1, cur, n, isVisited, dices);
			isVisited[i] = false;
		}
	}
}

이렇게 하면 주사위가 {1,2,3,4} 4개가 있을 때 아래와 같은 순열을 만들 수 있다.

A주사위가 0번, 1번 주사위를 선택했을 때 B는 2번 3번 주사위를 선택해야 하므로 전체 {0, 1, 2, 3}을 Set에 담고, A가 가지고 있지 않는 번호는 B에 추가하여 A주사위와 B 주사위를 만들어주었다.

for (var d : dices) {
	Set<Integer> s = new HashSet<>();
	for (int i = 0; i < d.length; ++i) {
		s.add(d[i]);
	}
	List<int[]> aDice = new ArrayList<>();
	List<int[]> bDice = new ArrayList<>();
	
	for (int i = 0; i < n; ++i) {
		if (s.contains(i))
			aDice.add(dice[i]);
		else
			bDice.add(dice[i]);
	}
}

2. 고른 주사위에 대해 A가 이기는 횟수 구하기

위의 과정을 통해 A 주사위와 B주사위에 각각 아래와 같은 값이 들어가 있다.

A (0, 1번 선택)
1 2 3 4 5 6 
3 3 3 3 4 4 

B (2, 3번 선택)
1 3 3 4 4 4 
1 1 4 4 5 5

A, B가 만들 수 있는 점수 합계, 개수를 구한 뒤 A가 B보다 큰 점수 합계에 대해 A 개수 * B 개수를 하면 A가 이기는 횟수를 효율적으로 구할 수 있다. 이를 위해 해쉬맵을 사용한다.

int calculateWin(List<int[]> aDice,  List<int[]> bDice) {
	
	Map<Integer, Integer> aSum = new HashMap<>();
	Map<Integer, Integer> bSum = new HashMap<>();

	dfs2(0, 0, aDice, aSum);
	dfs2(0, 0, bDice, bSum);
	
	int aWinCnt = 0;
	for (var a : aSum.entrySet()) {
		for (var b : bSum.entrySet()) {
			if (a.getKey() > b.getKey()) {
				aWinCnt += (a.getValue() * b.getValue());
			}
		}
	}
	
	return aWinCnt;
}

A, B가 n개의 주사위 중 n/2개를 골라 만들 수 있는 점수 합계와 개수를 구하기 위해 DFS를 사용할 수 있다.

void dfs2(int depth, int sum, List<int[]> dice, Map<Integer, Integer> sums) {
	if (depth == dice.size()) {
		sums.put(sum, sums.getOrDefault(sum, 0) + 1);
		return ;
	}
	for (var score : dice.get(depth)) {
		dfs2(depth + 1, sum + score, dice, sums);
	}
}

3. A가 이전보다 더 크게 이긴 경우 갱신하기

A가 이전보다 더 크게 이겼을 때 주사위 순열까지 함께 갱신한다. 주사위 순열은 오름차순으로 만들어졌으므로 별도로 정렬할 필요는 없다.

if (aWinCnt > max) {
	max = aWinCnt;
	for (int i = 0; i < d.length; ++i) {
		ans[i] = d[i] + 1;
	}
}

개선

위 로직으로 코드를 실행하면 아래와 같이 특정 케이스에서 시간 초과가 난다.

void dfs(int depth, int[] cur, int n, boolean[] isVisited, List<int[]> dices) {
	if (depth == n / 2) {
		dices.add(cur.clone());
		return;
	}
	
	for (int i = 0; i < n; i++) {
		if (!isVisited[i]) {
			isVisited[i] = true;
			cur[depth] = i;
			dfs(depth + 1, cur, n, isVisited, dices);
			isVisited[i] = false;
		}
	}
}

모든 순열을 탐색할 때 매번 0부터 탐색한다. isVisited 배열로 인해 중복 순열이 만들어지지 않지만, 매번 처음부터 탐색하므로 탐색 범위가 넓다.
순열을 만들 때 이전 선택된 것에서 +1 증가한 수를 만들면 되므로 전체를 볼 필요 없이 이전 선택된 것 + 1로 탐색 범위를 좁힐 수 있다. 탐색 범위가 $n!$ 에서 $2^n$ 으로 줄어든다고 볼 수 있다.

int st = depth == 0 ? 0 : cur[depth - 1] + 1; 
for (int i = 0; i < n; i++) {
}

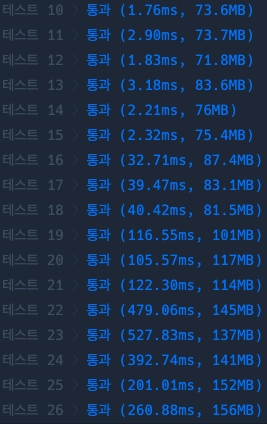
시간복잡도

$O(2^n * 6^n)$

코드

import java.util.*;

class Solution {
    public int[] solution(int[][] dice) {
        int n = dice.length;
        
        boolean[] isVisited = new boolean[n];
        List<int[]> dices = new ArrayList<>();
        
        dfs(0, new int[n / 2], n, isVisited, dices);
        
        int[] ans = new int[n / 2];
        int max = -1;
        for (var d : dices) {
            Set<Integer> s = new HashSet<>();
            for (int i = 0; i < d.length; ++i) {
                s.add(d[i]);
            }
            List<int[]> aDice = new ArrayList<>();
            List<int[]> bDice = new ArrayList<>();
            
            for (int i = 0; i < n; ++i) {
                if (s.contains(i))
                    aDice.add(dice[i]);
                else
                    bDice.add(dice[i]);
            }

            int aWinCnt = calculateWin(aDice, bDice);
            
            if (aWinCnt > max) {
                max = aWinCnt;
                for (int i = 0; i < d.length; ++i) {
                    ans[i] = d[i] + 1;
                }
            }
        }
        
        return ans;
     }
    
     void dfs(int depth, int[] cur, int n, boolean[] isVisited, List<int[]> dices) {
        if (depth == n / 2) {
            dices.add(cur.clone());
            return;
        }
        
        int st = depth == 0 ? 0 : cur[depth - 1] + 1; 
        for (int i = st; i < n; i++) {
            if (!isVisited[i]) {
                isVisited[i] = true;
                cur[depth] = i;
                dfs(depth + 1, cur, n, isVisited, dices);
                isVisited[i] = false;
            }
        }
    }
    
    int calculateWin(List<int[]> aDice,  List<int[]> bDice) {
        
        Map<Integer, Integer> aSum = new HashMap<>();
        Map<Integer, Integer> bSum = new HashMap<>();

        dfs2(0, 0, aDice, aSum);
        dfs2(0, 0, bDice, bSum);
        
        int aWinCnt = 0;
        for (var a : aSum.entrySet()) {
            for (var b : bSum.entrySet()) {
                if (a.getKey() > b.getKey()) {
                    aWinCnt += (a.getValue() * b.getValue());
                }
            }
        }
        
        return aWinCnt;
    }
    
    void dfs2(int depth, int sum, List<int[]> dice, Map<Integer, Integer> sums) {
        if (depth == dice.size()) {
            sums.put(sum, sums.getOrDefault(sum, 0) + 1);
            return ;
        }
        for (var score : dice.get(depth)) {
            dfs2(depth + 1, sum + score, dice, sums);
        }
    }
}