문제

Programmers Lv3, 카드 짝 맞추기

핵심

• 게임 진행 중 카드의 짝을 맞춰 몇 장 제거된 상태에서 카드 앞면의 그림을 알고 있다면, 남은 카드를 모두 제거하는 데 필요한 키 조작 횟수의 최솟값을 구해야 한다. 같은 그림을 제거하지 않으면, 다시 원상 복귀되므로 같은 그림을 먼저 제거하는 방식으로 구해야 최솟값을 구할 수 있다. 1~3번 그림 중 어떤 그림을 먼저 제거하느냐에 따라 움직여야 하는 횟수가 달라지며, 1번을 먼저 지운다고 했을 때 아래 그림처럼 (0,0)을 먼저 지우는지 또는 (3, 2)를 먼저 지우는지에 따라 움직이는 횟수가 다르다.

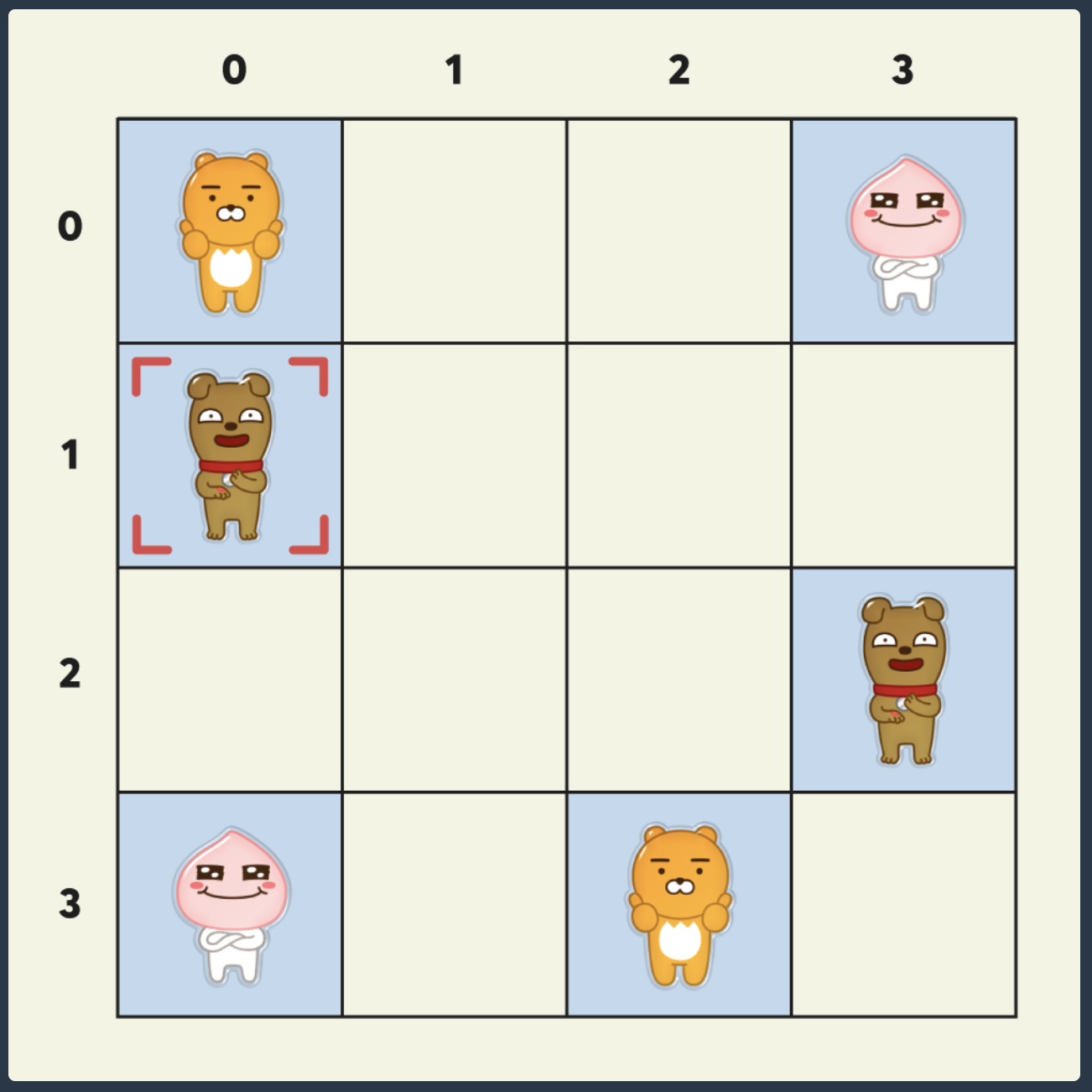
• 즉, 최소 횟수 움직임을 구하기 위해 DFS로 가능한 순열을 만든다. 아래 그림에선 아래와 같은 전체 순열을 만들어야 한다. 가능한 카드 쌍은 최대 3개이며(3!), 카드 쌍마다 순서를 변경할 수 있으므로($2^3$) 총 48가지가 나온다.

0 0, 3 2, 1 0, 2 3, 0 3, 3 0
0 0, 3 2, 1 0, 2 3, 3 0, 0 3
0 0, 3 2, 2 3, 1 0, 0 3, 3 0
0 0, 3 2, 2 3, 1 0, 3 0, 0 3
0 0, 3 2, 0 3, 3 0, 1 0, 2 3
0 0, 3 2, 0 3, 3 0, 2 3, 1 0
0 0, 3 2, 3 0, 0 3, 1 0, 2 3
0 0, 3 2, 3 0, 0 3, 2 3, 1 0 

...

• 위의 순열은 아래와 같은 코드로 만들 수 있다.

void dfs(List<int[]> cur, List<int[]> cards, boolean[] isVisited, List<List<int[]>> perms) {
	if (cur.size() == cards.size()) {
		perms.add(new ArrayList<>(cur));
		return;
	}
	
	for (int i = 0; i < cards.size(); i += 2) {
		if (!isVisited[i]) {
			isVisited[i] = true;
			cur.add(cards.get(i));
			cur.add(cards.get(i + 1));
			dfs(cur, cards, isVisited, perms);
			cur.remove(cur.size() - 1);
			cur.remove(cur.size() - 1);
				
			cur.add(cards.get(i + 1));
			cur.add(cards.get(i));
			dfs(cur, cards, isVisited, perms);
			cur.remove(cur.size() - 1);
			cur.remove(cur.size() - 1);
				
			isVisited[i] = false;
		}
	}
}

• 물론 DFS로 순열을 만들기 전에 같은 그림에 해당하는 좌표를 모으는 작업을 해주어야 한다.

List<int[]> cards = new ArrayList<>();
Map<Integer, List<int[]>> cardPos = new HashMap<>();
for (int i = 0; i < 4; i++) {
	for (int j = 0; j < 4; j++) {
		if (board[i][j] > 0) {
			cardPos.putIfAbsent(board[i][j], new ArrayList<>());
			cardPos.get(board[i][j]).add(new int[]{i, j});
		}
	}
}

for (var pos : cardPos.values()) {
	cards.add(pos.get(0));
	cards.add(pos.get(1));
}

• 가능한 경로를 모두 계산했다면, 각 경로에 대해 최소 움직임 횟수를 구해야 한다. 이는 BFS로 구할 수 있으며, 기존 BFS와 다르게 상하좌우 한 칸씩 이동하는 로직에 더해 한 번에 끝으로 이동하는 로직을 추가해야 한다.

int getMinimumMove(int[][] board, int r, int c, List<int[]> perm) {
	int[][] tmp = new int[4][4];
	for (int i = 0; i < 4; i++) {
		System.arraycopy(board[i], 0, tmp[i], 0, 4);
	}
	
	int move = 0;
	int cr = r;
	int cc = c;
	for (int i = 0; i < perm.size(); i += 2) { // 각 경로에 도착하기 까지
		int[] firstCard = perm.get(i);
		int[] secondCard = perm.get(i + 1);
		
		int firstMove = bfs(tmp, cr, cc, firstCard[0], firstCard[1]); // 현재 경로에서 첫 번째 카드 위치까지
		int secondMove = bfs(tmp, firstCard[0], firstCard[1], secondCard[0], secondCard[1]); // 첫 번째 카드 위치에서 두 번째 카드 위치까지
		
		move += firstMove + secondMove + 2; // 엔터 두번 추가
		tmp[firstCard[0]][firstCard[1]] = 0;
		tmp[secondCard[0]][secondCard[1]] = 0;
		
		cr = secondCard[0];
		cc = secondCard[1];
	}
	
	return move;
}

int bfs(int[][] board, int sy, int sx, int ey, int ex) {
	if (sy == ey && sx == ex) {
		return 0;
	}
	
	Queue<int[]> q = new LinkedList<>();
	boolean[][] isVisited = new boolean[4][4];
	q.add(new int[]{sy, sx, 0});
	isVisited[sy][sx] = true;
	
	while (!q.isEmpty()) {
		int[] cur = q.poll();
		int y = cur[0];
		int x = cur[1];
		int cnt = cur[2];
		
		for (int i = 0; i < 4; i++) {
			int ny = y + dy[i];
			int nx = x + dx[i];
			if (!isOOB(ny, nx) && !isVisited[ny][nx]) {
				if (ny == ey && nx == ex) {
					return cnt + 1;
				}
				isVisited[ny][nx] = true;
				q.add(new int[]{ny, nx, cnt + 1});                 
			}
			
			ny = y;
			nx = x;            
            // 처음 위치에서 한 방향으로 끝에 도달하는 경우
			while (!isOOB(ny + dy[i], nx + dx[i])) {
				ny += dy[i];
				nx += dx[i];
				if (board[ny][nx] != 0) {
						break;
				}
			}
			if (!isVisited[ny][nx]) {
				if (ny == ey && nx == ex) {
					return cnt + 1;
				}
				isVisited[ny][nx] = true;
				q.add(new int[]{ny, nx, cnt + 1});
			}
		}
	}
	
	return Integer.MAX_VALUE;
}

개선

시간복잡도

• $O(V + E)$ (나머지 상수시간)
  

코드

import java.util.*;

class Solution {
    int[] dy = {-1, 0, 1, 0};
    int[] dx = {0, 1, 0, -1};
    
    public int solution(int[][] board, int r, int c) {
        List<int[]> cards = new ArrayList<>();
        Map<Integer, List<int[]>> cardPos = new HashMap<>();
        
        for (int i = 0; i < 4; i++) {
            for (int j = 0; j < 4; j++) {
                if (board[i][j] > 0) {
                    cardPos.putIfAbsent(board[i][j], new ArrayList<>());
                    cardPos.get(board[i][j]).add(new int[]{i, j});
                }
            }
        }
        
        for (var pos : cardPos.values()) {
            cards.add(pos.get(0));
            cards.add(pos.get(1));
        }
        
        List<List<int[]>> perms = new ArrayList<>();
        boolean[] visited = new boolean[cards.size()];
        dfs(new ArrayList<>(), cards, visited, perms);
        
        int ans = Integer.MAX_VALUE;

        for (var perm : perms) {
            ans = Math.min(ans, getMinimumMove(board, r, c, perm));
        }
        
        return ans;
    }
    
   void dfs(List<int[]> cur, List<int[]> cards, boolean[] isVisited, List<List<int[]>> perms) {
        if (cur.size() == cards.size()) {
            perms.add(new ArrayList<>(cur));
            return;
        }
        
        for (int i = 0; i < cards.size(); i += 2) {
            if (!isVisited[i]) {
                isVisited[i] = true;
                cur.add(cards.get(i));
                cur.add(cards.get(i + 1));
                dfs(cur, cards, isVisited, perms);
                cur.remove(cur.size() - 1);
                cur.remove(cur.size() - 1);
                
                cur.add(cards.get(i + 1));
                cur.add(cards.get(i));
                dfs(cur, cards, isVisited, perms);
                cur.remove(cur.size() - 1);
                cur.remove(cur.size() - 1);
                
                isVisited[i] = false;
            }
        }
    }
    
    int getMinimumMove(int[][] board, int r, int c, List<int[]> perm) {
        int[][] tmp = new int[4][4];
        for (int i = 0; i < 4; i++) {
            System.arraycopy(board[i], 0, tmp[i], 0, 4);
        }
        
        int move = 0;
        int cr = r;
        int cc = c;
        
        for (int i = 0; i < perm.size(); i += 2) {
            int[] firstCard = perm.get(i);
            int[] secondCard = perm.get(i + 1);
            
            int firstMove = bfs(tmp, cr, cc, firstCard[0], firstCard[1]);
            int secondMove = bfs(tmp, firstCard[0], firstCard[1], secondCard[0], secondCard[1]);
            
            move += firstMove + secondMove + 2; 
            tmp[firstCard[0]][firstCard[1]] = 0;
            tmp[secondCard[0]][secondCard[1]] = 0;
            
            cr = secondCard[0];
            cc = secondCard[1];
        }
        
        return move;
    }
    
    int bfs(int[][] board, int sy, int sx, int ey, int ex) {
        if (sy == ey && sx == ex) {
            return 0;
        }
        
        Queue<int[]> q = new LinkedList<>();
        boolean[][] isVisited = new boolean[4][4];
        q.add(new int[]{sy, sx, 0});
        isVisited[sy][sx] = true;
        
        while (!q.isEmpty()) {
            int[] cur = q.poll();
            int y = cur[0];
            int x = cur[1];
            int cnt = cur[2];
            
            for (int i = 0; i < 4; i++) {
                int ny = y + dy[i];
                int nx = x + dx[i];
                if (!isOOB(ny, nx) && !isVisited[ny][nx]) {
                    if (ny == ey && nx == ex) {
                        return cnt + 1;
                    }
                    isVisited[ny][nx] = true;
                    q.add(new int[]{ny, nx, cnt + 1});                 
                }
                
                ny = y;
                nx = x;
                while (!isOOB(ny + dy[i], nx + dx[i])) {
                    ny += dy[i];
                    nx += dx[i];
                    if (board[ny][nx] != 0) {
                        break;
                    }
                }
                if (!isVisited[ny][nx]) {
                    if (ny == ey && nx == ex) {
                        return cnt + 1;
                    }
                    isVisited[ny][nx] = true;
                    q.add(new int[]{ny, nx, cnt + 1});
                }
            }
        }
        
        return Integer.MAX_VALUE;
    }
    
    boolean isOOB(int r, int c) {
        return r < 0 || r >= 4 || c < 0 || c >= 4;
    }
}