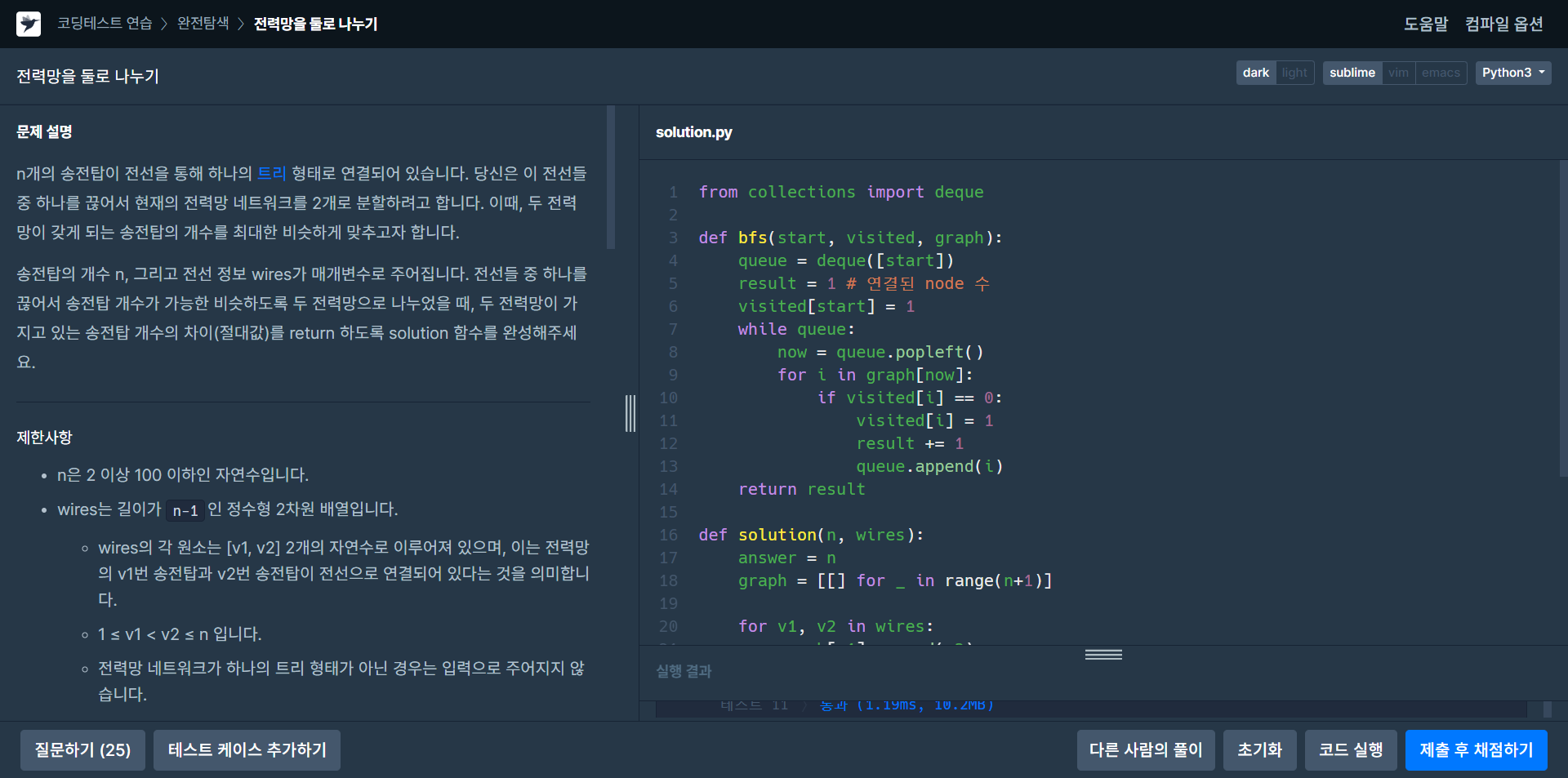
그래프 순회(완전탐색)

👉🏻문제 링크👈🏻

간선의 배열이 주어졌을 때 인접 리스트 생성
인접리스트(Adjacent List) - 각 정점마다 해당 정점으로 나가는 간선의 정보를 저장

graph = [[] for _ in range(n+1)]

for v1, v2 in wires:
    graph[v1].append(v2)
    graph[v2].append(v1)
    
# graph = [[], [3], [3], [1, 2, 4], [3, 5, 6, 7], [4], [4], [4, 8, 9], [7], [7]]

BFS(Breadth First Search)

• 너비우선탐색은 탐색 시작점의 인접한 정점들을 먼저 모두 차례로 방문한 후에, 방문했던 정점을 시작점으로 하여 다시 인접한 정점들을 차례로 방문하는 방식
• 인접한 정점들에 대해 탐색을 한 후, 차례로 다시 너비우선탐색을 진행해야 하므로, 선입선출 형태의 자료구조인 큐를 활용함

BFS 동작 방식

BFS(G, v) // 그래프 G, 탐색 시작점 v
	큐 생성
    시작점 v를 큐에 삽입
    점 v를 방문한 것으로 표시
    while 큐가 비어있지 않은 경우:
    	t <- 큐의 첫번째 원소 반환
        for t와 연결된 모든 선에 대해
        	u <- t의 이웃점
            u가 방문되지 않은 곳이면,
            u를 큐에 넣고, 방문한 것으로 표시

문제 풀이

from collections import deque

def bfs(start, visited, graph):
    queue = deque([start])
    result = 1 # 연결된 node 수
    visited[start] = 1
    while queue:
        now = queue.popleft()
        for i in graph[now]:
            if visited[i] == 0:
                visited[i] = 1
                result += 1
                queue.append(i)
    return result

def solution(n, wires):
    answer = n
    graph = [[] for _ in range(n+1)]
    
    for v1, v2 in wires:
        graph[v1].append(v2)
        graph[v2].append(v1)
    
    for start, not_visit in wires:
        visited = [0] * (n+1)
        visited[not_visit] = 1 # 방문하지 못하도록
        result = bfs(start, visited, graph)
        if answer > abs(n - 2 * result):
            answer = abs(n - 2 * result)
            
    return answer

DFS (Depth First Search)

• 시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색해 가다가 더 이상 갈 곳이 없게 되면, 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아와서 다른 방향의 정점으로 탐색을 계속 반복하여 결국 모든 정점을 방문하는 순회방법
• 가장 마지막에 만났던 갈림길의 정점으로 되돌아가서 다시 깊이 우선 탐색을 반복해야 하므로 후입선출 구조의 스택 사용

DFS 동작 방식

DFS(G, v)
	visited[v] <- True // v 방문 설정
    
    for each all w in adjacency(G, v)
    	if visited[w] != true
        	DFS(G, w)

문제 풀이

from collections import deque

def dfs(v, visited, graph, result):
    result += 1 # 연결된 node 수
    visited[v] = 1
    for w in graph[v]:
        if visited[w] == 0:
            result = dfs(w, visited, graph, result)
    return result

def solution(n, wires):
    answer = n
    graph = [[] for _ in range(n+1)]
    
    for v1, v2 in wires:
        graph[v1].append(v2)
        graph[v2].append(v1)
    
    for start, not_visit in wires:
        visited = [0] * (n+1)
        visited[not_visit] = 1 # 방문하지 못하도록
        result = dfs(start, visited, graph, 0)
        if answer > abs(n - 2 * result):
            answer = abs(n - 2 * result)
            
    return answer